Примеры сочетания: 4.2.3. Сочетания

15.09.1981 alexxlab

Содержание

4.2.3. Сочетания

Глава 4. Комбинаторика

4.2.

4.2.3.

Допустим теперь, что нас не интересует порядок, в котором идут выбранные элементы. Например, нужно из десяти человек выбрать троих дежурных. Такая операция называется неупорядоченной выборкой, или сочетанием, в отличие от упорядоченной выборки – размещений.


	Всякая неупорядоченная выборка объёма k из множества, состоящего из n элементов, (k ≤ n) называется сочетанием из n элементов по k. Количество сочетаний обозначается и вычисляется по формуле

Символ читается «це из эн по ка».

Формулу для можно получить из следующих соображений.

Из любого набора, содержащего k элементов, можно получить k! перестановок. Поэтому упорядоченных выборок объёма k существует

штук. Значит,

Модель 4.4. Сочетания

Пример 1

Для проведения письменного экзамена нужно составить 3 варианта по 5 задач в каждом. Сколькими способами можно разбить 15 задач на 3 варианта?

Показать решение

Пример 2

Сколькими способами можно разместить 10 различных шаров по 4 ящикам так, чтобы в первом ящике оказалось 2 шара, во втором – 3, в третьем – 3 и в четвёртом снова два?

Показать решение

Для числа сочетаний справедливы некоторые тождества, в частности:

Пример 3

Докажите тождество

Показать решение

Запишем в «нулевой» строке число В первой строке напишем значения чисел и каждое из которых тоже равно 1, так, чтобы значение оказалось над промежутком между этими двумя числами. Во второй строке запишем числа и тоже равные 1, а между ними – число Обратим внимание, что число равно сумме двух чисел, стоящих над ним: Продолжим построение, записывая в n-й строке числа от до включительно.

Рисунок 4.2.3.1.

Треугольник Паскаля

Полученный числовой треугольник называется треугольником Паскаля. Согласно свойству любое число в этом треугольнике равно сумме двух чисел, расположенных над ним в предыдущей строке.

При помощи треугольника Паскаля удобно доказывать различные комбинаторные тождества.

Пример 4

Доказать, что

Показать решение

На языке множеств утверждение, доказанное в задаче, выглядит по-другому.

Число подмножеств множества из n элементов равно 2ⁿ.

Еще один интересный факт, связанный с треугольником Паскаля, мы приведём здесь без доказательства:

Бином Ньютона

Приведённое тождество называется биномом Ньютона.

Как и в случае с размещениями, существует понятие числа сочетаний с повторениями. Рассмотрим его на следующем примере.

Пример 5

В палитре художника 8 различных красок. Художник берет кистью наугад любую из красок и ставит цветное пятно на ватмане.

Затем берет следующую кисть, окунает её в любую из красок и делает второе пятно по соседству. Сколько различных комбинаций существует для шести пятен? Порядок пятен на ватмане не важен.

Показать решение

Вообще, можно сформулировать следующее правило.


	Если из множества, содержащего n элементов, выбирается поочередно m элементов, причём выбранный элемент каждый раз возвращается обратно, то количество способов произвести неупорядоченную выборку – число сочетаний с повторениями – составляет

Главная Онлайн учебники База репетиторов России Тренажеры по математике Подготовка к ЕГЭ 2017 онлайн

Адвокат допрос по уголовному делу

в уголовных делах.

Обвиняемому, потерпевшему, свидетелям

zabolotnyy.ru

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: online подготовка к ЕГЭ на College.ru, библиотека ЭОРов и обучающие программы на Multiring.ru.

Сочетания и их свойства примеры. Элементы комбинаторики

КОМБИНАТОРИКА

Комбинаторика — раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.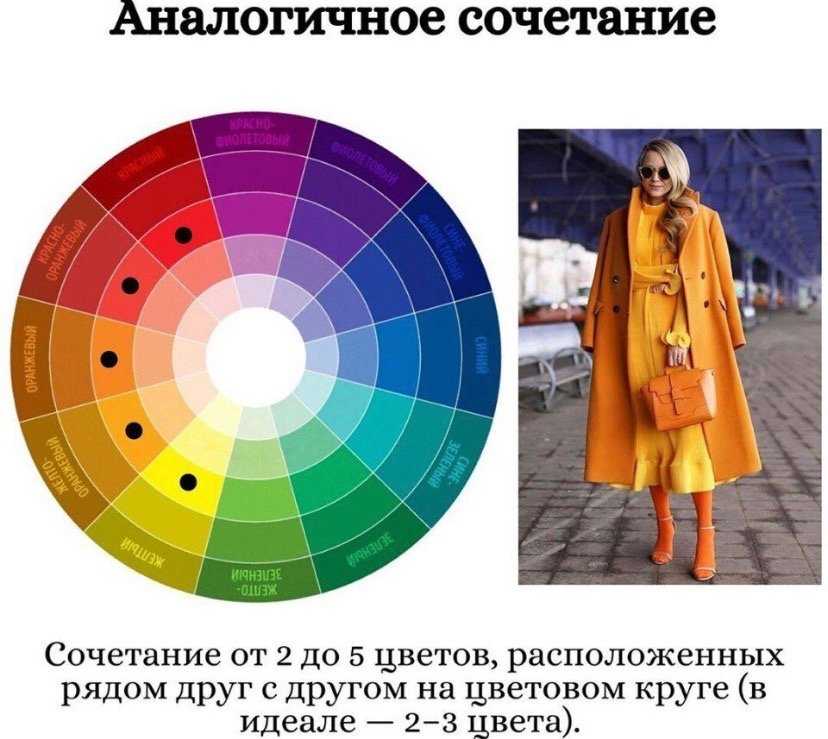

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В — n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Решение

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье — n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:

способами.

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Решение

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Решение

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Решение

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

Решение.

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно вы б рать и разместить по m различным местам m из n предметов, с реди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера- составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Перестановки без повторений . Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Решение

Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k

Пример 8.

Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Решение

Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно

ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»

Комбинаторикой называется раздел математики, изучающий вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).

Правило умножения (основная формула комбинаторики)

Общее число способов, которыми можно выбрать по одному элементу из каждой группы и расставить их в определенном порядке (то есть получить упорядоченную совокупность ), равно:

Пример 1

Монету подбросили 3 раза. Сколько различных результатов бросаний можно ожидать?

Решение

Первая монета имеет альтернативы – либо орел, либо решка. Для второй монеты также есть альтернативы и т.д., т.е. .

Искомое количество способов:

Правило сложения

Если любые две группы и не имеют общих элементов, то выбор одного элемента или из , или из , …или из можно осуществить способами.

Пример 2

На полке 30 книг, из них 20 математических, 6 технических и 4 экономических. Сколько существует способов выбора одной математической или одной экономической книги.

Решение

Математическая книга может быть выбрана способами, экономическая — способами.

По правилу суммы существует способа выбора математической или экономической книги.

Размещения и перестановки

Размещения – это упорядоченные совокупности элементов, отличающиеся друг от друга либо составом, либо порядком элементов.

Размещения без повторений , когда отобранный элемент перед отбором следующего не возвращается в генеральную совокупность. Такой выбор называется последовательным выбором без возвращения, а его результат – размещением без повторений из элементов по .

Число различных способов, которыми можно произвести последовательный выбор без возвращения элементов из генеральной совокупности объема , равно:

Пример 3

Расписание дня состоит из 5 различных уроков. Определите число вариантов расписания при выборе из 11 дисциплин.

Решение

Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов как составом, так и порядком следования. поэтому:

Перестановки – это упорядоченные совокупности, отличающиеся друг от друга только порядком элементов. Число всех перестановок множества из элементов равно

Пример 4

Сколькими способами можно рассадить 4 человек за одним столом?

Решение

Каждый вариант рассадки отличается только порядком участников, то есть является перестановкой из 4 элементов:

Размещения с повторениями , когда отобранный элемент перед отбором следующего возвращается в генеральную совокупность. Такой выбор называется последовательным выбором с возвращением, а его результат — размещением с повторениями из элементов по .

Общее число различных способов, которыми можно произвести выбор с возвращением элементов из генеральной совокупности объема , равно

Пример 5

Лифт останавливается на 7 этажах. Сколькими способами могут выйти на этих этажах 6 пассажиров, находящихся в кабине лифта?

Решение

Каждый из способов распределения пассажиров по этажам представляет собой комбинацию 6 пассажиров по 7 этажам, отличающуюся от других комбинаций как составом, так и их порядком. Так как одном этаже может выйти как один, так и несколько пассажиров, то одни и те же пассажиры могут повторяться. Поэтому число таких комбинаций равно числу размещений с повторениями из 7 элементов по 6:

Сочетания

Сочетаниями из n элементов по k называются неупорядоченные совокупности, отличающиеся друг от друга хотя бы одним элементом.

Пусть из генеральной совокупности берется сразу несколько элементов (либо элементы берут последовательно, но порядок их появления не учитывается). В результате такого одновременного неупорядоченного выбора элементов из генеральной совокупности объема получаются комбинации, которые называются сочетаниями без повторений из элементов по .

Число сочетаний из элементов по равно:

Пример 6

В ящике 9 яблок. Сколькими способами можно выбрать 3 яблока из ящика?

Решение

Каждый вариант выбора состоит из 3 яблок и отличается от других только составом, то есть представляет собой сочетания без повторений из 9 элементов:

Количество способов, которыми можно выбрать 3 яблока из 9:

Пусть из генеральной совокупности объема выбирается элементов, один за другим, причем каждый отобранный элемент перед отбором следующего возвращается в генеральную совокупность. При этом ведется запись, какие элементы появились и сколько раз, однако порядок их появления не учитывается. Получившиеся совокупности называются сочетаниями с повторениями из элементов по .

Число сочетаний с повторениями из элементов по :

Пример 7

На почте продают открытки 3 видов. Сколькими способами можно купить 6 открыток?

Это задача на отыскание числа сочетаний с повторениями из 3 по 6:

Разбиение множества на группы

Пусть множество из различных элементов разбивается на групп так, то в первую группу попадают элементов, во вторую — элементов, в -ю группу — элементов, причем . Такую ситуацию называют разбиением множества на группы.

Число разбиений на групп, когда в первую попадают элементов, во вторую — элементов, в k-ю группу — элементов, равно:

Пример 8

Группу из 16 человек требуется разбить на три подгруппы, в первой из которых должно быть 5 человек, во второй – 7 человек, в третьей – 4 человека. Сколькими способами это можно сделать?

Основные правила комбинаторики.

Комбинаторика — это раздел математики, изучающий способы расположения объектов в соответствии со специальными правилами и методы подсчета числа всех возможных способов. Правило умножения. Если некоторый выбор A можно осуществить m способами, а для каждого из них некоторый другой выбор B можно осуществить n способами, то выбор A и B (в указанном порядке) можно осуществить m×n способами. Пример 1. На гору ведут 6 дорог. Сколькими способами можно подняться на гору и спуститься с горы, если подъем и спуск должен быть по разным дорогам? Решение. Дорогу на гору можно выбрать 6-ю способами, так как подъем и спуск должны быть по разным дорогам, то выбрать дорогу для спуска можно 5-ю способами. Тогда по правилу умножения число способов выбора дороги для подъема и спуска равно 6×5=30. Правило сложения. Если некоторый выбор A можно осуществить m способами, а выбор B можно осуществить n способами, то выбор A или B можно осуществить m+n способами. Пример 2. В ящике имеется 6 красных карандашей, 5 синих и 3 простых карандаша. Сколькими способами можно выбрать цветной карандаш? Решение. Цветной карандаш — это красный или синий, следовательно, по правилу сложения число способов выбора цветного карандаша равно 6+5=11. Замечание. Данные правила можно обобщить на большее число выборов. Вопрос. Сколько основных правил комбинаторики существует?

Перестановки.

Определение 1. Множество называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое натуральное число от 1 до n, где n — это число элементов данного множества, причем разным элементам поставлены в соответствие разные числа.

Упорядоченные множества считаются различными, если они отличаются либо своими элементами, либо их порядком. Определение 2. Различные упорядоченные множества, составленные из элементов данного множества, отличающиеся лишь порядком элементов, называются его перестановками. Пример 3. Рассмотрим множество M={a,b,c}. Это множество из трех элементов. Составим его различные перестановки: (a,b,c),(a,c,b),(b,a,c),(b,c,a),(c,a,b),(c,b,a). Получили 6 перестановок. P n — число всех перестановок множества из n элементов.

P n =n! (1), где

n!=1·2·3·…·n (читается «н факториал»). Замечание. 0!=1; (n+1)!=n!·(n+1) . Пример 4. Сколько шестизначных чисел, кратных пяти, можно составить из цифр 0,1,2,3,4,5, при условии, что в числе нет одинаковых цифр? Решение. Числа, кратные пяти(делящиеся на пять), оканчиваются либо на 0, либо на 5. Если последняя цифра числа 0, то остальные цифры можно располагать в любом порядке, получим перестановки из пяти элементов, их P 5 =5!=120. Если на конце 5, то остальные можно расположить P 5 =120 способами, но среди них не подходят те, которые начинаются на 0, так как это будут не шестизначные числа. а пятизначные, данных чисел P 4 =4!=24.Тогда требуемых чисел будет 120+120-24=216.

Вопрос. Сколько существует перестановок из шести элементов?

Ваш ответ : 720

Перестановки с повторениями.

Если взять цифры 1, 2, 3, 4, то из них можно составить 24 перестановки. Но если взять четыре цифры 1, 1, 2, 2, то можно получить только следующие различные перестановки: (1,1,2,2),(1,2,1,2),(1,2,2,1),((2,2,1,1),(2,1,2,1),(2,1,1,2), то есть шесть перестановок, их в 4 раза меньше, чем перестановок из четырех различных чисел, так как перестановки, в которых меняются местами одинаковые числа — это не новые перестановки, их 2!·2!=4. Рассмотрим задачу в общем виде:пусть имеется множество из элементов, в котором элементы встречаются раз, элементы встречаются раз,…, элементы встречаются раз, причем .

Определение 3. Перестановки с повторениями — это перестановки из элементов данного множества, в которых элементы повторяются. — число всех перестановок с повторениями. Число перестановок, не меняющих данную перестановку с повторениями равно , а чисел можно переставлять способами, поэтому получаем следующую формулу для вычисления числа перестановок с повторениями:

Пример 4. Сколькими способами можно расселить 8 студентов по трем комнатам: одноместной, трехместной и четырехместной? Решение. Различныеспособы расселения студентов по комнатам являются перестановками с повторениями, так как внутри, например, трехместной комнаты выбранные студенты могут занимать спальные места по-разному, но эти варианты не будут являться новыми перестановками, поэтому получаем: То есть всего 280 способов расселения студентов. Вопрос. Вычислить

Сочетания.

Пусть некоторое множество содержит n элементов.

Определение 4. Всякое m- элементное подмножество n- элементного множества называется сочетанием из n элементов по m. — число всех сочетаний.

(3)

Пример 5. Для соревнований из 30 спортсменов надо выбрать трех человек. Сколькими способами это можно сделать? Решение. Команда из 3 спортсменов — это подмножество из трех элементов, то есть сочетание из 30 по 3, поэтому количество способов выбора таких команд вычисляется по формуле (3): .

Свойства сочетаний.

1. 2. . Из данных свойств следует, что , тогда , далее , , и так далее. Можно расположить эти числа в виде таблицы:

……………………………………………..

…………………..

Эта таблица в виде треугольника называется треугольником Паскаля.

Определение 5. Выражение a+b называется биномом.

Формула (4) называется биномиальной формулой Ньютона, а коэффициенты называются биномиальными коэффициентами. Из данной формулы вытекает следующее свойство числа сочетаний

Вопрос. .

Сочетания с повторениями

Пусть имеется множество, содержащее n видов элементов, поэтому есть взять какое-то подмножество этого множества, то в нем могут быть одинаковые элементы. Определение 6. Сочетание с повторениями — это m- элементное подмножество множества, содержащего n видов элементов, в котором элементы повторяются. — число всех сочетаний с повторениями из n по m. Состав m- элементного подмножества имеет вид , где . Заменяя каждое из чисел соответствующим количеством единиц и разделяя единицы нулями, получаем набор, состоящий из m единиц и n-1 нулей. Каждому составу отвечает только одна запись из нулей и единиц, а каждая запись задает только один состав, следовательно, число различных составов равно числу перестановок с повторениями из n-1 нулей и m единиц. Получаем формулу для вычисления всех сочетаний с повторениями.

(5)

Пример 6. В кондитерском магазине продаются пирожные четырех видов: наполеоны, эклеры, песочные и бисквитные. Сколькими способами можно купить 7 пирожных? Решение. Любая покупка — это подмножество, в котором могут быть одинаковые элементы, поэтому это сочетание с повторениями. Число всех возможных покупок находим по формуле (5): . Вопрос. В формуле (5) m может быть больше n.

Размещения

Определение 7. Упорядоченное m — элементное подмножество n- элементного множества называется размещением. — число всех размещений из n элементов по m. Число всех размещений из n по m больше числа всех сочетаний из n по m, так как из каждого подмножества из m элементов с помощью перестановок можно получить m! упорядоченных подмножеств, получаем формулу для числа размещений

(6)

Пример 7. В группе 25 человек. Нужно выбрать актив группы: старосту, заместителя старосты и профорга. Сколькими способами это можно сделать? Решение. Актив группы — это упорядоченное подмножество из трех элементов, так как надо выбрать не только трех человек, но и распределить между ними должности, значит актив группы — это размещение, число всех размещений вычисляем по формуле (6): . Вопрос. Во сколько раз число сочетаний из 20 по 4 меньше числа размещений из 20 по 4?

Размещения с повторениями

Пусть дано множество из n элементов, в котором есть одинаковые элементы, тогда его подмножества тоже могут содержать одинаковые элементы. Определение 8. Упорядоченные m- элементные подмножества n- элементного множества, в которых элементы могут повторяться, называются размещениями с повторениями. — число всех размещений из n по m. В подмножестве из m элементов первый элемент можно выбрать n способами(то есть любой элемент множества) , так как элементы могут повторяться, то второй элемент тоже можно выбрать n способами, аналогично остальные элементы подмножества можно выбрать n способами, если воспользоваться правилом умножения, получим формулу для вычисления числа размещений с повторениями:

Пример 8. В лифт десятиэтажного дома вошли 5 человек. Каждый из них может выйти на любом этаже, начиная со второго. Сколькими способами они могут это сделать? Решение. Так как каждый человек может выйти на любом этаже, начиная со второго, то этажей для выхода 9. Надо выбрать этажи для возможности выхода каждого человека: для первого человека — можно выбрать любой из девяти этажей, аналогично для остальных пассажиров, тогда по формуле (7): способов. Вопрос. Вычислить .

При решении многих практических задач приходится использовать комбинации элементов, выбирать из данной совокупности те, которые имеют определенные свойства, и размещать их в определенном порядке. Такие задачи называются комбинаторными . Раздел математики, посвящённый решению задач выбора и расположения элементов в соответствии с данными условиями, называется комбинаторикой. Термин «комбинаторика» происходит от латинского слова «combina» , что в переводе на русский язык означает – «сочетать», «соединять».

Выбранные группы элементов называют соединениями. Если все элементы соединения разные, то получаем соединения без повторений, которые и рассмотрим ниже.

Большинство комбинаторных задач решается с помощью двух основных правил – правила суммы и правила произведения .

Задача 1.

В магазине «Все для чая» есть 6 разных чашек и 4 разных блюдца. Сколько вариантов чашки и блюдца можно купить?

Решение .

Чашку мы можем выбрать 6-ю способами, а блюдце 4-я способами. Так как нам надо купить пару чашку и блюдце, то это можно сделать 6 · 4 = 24 способами (по правилу произведения).

Ответ: 24.

Для успешного решения комбинаторных задач надо еще и правильно выбрать формулу, по которой искать количество нужных соединений. В этом поможет следующая схема.

Рассмотрим решение нескольких задач на разные виды соединений без повторений.

Задача 2.

Найдите количество трехзначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, 7, если цифры в числе повторяться не могут.

Решение.

Для выбора формулы выясняем, что для чисел, которые мы будем составлять, порядок учитывается и не все элементы одновременно выбираются. Значит, это соединение – размещение из 7 элементов по 3. Воспользуемся формулой для числа размещений: A 7 3 = 7(7 – 1)(7 – 2) = 7 · 6 · 5 = 210 чисел.

Ответ: 210.

Задача 3.

Сколько существует семизначных телефонных номеров, в которых все цифры разные, а номер не может начинаться с нуля?

Решение.

На первый взгляд эта задача такая же, как и предыдущая, но сложность в том, что надо не учитывать те соединения, которые начинаются с нуля. Значит необходимо из существующих 10-ти цифр составить все семизначные номера телефонов, а потом от полученного числа отнять количество номеров, начинающихся с нуля. Формула будет иметь вид:

A 10 7 – A 9 6 = 10 · 9 · 8 · 7 · 6 · 5 · 4 – 9 · 8 · 7 · 6 · 5 · 4 = 544 320.

Ответ: 544 320.

Задача 4.

Сколькими способами можно расставить на полке 12 книг, из которых 5 книг – это сборники стихотворений, так, чтобы сборники стояли рядом?

Решение.

Сначала примем 5 сборников условно за одну книгу, потому что они должны стоять рядом. Так как в соединении существенным есть порядок, и все элементы используются, значит это перестановки из 8 элементов (7 книг + условная 1 книга).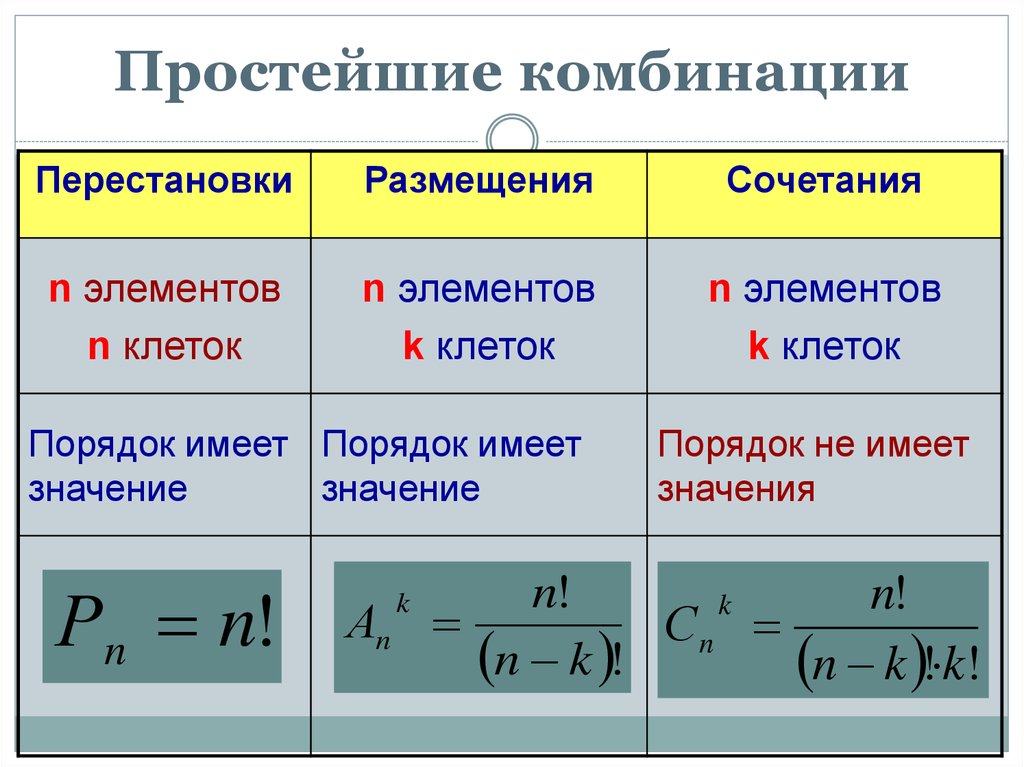 Их количество Р 8 . Далее будем переставлять между собой только сборники стихотворений. Это можно сделать Р 5 способами. Поскольку нам нужно расставить и сборники, и другие книги, то воспользуемся правилом произведения. Следовательно, Р 8 · Р 5 = 8! · 5!. Число способов будет большим, поэтому ответ можно оставить в виде произведения факториалов.

Ответ: 8! · 5!

Задача 5 .

В классе 16 мальчиков и 12 девочек. Для уборки территории возле школы нужно 4 мальчика и 3 девочки. Сколькими способами можно их выбрать со всех учеников класса?

Решение.

Сначала отдельно выберем 4 мальчика из 16 и 3 девочки из 12. Так как порядок размещения не учитывается, то соответственные соединения – сочетания без повторений. Учитывая необходимость одновременного выбора и мальчиков, и девочек, используем правило произведения. В результате число способов будет вычисляться таким образом:

С 16 4 · С 12 3 = (16!/(4! · 12!)) · (12!/(3! · 9!)) = ((13 · 14 · 15 · 16) / (2 · 3 · 4)) ·((10 · 11 · 12) / (2 · 3)) = 400 400.

Ответ: 400 400.

Таким образом, успешное решение комбинаторной задачи зависит от правильного анализа ее условия, определения типа соединений, которые будут составляться, и выбора подходящей формулы для вычисления их количества.

Остались вопросы? Не знаете, как решать комбинаторные задачи?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Комбинаторика: основные правила и формулы.

КОМБИНАТОРИКА

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Решение

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены:

способами.

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Решение

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Решение

Пример 4.

Решение

Размещения без повторений. Размещения с повторениями

Пример 5.

Решение.

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Решение

Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

Перестановки без повторений. Перестановки с повторениями

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Решение

Пример 8.

Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Решение

ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»

СОЧЕТАНИЕ — Что такое СОЧЕТАНИЕ?

Слово состоит из 9 букв: первая с, вторая о, третья ч, четвёртая е, пятая т, шестая а, седьмая н, восьмая и, последняя е,

Слово сочетание английскими буквами(транслитом) — sochetanie

Буква с встречается 1 раз. Слова с 1 буквой с
Буква о встречается 1 раз. Слова с 1 буквой о
Буква ч встречается 1 раз. Слова с 1 буквой ч
Буква е встречается 2 раза. Слова с 2 буквами е
Буква т встречается 1 раз. Слова с 1 буквой т
Буква а встречается 1 раз. Слова с 1 буквой а
Буква н встречается 1 раз. Слова с 1 буквой н
Буква и встречается 1 раз. Слова с 1 буквой и

Значения слова сочетание. Что такое сочетание?

Сочетание

Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
ru.wikipedia.org

СОЧЕТАНИЕ — из тэлементов по п- подмножество мощности пнек-рого исходного конечного множества мощности т. Число С. из тэлементов по и, обозначаемое или равно. Производящая функция для последовательности п = 0, 1,…, т, имеет вид.
Математическая энциклопедия. — 1977-1985

Сочетания в математике, соединения, составленные из n элементов по k элементов в каждой группе и отличающиеся друг от друга хотя бы одним элементом. Число С. из n элементов по k обозначается через Cnk или (nk) и равно n!/k! (n —k)!.
БСЭ. — 1969—1978

СОЧЕТАНИЕ Синтез фонетических элементов. Термин используется для описания аспекта звукового подхода к обучению чтению, относящегося к освоению ребенком звуко-буквенного соответствия и объединения звуков.
Оксфордский словарь по психологии. — 2002

Сочетания

Сочетания — закономерная смена (чередование) п. по мезорельефу. В последнее время С. предлагается называть почвенные комбинации, в которых регулярно чередуются довольно крупные (порядка гектаров и десятка гектаров) ареалы контрастно различающихся п.
Толковый словарь по почвоведению. — 1975

Сочетание клавиш

Сочета́ние кла́виш (синонимы: горячая клавиша, шорткат (англ. shortcut), клавиша быстрого доступа, клавиша быстрого вызова, клавиатурный ускоритель) (англ. keyboard shortcut, quick key, access key, hot key) (для программного обеспечения)…
ru.wikipedia.org

Сочетание знаков препинания

Сочетание знаков препинания Постановка рядом двух знаков препинания внутри предложения на основании действующих правил. История открытий, изобретений, история техники, которая облегчает жизнь и труд людей,— вот собственно история культуры (Горький).
Розенталь Д.Э. Словарь-справочник лингвистических терминов. — 1976

АЛГОРИТМОВ СОЧЕТАНИЯ

АЛГОРИТМОВ СОЧЕТАНИЯ — название, установившееся за рядом конкретных способов конструирования новых алгоритмов из нескольких заданных. В применении к нормальным алгорифмам наибольшую известность получили следующие А. с.
Математическая энциклопедия. — 1977-1985

Трехголосное сочетание

Трехголосное сочетание музыка, написанная для трех партий. В ней применяются преимущественно трехзвучия, аккорды же четырех- и пятизвучные не полностью с пропуском менее существенных нот.
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — 1890-1907

Фразеологическое сочетание

Фразеологическое сочетание — разновидность фразеологической единицы, которая, будучи построена по продуктивной модели, не обладает в отличие от фразеологического единства полной семантической слитностью…
Нелюбин Л.Л. Толковый переводоведческий словарь. — 2003

Таутосиллабаческие сочетания

Таутосиллабаческие сочетания звуков (грамм. ) — термин, изобретенный К. Бругманом и входящий в употребление в научной литературе. Обыкновенно он прилагается к сочетаниям гласных звуков друг с другом, т. е. дифтонгам в тесном смысле слова…
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — 1890-1907

Правила чтения букв и буквенных сочетаний датского языка

Ударный гласный обычно долгий в открытом слоге; в односложных словах, оканчивающихся непосредственно на гласный или на гласный, за которым следует неударный гласный, напр.: træ (дерево), blå (синий), stue (комната), или в словах…Однако если ударный гласный в закрытом слоге находится перед сочетанием согласных, возникшем при склонении, спряжении или словообразовании, то он обычно сохраняет свою долготу, напр.: dag…
ru.wikipedia.org

Русский язык

Сочета́ние, -я.
Орфографический словарь. — 2004

Сочета́/ни/е [й/э].
Морфемно-орфографический словарь. — 2002

Примеры употребления слова сочетание

Но здесь мы видим необычное сочетание мягкой женственности и яркой сексапильности.

Их сочетание в одном матче должно увеличить самоотдачу футболистов в несколько раз.

Утверждал, что всегда исповедовал принцип: люблю сочетание приятного с бесполезным.

Новая модель Touareg Edition X представляет собой безупречное сочетание стиля и технологий.

Риск, в общем случае, является сочетание вероятности и тяжести нештатной ситуации.

Именно такое необычное сочетание металла и поликарбоната должно придать наградам воздушность.

Наше внутреннее содержание и их форма даст эффективное и гармоничное сочетание.

Необычное сочетание металла и поликарбоната придает изделиям воздушность и красоту.

Необычное сочетание металла и поликарбоната придает изделиям воздушность.

Ни одно сочетание, оказавшееся в третьей четверти на паркете, не смогло.

Слова из слова «сочетание»
Слова на букву «с»
Слова, начинающиеся на «со»
Слова c буквой «е» на конце
Слова c «ие» на конце
Слова, начинающиеся на «соч»
Слова, начинающиеся на «соче»
Слова, оканчивающиеся на «ние»
Слова, заканчивающиеся на «ание»

сочетавший
сочетаемость
сочетаемый
сочетание
сочетанный
сочетательный
сочетаться

Пример сочетания клавиш MUI — Win32 apps

Twitter LinkedIn Facebook Адрес электронной почты

Статья
05/11/2022
Чтение занимает 2 мин

В этом разделе описывается, как добавить строки ресурсов в таблицу ярлыков установщика Windows для использования с многоязычными пользовательскими интерфейсами (MUI).

Windows Installer 2.0 и Windows Installer 3.0: не поддерживается. В этом примере требуется Windows Installer 4.0.

Сведения о разработке приложений с поддержкой MUI см. в документации по многоязычный пользовательский интерфейс (MUI).

Чтобы добавить строки ресурсов, используемые многоязычными пользовательскими интерфейсами Windows Vista, в пакет установщика Windows:

Добавьте сведения для всех файлов, не зависящих от языка и языка, в таблицу файлов. Например, файлы могут состоять из файлов с нейтральным языком (msimsg.dll) и языковых файлов для английского языка (msimsgen.dll.mui), японского (msimsgja.dll.mui) и китайского (msimsgcs.dll.mui). Каждый файл может принадлежать к другому компоненту. Каждый файл может иметь как длинное, так и короткое имя файла. В этом примере в таблицу файлов можно добавить следующие сведения.

Таблица файлов (частичная)

Файл	Component_	FileName
msimsgmuija	MSIMSG_MUI_JA	msimsgja. dll\|msimsg.dll.mui
msimsgmuics	MSIMSG_MUI_CS	msimsgcs.dll\|msimsg.dll.mui
msimsgmuien	MSIMSG_MUI_EN	msimsgen.dll\|msimsg.dll.mui
msimsgdll	MSIMSG	msimsg.dll

Добавьте сведения в таблицу компонентов для этих компонентов. Каждый компонент имеет уникальный идентификатор GUID, который следует ввести в поле ComponentId таблицы ComponentId. Файл, принадлежащий компоненту, может служить keyPath для этого компонента. Каталог, содержащий каждый компонент, можно указать в поле Directory_. В таблицу компонентов можно добавить следующие сведения.
Таблица компонентов (частичная)
Компонент Directory_ KeyPath
MSIMSG_MUI_JA MUIFolder_JA msimsgmuija
MSIMSG_MUI_CS MUIFolder_CS msimsgmuics
MSIMSG_MUI_EN MUIFolder_EN msimsgmuien
MSIMSG MUIFolder msimsgdll

Компонент	Directory_	KeyPath
MSIMSG_MUI_JA	MUIFolder_JA	msimsgmuija
MSIMSG_MUI_CS	MUIFolder_CS	msimsgmuics
MSIMSG_MUI_EN	MUIFolder_EN	msimsgmuien
MSIMSG	MUIFolder	msimsgdll

Измените таблицу каталогов , чтобы компоненты были установлены в правильные каталоги. Не забудьте включить сведения о каталоге, в котором будет установлен ярлык. Например, следующие сведения можно добавить в таблицу каталогов пакета, который устанавливает компоненты и ярлык, расположенный в каталоге DesktopFolder.

Таблица каталогов (частичная)

Каталог	Directory_Parent	DefaultDir
TARGETDIR		SourceDir
Msitest	TARGETDIR	Msitest:.
MUIFolder	Msitest	MUI
MUIFolder_CS	MUIFolder	cs-CZ
MUIFolder_EN	MUIFolder	en-US
MUIFolder_JA	MUIFolder	ja-JP
DesktopFolder	TARGETDIR	.

Добавьте строку в таблицу ярлыков для каждого ярлыка. Например, таблица ярлыков может содержать следующие сведения для двух сочетаний клавиш Quick1 и Quick2, установленных в каталог DirectoryFolder. Каждое сочетание клавиш относится к функции, указанной в поле «Целевой». Значок, связанный с ярлыком, можно указать в поле Icon_ и таблице значков .

Таблица ярлыков (частичная)

Сочетание клавиш	Directory_	Component_	Назначение	Значок
Быстрая1	DesktopFolder	MSIMSG	FeatureChild1_Local	HelpFileIcon.exe
Быстрая2	DesktopFolder	MSIMSG	FeatureChild1_Local	HelpFileIcon.exe

Добавление сведений в таблицу «Таблица компонентов » для сочетания клавиш, принадлежащих функции. При активации ярлыка установщик проверяет, установлены ли все компоненты, принадлежащие этой функции, перед запуском файла ключа компонента, указанного в столбце Component_ таблицы ярлыков . В этом примере следующие сведения можно добавить в таблицу «Таблица компонентов» для компонента FeatureParent1_Local.
Таблица компонентов (частичная)
Компонент Feature_Parent Title Атрибуты
FeatureParent1_Local FeatureParent1_Local 16
FeatureChild1_Local FeatureParent1_Local FeatureParent1_Local 0
Для каждого нового ярлыка добавьте сведения о строке ресурса в поля DisplayResourceDLL, DisplayResourceId, DescriptionResourceDLL и DescriptionResourceId таблицы Ярлыков. Поля DisplayResourceDLL и DescriptionResourceDLL содержат строку ресурса в формате отформатированных строк. Форматированная строка может использовать соглашение [#filekey] форматированного формата. Добавьте индексы отображения и описания для строк ресурсов в полях DisplayResourceId и DescriptionResourceId.
Таблица ярлыков (частичная)
Сочетание клавиш DisplayResourceDLL DisplayResourceId DescriptionResourceDLL DescriptionResourceId
Quick1 [#msimsgdll] 36 [#msimsgdll] 37
Быстрый2 [#msimsgdll] 38 [#msimsgdll] 39
После установки пакета проверьте, работает ли многоязычный пользовательский интерфейс должным образом.

Компонент	Feature_Parent	Title	Атрибуты
FeatureParent1_Local		FeatureParent1_Local	16
FeatureChild1_Local	FeatureParent1_Local	FeatureParent1_Local	0

Сочетание клавиш	DisplayResourceDLL	DisplayResourceId	DescriptionResourceDLL	DescriptionResourceId
Quick1	[#msimsgdll]	36	[#msimsgdll]	37
Быстрый2	[#msimsgdll]	38	[#msimsgdll]	39

ТОП-20 лучших цветовых сочетаний | Наглядные примеры

Подбирайте цветовые сочетания в один клик в программе ФотоМАСТЕР!

Скачать Всего 213 Mb Узнать больше

Для Windows 11, 10, 8, 7 и XP. Быстрая установка.

ТОП-20 цветовых сочетаний: описание и примеры

Автор статьи:Евгения Соколова

02.07.2021

Каждый фотограф, художник, дизайнер и ретушер обязан знать как гармонично сочетать оттенки. Красивые цветовые сочетания — это продукт не спонтанного мышления его творца, а система знаний, базирующаяся на концепции круга Иттена. Правильно построенные схемы визуально влияют на зрителя, вызывая различные эмоции и формируя то
или иное настроение. Опираясь на принципы работы с цветом, вы можете выбрать гамму для интерфейса сайта, интерьера комнаты или иллюстрации. Давайте рассмотрим готовые палитры цветов на примерах.

Теплые сочетания

Крокусы

Здесь задействованы родственные спектральные цвета, то есть те, которые стоят на круге Иттена рядом. Такая подборка подойдет, если вам нужны мягкие переходы без резких акцентов. Фотография вызывает общее ощущение теплоты, что приводит к приятному эмоциональному отклику и настраивает на внутренний уют.

Каштан

В этом примере также использована теплая цветовая гамма и аналоговое сочетание цветов: желто-оранжевое,
зелено-оранжевое, коричнево-золотистое. Но в целом картинка смотрится довольно контрастно.

Оформление в стиле Ван-Гога

Гамма из трех основных цветов: красного, оранжевого и бежевого с доминирующей ноткой терракоты. Создает иллюзию защищенности и безопасности, поэтому отлично подойдет для оформления кофеен и шоурума.

Золотые листья

Яркий пример комплементарной (контрастной) схемы. Выстраивается на цветах диаметрально противоположных друг другу на круге. Вызывает сильное воздействие на зрителя и отлично подходит для интерьеров.

Закат

Классическая триада. Образуется при помощи равностороннего треугольника, мысленного помещенного в центр круга. Концы его углов касаются трех цветов, которые отлично балансируют картинку. Вращайте треугольник по кругу
и получайте различные триадные оттенки. В конкретном примере использованы красный, фиолетовый и оранжевый. Подборка подходит для оформления рекламных щитов, флаеров, плакатов и художественных снимков.

Нежность

Нейтрально-спокойные тона дарят ощущение умиротворенности. Используйте аналогичную цветовую схему в дизайне спальни или для стильной постобработки снимков для инстаграма.

Пряность

Объединение теплых коричневых и бежевых оттенков, преподнесенных в разных контекстах, могут знаменовать собой сладость вкуса, умеренность, фундаментальность. На примере ниже вы можете видеть, что фон изображения обработан в единой гамме, но все присутствующие на фото оттенки коричневого при этом имеет сильную тональную разбежность. Такой подход не дает сливаться объектам в сплошное цветовое пятно, а позволяет расставить акценты.

Холодные сочетания

Море

Монохромная схема. Представляет собой два-три соседних оттенка на круге. Здесь воплощена при помощи холодных тонов, вызывающих ощущение отстраненности и свежести.

Арктика

По законам колористики холодные оттенки отдаляют объект. Если они при этом светлые, то в зрителе пробуждаются ассоциации со свежим морозным утром и чистым горным воздухом. Сочетание серо-голубых цветов можно с успехом использовать в летних рекламных кампаниях, когда освежает один только взгляд на плакат.

Роза

Еще один пример классической триады. На этот раз – в строгих холодных тонах.

Свежие сочетания

Горы

Здесь применяется родственная схема. Голубой и зеленый в различных оттеночных вариациях отлично гармонируют между собой. Серый хорошо приглушает цвета, придавая картинке сдержанность. В то же время яркие цветовые пятна — пронзительная лазурь небес и яркая зелень травы — создают необходимые акценты.

Свежесть

Очередная монохромная схема, построенная на использовании холодного зеленого цвета. Подойдет для тех, кто
не боится оттолкнуть аудиторию. Используйте программу для редактирования фото, чтобы привести зелень к чистому цвету, исключающему всякий намек на желтизну и убрать лишнюю насыщенность.

Цитрусовый микс

Цитрусовые оттенки бодрят и настраивают на оптимистичный лад. Сочетание цвета, представленное в цветах на фото зеленым и оранжевым можно рекомендовать для оформления детских и игровых комнат, кухонь и использовать
для оформления буклетов для отдыхающих в пансионатах, санаториях и проч.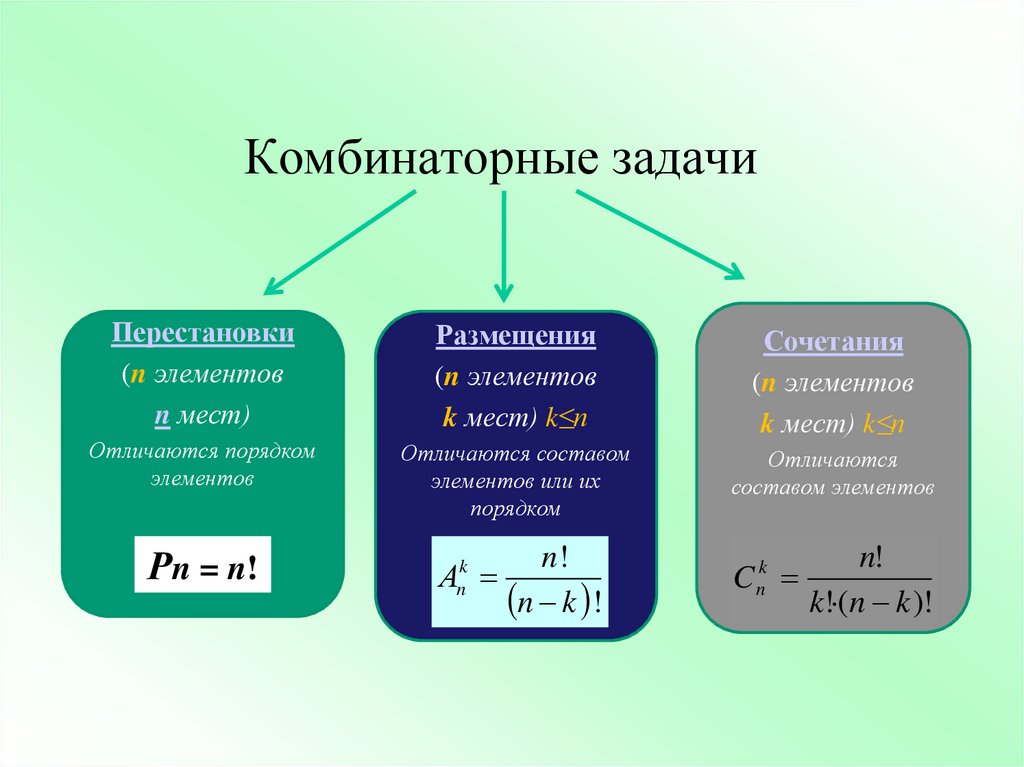

Темные схемы

Медная гора

Циановый хорошо гармонирует с охристым глиняным цветом гор. Обработка, основанная на контрастной схеме,
где света красятся в холодные голубые оттенки, а тени в теплые оранжевые, давно завоевала популярность, и активно используется в кинематографе и цифровой фотографии.

Аппетитный суп

Часто для обработки фуд-фото применяют темные цвета, контрастирующие с главным объектом съемки, который
как раз высветляют. Это помогает привлечь взгляд зрителя к определенной области.

Яркие схемы

Цветочный луг

На картинке видим сочетание из двух комплементарных цветов: желтый – синий и зеленый – красный (розовый). Комбинация четырех оттенков позволяет внести разнообразие в иллюстрацию и придать ему красочность.

Тропический рай

Комплементарная расщепленная схема: красный разбит на малиновый и светло-розовый и противостоит зеленому. Оранжевого оттенка на снимке настолько мало, что его в схеме не учитывают. Смешение большого количества цветов оживляет картинку. Она смотрится чуть менее контрастно, нежели стандартная двухцветная схема, а также более реалистично и интересно. В интернете есть программы-генераторы цветовых сочетаний, но они работают некорректно. Зачастую выдают результаты, приближенные к реальным, но лучше научиться «читать» такие схемы самостоятельно.

Мягкие сочетания

Бирюза

Нежные чуть приглушенные оттенки розового и бирюзового как нельзя лучше подойдут для оформления товаров, предназначенных для малышей или домашнего хозяйства.

Зефир

Здесь палитра сочетания цветов ограничена соединением мягких пастельных тонов. Это напоминает о чем-то легком воздушном, что будет уместно смотреться в рекламе кондитерских изделий, косметики, кафе, детских товаров.

Букет невесты

Очередной пример схемы с расщеплением. Контрастный желтый противостоит красному в его наиболее блеклом оттенке – розовом. Схема приглушена по тональности и разбавлена белым оттенком. В целом изображение смотрится очень гармонично и нежно. Отлично впишется в медицинские рекламные кампании и рекламу здорового питания.

Вывод

Для того, чтобы осуществить подбор нужной цветовой комбинации вы всегда можете воспользоваться изображением круга Иттена, а для расширения знаний в этой области ознакомиться с книгой «Искусство цвета». Конечно, сначала нужно скачать фоторедактор (например, ФотоМАСТЕР), и неустанно оттачивать мастерство. Не надейтесь на «Кулер»
в Фотошопе или подобные инструменты, они выдают несовершенные результаты, и никогда не заменят вам собственных теоретических познаний, подкрепленных практикой.

Подпишитесь:

Мы в

Простые перестановки и комбинации — BetterExplained

Я всегда путал «перестановку» и «комбинацию» — какая из них какая?

Вот простой способ запомнить: перестановка звучит сложно , не так ли? И это. В перестановках важна каждая мелочь. Алиса, Боб и Чарли отличаются от Чарли, Боба и Алисы (вставьте сюда имена ваших друзей).

Комбинации, с другой стороны, довольно просты. Детали не имеют значения. Алиса, Боб и Чарли такие же, как Чарли, Боб и Алиса.

Перестановки для списков (порядок имеет значение), а комбинации для групп (порядок не имеет значения).

Вы знаете, «кодовый замок» действительно должен называться «замком перестановки». Порядок, в котором вы ставите числа, имеет значение.

Настоящий «кодовый замок» будет принимать как 10-17-23, так и 23-17-10 как правильные.

Перестановки: Волосатые детали

Начнем с перестановок, или всех возможных способов что-то сделать. Мы используем модный термин «перестановка», поэтому мы позаботимся о каждой детали, включая порядок каждого элемента. Допустим, у нас есть 8 человек:

 1: Алиса
2: Боб
3: Чарли
4: Дэвид
5: Ева
6: Фрэнк
7: Джордж
8: Горацио

Сколькими способами мы можем присудить 1-е, 2-е и 3-е место среди восьми участников? (Золото / Серебро / Бронза)

Мы собираемся использовать перестановки, поскольку порядок, в котором мы раздаем эти медали, имеет значение. Вот как это выглядит:

Золотая медаль: 8 вариантов: A B C D E F G H (умно, как я сопоставил имена с буквами, а?). Допустим, А выигрывает золото.
Серебряная медаль: 7 вариантов: B C D E F G H. Допустим, B выиграет серебро.
Бронзовая медаль: 6 вариантов: C D E F G H. Допустим… C выигрывает бронзу.

Мы выбрали определенных людей, чтобы выиграть, но детали не имеют значения: у нас было сначала 8 вариантов, затем 7, затем 6. Общее количество вариантов было 8 $ * 7 * 6 = 336 $.

Давайте посмотрим на детали. Пришлось заказывать 3 человека из 8. Для этого мы начинали со всех вариантов (8) потом забирали их по одному (7, потом 6) пока не кончились медали.

Мы знаем, что факториал:

К сожалению, это слишком много! Мы хотим только $8 * 7 * 6$. Как мы можем «остановить» факториал на 5?

Вот где перестановки становятся крутыми: обратите внимание, как мы хотим избавиться от $5 * 4 * 3 * 2 * 1$. Какое другое название для этого? 5 факториал!

Итак, если мы сделаем 8!/5! получаем:

А почему мы использовали цифру 5? Потому что она осталась после того, как мы взяли 3 медали из 8. Таким образом, лучше написать это так:

, где 8!/(8-3)! — это просто причудливый способ сказать: «Используйте первые 3 числа из 8!». Если у нас есть 9Всего 0005 n предметов и вы хотите выбрать k в определенном порядке, мы получаем:

И это причудливая формула перестановки: У вас есть n предметов и вы хотите найти количество способов k предметов можно заказать:

Комбинации, Хо!

Комбинации легки. Порядок не имеет значения. Вы можете смешать это, и это будет выглядеть так же. Допустим, я скряга и не могу позволить себе отдельные золотые, серебряные и бронзовые медали. На самом деле, я могу позволить себе только пустые жестяные банки.

Сколькими способами я могу раздать 3 консервные банки 8 людям?

Ну, в данном случае порядок, в котором мы выбираем людей, не имеет значения. Если я даю банку Алисе, Бобу, а затем Чарли, это то же самое, что дать Чарли, Алисе, а затем Бобу. В любом случае, они одинаково разочарованы.

Это поднимает интересный вопрос — у нас здесь есть некоторые излишества. Элис Боб Чарли = Чарли Боб Элис. На минутку давайте просто выясним, сколькими способами мы можем переставить 3 человек.

Итак, у нас есть 3 варианта для первого человека, 2 для второго и только 1 для последнего. Итак, у нас есть $3 * 2 * 1 $ способов переставить 3 человек.

Минуточку… это немного похоже на перестановку! Ты обманул меня!

Действительно. Если у вас есть N человек, и вы хотите знать, сколько существует договоренностей для всех из них, это просто N факториал или N!

Итак, если у нас есть 3 жестяных банки для раздачи, их будет 3! или 6 вариантов для каждого выбора, который мы выбираем. Если мы хотим выяснить, сколько комбинаций у нас есть, мы просто создаем все перестановки и делим на все избыточности . В нашем случае мы получаем 336 перестановок (сверху), делим на 6 избыточностей для каждой перестановки и получаем 336/6 = 56,9.0003

Общая формула:

, что означает «Найдите все способы выбрать k людей из n и разделите на k! варианты». Записав это, мы получим нашу формулу комбинации , или количество способов объединить k элементов из набора n:

Иногда C(n,k) записывается как: биномиальный коэффициент.

Несколько примеров

Вот несколько примеров комбинаций (порядок не имеет значения) из перестановок (порядок имеет значение).

Комбинация: Выбор команды из 3 человек из группы 10. $C(10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.
Перестановка: выбор президента, вице-президента и мальчика-водопровода из группы из 10 человек. $P(10,3) = 10!/7! = 10 * 9 * 8 = 720$.
Комбинация: выбор 3 десертов из меню из 10. C(10,3) = 120.
Перестановка: Перечислите 3 ваших любимых десерта по порядку из меню из 10. P(10,3) = 720.

Не запоминайте формулы, поймите, почему они работают. Комбинации звучат проще, чем перестановки, и это так. У вас меньше комбинаций, чем перестановок.

Другие сообщения из этой серии

Простые перестановки и комбинации
Навигация по сетке с использованием комбинаций и перестановок
Как понимать комбинации с помощью умножения
Почему мы умножаем комбинации?

Комбинации — определение, формула, примеры, часто задаваемые вопросы

Комбинации также называются выборками. Комбинации соответствуют выбору вещей из заданного набора вещей. Здесь мы не собираемся устраивать вещи. Мы намерены выбрать их. Обозначим количество уникальных 9п{С_г}\).

Комбинации отличаются от аранжировок или перестановок. Давайте узнаем больше о том, как рассчитать комбинации, формулы комбинаций, различия между перестановками и комбинациями, с помощью примеров, часто задаваемых вопросов.

1.	Что такое комбинации?
2.	Что такое формула комбинаций?
3.	Комбинации как выборки
4.	Как применять формулы комбинаций?
5.	Связь между перестановками и комбинациями
6.	Примеры комбинаций
7.	Часто задаваемые вопросы о комбинациях

Что такое комбинации?

Комбинации — это выборки, сделанные путем взятия некоторых или всех объектов, независимо от их расположения. n C_r\).

Эта формула для нахождения количества комбинаций с использованием r объектов из n объектов также называется формулой ncr.

Что такое формула комбинаций?

Формула комбинаций используется для простого нахождения количества возможных различных групп по r объектов в каждой, которые могут быть сформированы из доступных n различных объектов. Формула комбинаций представляет собой факториал n, деленный на произведение факториала r и факториала разности n и r соответственно. 9nC_r = \dfrac{n!}{r!.(n — r)!}\)

Формула комбинаций также называется формулой ncr. Чтобы использовать формулу комбинаций, нам нужно знать значение факториала, и у нас есть n! = 1 × 2 × 3 × …. (n — 1) × n.

Комбинации как выбор

Предположим, у нас есть набор из 6 букв {A,B,C,D,E,F}. Сколькими способами мы можем выбрать группу из 3 букв из этого набора? Предположим, мы находим количество возможных комбинаций из 3 букв из этих 6 букв. Это число будет ⁶ П$_3$. Рассмотрим перестановки, содержащие буквы A, B и C. Их 3! = 6 путей, а именно ABC, ACB, BAC, BCA, CAB и CBA.

Теперь нам нужно количество комбинаций, а не количество аранжировок. Другими словами, 6 перестановок, перечисленных выше, будут соответствовать одной комбинации. Иными словами, порядок вещей не важен; теперь в нашем выборе имеет значение только группа/комбинация. Это означает, что общее количество комбинаций из 3 букв из доступного нам набора из 6 букв будет равно 9.n{P_r}}{r} = \dfrac{n!}{r!(n — r)!}\)

Связь между перестановками и комбинациями

Формулы и концепции перестановок и комбинаций имеют много общего. Предположим, что у вас есть n различных объектов. Вы должны определить количество уникальных r -выборов (выборов, содержащих r объектов), которые можно сделать из этой группы из n объектов. Представьте себе группу из 90 155 n 90 156 человек — вам нужно найти количество уникальных подгрупп размера 9. nC_r = \dfrac{n!}{r!.(n — r)!}\). 9nC_r = \dfrac{n!}{r! (н-р)!}\). Для заданных r вещей из n вещей количество перестановок больше, чем количество комбинаций.

Каковы примеры комбинаций?

Примеры комбинаций включают в себя группы, образованные из разнородных объектов. Формирование комитета, спортивная команда, набор различных стационарных объектов, команда людей – вот некоторые из примеров комбинаций.

Комбинации — примеры и практические задачи

Комбинации используются для подсчета количества различных способов, которыми определенные группы могут быть выбраны из набора, если порядок объектов не имеет значения. Это отличается от перестановок, где порядок объектов имеет значение.

Здесь мы рассмотрим краткое описание комбинаций вместе с их формулой и используемой терминологией. Кроме того, мы увидим примеры с ответами, чтобы узнать о применении формулы комбинации.

АЛГЕБРА

Актуально для …

Изучение комбинаций с решенными примерами.

См. примеры

Содержание

АЛГЕБРА

Актуально для …

Изучение комбинаций с решенными примерами.

См. примеры

Сводка комбинаций

Комбинации — это выбор объектов в наборе, в котором порядок выбора не имеет значения. В комбинациях мы можем выбирать объекты в любом порядке. Например, если у нас есть ab и ba , эти выборки считаются равными в комбинациях.

Формула для определения числа возможных организаций путем выбора нескольких объектов из набора без повторений выражается следующим образом:

$латекс _{n}{{C}_{k}}=\frac{{n!}}{{\left({nk} \right)!k!}}$

где:

n это общее количество элементов в наборе
k это количество выбранных объектов
! является символом факториала

Напомним, что факториал (обозначается как «!») — это произведение всех положительных целых чисел, меньших или равных числу, предшествующему факториалу. Например, $latex 3!=1 \times 2 \times 3 = 6$.

Комбинации – Примеры с ответами

На следующих примерах вы можете попрактиковаться в применении формулы комбинации. Каждое упражнение имеет свое решение для анализа аргументации каждого ответа.

ПРИМЕР 1

Найдите результат комбинации $latex _{8}C_{6}$.

Решение

Используем формулу комбинаций $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!} }$ и подставить $latex n=8$ и $latex k=6$:

$latex _{8}{{C}_{6}}=\frac{{8!}}{{\left( {8-6} \right)!6!}}$

$latex = \frac{{8!}}{{\left( {2} \right)!6!}}$

Теперь мы понимаем, что можем записать 8! как $latex 8 \times 7 \times 6!$ и мы исключаем 6! как в числителе, так и в знаменателе:

$latex \frac{{8!}}{{\left( {2} \right)!6!}}=\frac{{8\times 7}}{2 }$

$latex =4\times 7=28$

ПРИМЕР 2

Найдите результат комбинации $latex _{9}C_{4}$.

Решение

Подставляем $latex n=9$ и $latex k=4$ в формулу $latex _{n}{{C}_{k}}=\frac{{n!}}{{\ left( {n-k} \right)!k!}}$:

$latex _{9}{{C}_{4}}=\frac{{9!}}{{\left( {9-4 } \right)!4!}}$

$latex =\frac{{9!}}{{\left( {5} \right)!4!}}$

Теперь мы понимаем, что можем писать до 9! как $латекс 9\раз 8\раз 7\раз 6\раз 5!$ и мы исключаем 5! как в числителе, так и в знаменателе:

$latex \frac{{9!}}{{\left( {5} \right)!4!}}=\frac{{9\times 8\times 7\times 6}}{4!}$

Переписываем 4! как $latex 4\times 3\times 2\times 1$ и упростить:

$latex \frac{{9\times 8\times 7\times 6}}{4\times 3\times 2\times 1}= 126$

Начните прямо сейчас: изучите наши дополнительные ресурсы по математике

ПРИМЕР 3

Найдите комбинацию $latex _{100}C_{100}$.

Решение

Подставляем $latex n=100$ и $latex k=100$ в формулу $latex _{n}{{C}_{k}}=\frac{{n!}}{{\ влево( {n-k} \right)!k!}}$:

$latex _{100}{{C}_{100}}=\frac{{100!}}{{\left( {100-100} \right)!100!}}$

$latex = \frac{{100!}}{{\left( {1} \right)!100!}}$

Мы можем легко исключить 100! знаменатель и числитель:

$latex \frac{{100!}}{{\left( {1} \right)!100!}}=1$

Этот результат имеет смысл, поскольку существует только один возможный способ выберите 100 объектов из набора 100 объектов, если порядок не имеет значения.

ПРИМЕР 4

Сколькими способами можно выбрать команду из 3 человек из 10?

Решение

В этом случае мы выбираем 3 человек, поэтому $латекс k=3$. Вся группа состоит из $латекса n=10$. Используя эти данные в формуле $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!}}$, мы имеем :

$латекс _{10}{{C}_{3}}=\frac{{10!}}{{\left( {10-3} \right)!3!}}$

$латекс =\frac{{10!}}{{\left( {7} \right)!3!}}$

Мы можем расширить 10! пока не наберешь 7! и упростим это:

$latex \frac{10!}{(3)!3!}=\frac{10\times 9 \times 8 \times 7!}{(7)!3!}$

$latex =\frac{{10\times 9 \times 8}}{{3!}}$

$latex =\frac{{10\times 9 \times 8}}{{6}}$

$latex =120$

ПРИМЕР 5

Предположим, нам нужно выбрать 5 новых сотрудников из списка из 10 претендентов. Сколькими способами это можно сделать?

Решение

В этом случае у нас есть $latex n=10$ и $latex k=5$, поэтому имеем:

$latex _{10}{{C}_{5}}=\frac {{10!}}{{\left( {10-5} \right)!5!}}$

$latex =\frac{{10!}}{{\left( {5} \right)! 5!}}$

Мы можем переписать 10! пока не получим 5! и упростить:

$latex \frac{{10!}}{{\left( {5} \right)!5!}}=\frac{{10 \times 9\times 8 \times 7 \times 6 \ раз 5!}}{{\left( {5} \right)!5!}}$

$latex =\frac{{10 \times 9\times 8 \times 7 \times 6}}{{5! }}$

$latex =\frac{10 \times 9\times 8 \times 7 \times 6}{5 \times 4\times 3 \times 2 \times 1}$

$latex =252$

ПРИМЕР 6

В автосалоне есть 3 автомобиля одной модели, которые необходимо перевезти в другой автосалон. Если всего имеется 25 автомобилей этой модели, сколько вариантов транспорта доступно?

Решение

Признаем, что у нас есть $latex n=25$ y $latex k=3$ и подставляем эти значения в формулу $latex _{n}{{C}_{k}}=\frac{ {n!}}{{\left( {nk} \right)!k!}}$:

$latex _{25}{{C}_{3}}=\frac{{25!}}{ {\left( {25-3} \right)!3!}}$

$latex =\frac{{25!}}{{\left( {22} \right)!3!}}$

Перепишем факториал 25! пока не дойдем до 22!:

$latex \frac{{25!}}{{\left( {22} \right)!3!}}=\frac{{25 \times 24 \times 23 \times 22 !}}{{\left( {22} \right)!3!}}$

Теперь упрощаем до 22! в числителе и знаменателе:

$latex \frac{{25 \times 24 \times 23 \times 22!}}{{\left( {22} \right)!3!}}=\frac{{25 \ умножить на 24 \раз 23}}{{3!}}$

$latex =25 \times 4 \times 23=2300$

ПРИМЕР 7

Предположим, у нас есть офис из 5 женщин и 6 мужчин, и мы необходимо выбрать комиссию из 4 человек. Сколькими способами можно выбрать 2 мужчин и 2 женщин?

Решение

В этом случае нам нужно найти две разные комбинации, а затем перемножить их. Поэтому мы хотим вычислить $latex (_{5}{{C}_{2}})(_{6}{{C}_{2}})$. Мы можем посчитать эти комбинации по отдельности:

$latex _{5}{{C}_{2}}=\frac{{5!}}{{\left( {5-2} \right)!2!}}$

$latex = \frac{{5!}}{{\left( {3} \right)!2!}}$

$latex =\frac{{5\times 4\times 3!}}{{\left( { 3} \right)!2!}}$

$latex =\frac{{5\times 4}}{{2!}}=10$

$latex _{6}{{C}_{2 }}=\frac{{6!}}{{\left( {6-2} \right)!2!}}$

$latex =\frac{{6!}}{{\left( {4 } \right)!2!}}$

$latex =\frac{{6\times 5\times 4!}}{{\left( {4} \right)!2!}}$

$latex =\frac{{6\times 5}}{{2!}}=15$

Следовательно, у нас есть $латекс (_{5}{{C}_{2}})(_{6}{{C}_{2}})=10\times 15=150$.

→ Калькулятор комбинаций (nCr)

Комбинации – практические задачи

Примените свои знания о комбинациях на практике, решая следующие задачи. Решите комбинации и выберите ответ. Пожалуйста, проверьте его, чтобы убедиться, что вы выбрали правильный.

Найдите комбинацию $latex _{9}C_{5}$.

Выберите ответ

126

144

Найдите комбинации $latex _{11}C_{9}$.

Выберите ответ

Сколько комбинаций получится, если мы возьмем 2 предмета из набора из 7?

Выберите ответ

122

Мы хотим выбрать команду из 6 человек из 9. Сколько существует способов добиться этого?

Выберите ответ

На собрании 10 человек. Если все пожмут друг другу руки, сколько рукопожатий возможно?

Выберите ответ

См.

также

Хотите узнать больше о факториалах, перестановках и комбинациях? Взгляните на эти страницы:

Калькулятор комбинаций (nCr)
Примеры факториалов
Примеры перестановок

Изучайте математику с помощью наших дополнительных ресурсов по различным темам

ПОДРОБНЕЕ

Перестановки и комбинации: различия и примеры

В математике и статистике перестановки и комбинации — это два разных способа взять набор элементов или вариантов и создать подмножества. Например, если у вас десять человек, сколько подмножеств из трех можно составить? Хотя перестановка и комбинация кажутся синонимами в повседневном языке, математически они имеют разные определения.

Перестановки : Порядок результатов имеет значение.
Комбинации : Порядок не имеет значения.

Давайте разберем эту разницу между перестановкой и комбинацией более подробно. И тогда вы узнаете, как рассчитать общее количество каждого.

В некоторых сценариях порядок результатов имеет значение. Например, если у вас есть замок, где вам нужно ввести четыре цифры, порядок имеет значение. Если правильные числа 8 3 6 2, вы не можете ввести те же числа в любом другом порядке (например, 6 8 2 3) и ожидать, что замок откроется! Следовательно, это перестановка.

На самом деле мы должны называть этот тип блокировки блокировкой перестановки!

И наоборот, порядок опций не имеет значения для комбинаций. Представьте, что вы готовите пиццу с пепперони (P), ветчиной (H) и грибами (M). Неважно, готовите ли вы пиццу PHM, HMP или MPH. Это все та же пицца! В данном случае порядок не имеет значения, так что это комбинация.

В некоторых случаях определение того, является ли что-либо перестановкой или комбинацией, зависит от условий, определяемых решаемой вами задачей. Например, выбор пяти человек в группу, где у всех одинаковая роль, является комбинацией, поскольку порядок их выбора не имеет значения.

Однако, если вы выбираете пять человек и их роль зависит от того, когда вы их выбираете, это перестановка, потому что порядок имеет значение. Например, первый человек может быть ведущим, второй — вести заметки и так далее.

Примеры перестановок и комбинаций

Перестановки	Комбинация
Последовательность цифр для замка.	Числа для выигрыша в лотерею.
Подбор людей в команду по должности.	Выбор детей в члены класса.
Выбор первого, второго и третьего мест.	Выбираем трех финалистов.

Формулы подсчета перестановок и комбинаций

Часто, когда вы работаете с перестановками и комбинациями, вам нужно подсчитать количество возможных вариантов. Теперь, когда вы понимаете разницу между концепциями, давайте посмотрим, как вы считаете количество перестановок и комбинаций. Когда у вас есть как минимум две перестановки, у вас будет больше возможностей, чем соответствующее количество комбинаций.

Почему так? Пример с пиццей показывает, что PHM, HMP и MHP представляют собой одну и ту же комбинацию. Однако, если мы используем эти три буквы в качестве пароля, это три разные перестановки.

Пример перестановки

Порядок перестановок имеет значение. Предположим, нам нужно знать количество возможностей для четырехзначного замка. Есть 10 возможных значений, и мы выбираем 4. Статистики формулируют этот сценарий как «10 выбирают 4» и обозначают его как ₁₀ P ₄ , где P означает, что мы работаем с перестановками. Сколько существует перестановок для этого сценария?

Это зависит от того, разрешаем ли мы повторяющиеся значения или нет. Может ли последовательность блокировки использовать 1 1 2 3? Или вы можете использовать каждую цифру только один раз?

Если последовательность может повторять значения, то каждая из четырех цифр имеет десять вариантов (0–9). Следовательно, четырехзначный замок имеет 10 * 10 * 10 * 10 = 10 ⁴ = 10 000 перестановок. Однако, если значения не могут повторяться, то существует 10 * 9* 8 * 7 = 5040. Уменьшающиеся значения во втором расчете представляют меньше вариантов, доступных для каждой последующей цифры, когда вы не можете повторно использовать предыдущие значения.

Пример комбинации

Теперь предположим, что у нас есть 10 начинок для пиццы, и мы выбираем 4 из них. Мы обозначаем это как ₁₀ C ₄ .

Эта схема с 10 вариантами и выбором 4 аналогична примеру с перестановкой, за исключением того, что теперь мы работаем в условиях, когда порядок не имеет значения, что помогает проиллюстрировать разницу между перестановкой и комбинацией. Сколько существует комбинаций?

Для расчета количества комбинаций с повторениями используйте следующую формулу:

Где:

n = количество вариантов.
р = размер каждой комбинации.

Восклицательный знак (!) обозначает факториал. В общем, н! равно произведению всех чисел до n. Например, 3! = 3 * 2 * 1 = 6. Исключение 0! = 1, что упрощает уравнения.

В нашем примере n = 10 и r = 4, потому что доступно 10 начинок, и мы выберем 4. Давайте введем эти значения в уравнение, позволяющее повторить:

Существует 715 комбинаций, в которых можно повторять ингредиенты. Это означает, что мы можем получить двойную, тройную или даже четверную порцию пепперони!

Если нельзя повторять значения, формула следующая:

Ввод значений в уравнение без повторения:

Существует 210 комбинаций, когда нельзя повторять ингредиенты. Мы можем получить ингредиент только один раз — никаких двойных пепперони!

Как и ожидалось, число возможностей для ₁₀ C ₄ намного ниже, чем для примера ₁₀ P ₄.

Использование перестановок и комбинаций для решения вероятностных задач

Этот обзор лишь поверхностно описывает использование перестановок и комбинаций. Для получения более подробной информации о каждом из них, а также рабочих примеров для решения вероятностных задач, пожалуйста, прочитайте мои отдельные статьи о:

Использование перестановок для решения вероятностных задач
Использование комбинаций для решения вероятностных задач

Задачи на перестановки и комбинации

Перестановки и комбинации используются для решения задач.

Пример 1. Сколько трехзначных чисел можно составить, используя цифры 1, 2 и 3 без повторений? Метод
(1), перечисляющий все возможные числа с использованием древовидной диаграммы.

Мы можем составить 6 чисел, используя 3 цифры и не повторяя цифры.
метод (2) подсчета:
ПОСМОТРИТЕ НА ДРЕВЕСНУЮ СХЕМУ ВЫШЕ.
У нас есть 3 варианта для первой цифры, 2 варианта для второй цифры и 1 вариант для третьей цифры.
Используя принцип счета, мы можем сказать:
Общее количество трехзначных чисел определяется как
3 2 1 = 6
Произведение 3 2 1 = 3 имеет специальное обозначение! и читается 3 факториал.
Вообще н! читается как факториал и определяется как
н! = n(n — 1)(n — 2)…21
Мы также определяем 0! = 1.

Пример 2. Сколько разных слов можно составить из букв A, B, E и L?
Решение: у нас есть 4 варианта для первой буквы, 3 варианта для второй буквы, 2 варианта для третьей буквы и 1 вариант для четвертой буквы. Следовательно, количество слов равно 4 3 2 1 = 4! = 24
Пример 3. Сколько двузначных чисел можно составить, используя цифры 1, 2, 3 и 4, не повторяя цифры?
На этот раз мы хотим использовать 2 цифры, чтобы получить 2-значные числа.
Для первой цифры у нас есть 4 варианта, а для второй цифры у нас есть 3 варианта (4 — 1 уже используется). Используя принцип подсчета, количество двузначных чисел, которые мы можем составить, используя 4 цифры, определяется выражением 4 3 = 12
Вышеупомянутая проблема состоит в том, что упорядочивает 2 цифры из 4 в определенном порядке.

Это также называется перестановкой.
Самая важная идея в перестановках состоит в том, что порядок важен . Когда вы используете цифры 3 и 4 для составления числа, числа 34 и 43 различны, поэтому важен порядок цифр 3 и 4.
Обычно перестановка r (2 цифры в приведенном выше примере) элементов из набора из n (4 цифры в приведенном выше примере) элементов записывается как _n P _r и формула имеет вид
_n P _r = n! / (н — р)!
Пример 4: Расчет
₄ П ₂
₆ П ₅
₄ П ₄
Решение:
₄ P ₂ = 4! / (4 — 2)! = 24/2 = 12
₆ П ₅ = 6! / (6 — 5)! = 654321 / 1! = 720
₄ P ₄ = 4! / (4 — 4)! = 4! / 0! = 4! = 4321 = 24 (Теперь мы понимаем необходимость определения 0! = 1)
Пример 5: Сколько трехбуквенных слов мы можем составить из букв в слове ЛЮБОВЬ?
Решение: В слове «любовь» 4 буквы, и составление слов из 3 букв аналогично расположению этих 3 букв, и порядок важен, поскольку LOV и VOL — разные слова из-за порядка одинаковых букв L, O и V.

Следовательно это проблема перестановки. Количество слов определяется
₄ P ₃ = 4! / (4 — 3)! = 24

Комбинации

Пример 6: Сколько прямых можно провести, используя 3 не лежащие на одной прямой (не лежащие на одной прямой) точки A, B и C на плоскости?

Решение:
Чтобы провести линию, нужно две точки. Порядок не важен. Линия АВ такая же, как и линия ВА. Задача состоит в том, чтобы выбрать 2 точки из 3, чтобы провести разные линии. Если мы поступим так же, как и с перестановками, мы получим следующие пары точек для рисования линий.
АБ, АС
BA, Британская Колумбия
КА, КБ
Возникла проблема: линия AB совпадает с линией BA, одинаково для линий AC и CA, BC и CB.
Линии: AB, BC и AC; всего 3 строчки.
На самом деле мы можем провести 3 линии, а не 6, потому что в этой задаче порядок точек A, B и C не важен.
Это задача на комбинирование: объединение 2 предметов из 3 и записывается следующим образом:

_n C _r = n! / [(н — р)! р! ]
Количество комбинаций равно количеству перестановок, деленному на r! to устраняет те, которые учитывались более одного раза, потому что порядок не важен.

Пример 7: Расчет
₃ С ₂
₅ С ₅
Решение:
₃ С ₂ = 3! / [ (3 — 2)!2! ] = 6 / [1 2] = 3 (задача точек и прямых решена выше в примере 6)
₅ С ₅ = 5! / [(5 — 5)!5! ] = 5! / [0!5!] = 5! / [1 5!] = 1 (есть только один способ выбрать (без порядка) 5 элементов из 5 элементов и выбрать их все один раз!)
Пример 8: Нам нужно сформировать команду из 5 человек в классе из 12 учеников.

Сколько различных команд можно сформировать?
Решение:
Нет ничего, что указывало бы на то, что порядок, в котором выбираются члены команды, важен, и поэтому это проблема комбинирования. Следовательно, количество команд равно
₁₂ С ₅ = 12! / [(12 — 5)!5! ] = 792

Задачи

Сколько четырехзначных чисел можно составить, используя цифры 3, 6, 7 и 8 без повторений?
Сколько трехзначных чисел можно составить, используя цифры 2, 3, 4, 5 и 6 без повторений?
Сколько слов из 6 букв можно составить из букв слова СВОБОДА без повторений?
Сколькими способами можно расставить на полке 5 разных книг?
Сколькими способами можно выбрать комиссию из 3 студентов из 10?
Сколько треугольников можно составить, используя 6 не лежащих на одной плоскости точек?
Из группы 10 юношей и 12 девушек сформировать комитет в составе 3 юношей и 4 девушек. Сколько различных комитетов можно сформировать из группы?
В определенной стране номерной знак автомобиля состоит из 4 цифр из цифр 1, 2, 3, 4, 5, 6, 7, 8 и 9, за которыми следуют 3 буквы алфавита. Сколько номерных знаков можно составить, если ни цифры, ни буквы не повторяются?

решения вышеуказанных проблем

4! = 24
₅ Р ₃ = 60
₇ Р ₆ = 5040
5! = 120
₁₀ С ₃ = 120
₆ С ₃ = 20
₁₀ С ₃ ₁₂ с ₄ = 59 400
₉ P ₄ ₂₆ P ₃ = 47 174 400

Еще Ссылки и ссылки

элементарная статистика и вероятности. Калькулятор комбинаций. Подсчитайте количество комбинаций из n элементов, взятых за r в момент времени.
Калькулятор перестановок. Подсчитайте количество перестановок n элементов, взятых за r в момент времени.

сообщите об этом объявлении

задач на перестановки и комбинации | GMAT GRE Учебник по математике

В этой статье вы узнаете о задачах на перестановку и комбинацию: определение, формулы, решенные примеры и тест с практическими вопросами.

Перестановки

Определение

Перестановки — это различные способы организации набора элементов.

Например:

Различные способы группировки алфавитов A, B и C, взятые все одновременно, это ABC, ACB, BCA, CBA, CAB, BAC.

Обратите внимание, что ABC и CBA не совпадают, так как порядок расположения отличается. То же правило применяется при решении любой задачи в Permutations.

Количество способов, которыми можно упорядочить n вещей, взятых одновременно, ⁿ P _n = n!, называется «n факториалом».

Формула факториала определяется как произведение всех чисел от n до 1.

Например, факториал 5, 5! = 5*4*3*2*1 = 120.

Таким образом, количество способов, которыми можно расположить 3 буквы за все время, равно 3! = 3*2*1 = 6 способов.

Количество перестановок n вещей, взятых по r за раз, обозначается:

ⁿ P _r = n! / (н-р)!

Например:

Три буквы, взятые по две за раз, можно расставить по-разному: 3!/(3-2)! = 3!/1! = 6 способов.

Важные формулы перестановки

1! = 1

0! = 1

Давайте рассмотрим несколько примеров:

Задача 1: Найдите количество слов со значением или без значения, которые можно составить из букв слова «СТУЛ».

Решение :

«КРЕСЛО» состоит из 5 букв.

Следовательно, количество слов, которые можно составить из этих 5 букв = 5! = 5*4*3*2*1 = 120.

Задача 2: Найдите количество слов со значением или без значения, которые можно составить из букв слова «ИНДИЯ».

Решение :

Слово «ИНДИЯ» состоит из 5 букв, а «И» встречается дважды.

Если буква встречается в слове более одного раза, мы делим факториал числа всех букв в слове на количество вхождений каждой буквы.

Следовательно, количество слов, образованных словом «ИНДИЯ» = 5!/2! = 60.

Задача 3: Найдите количество слов со смыслом или без, которые можно составить из букв слова «ПЛАВАНИЕ?»

Решение :

Слово «ПЛАВАНИЕ» состоит из 8 букв. Из которых I встречается дважды, а M встречается дважды.

Следовательно, количество слов, образованных этим словом = 8! / (2!*2!) = 10080.

Задача 4: Сколько различных слов можно составить из букв слова «СУПЕР» так, чтобы гласные всегда совпадали?

Решение :

Слово «СУПЕР» состоит из 5 букв.

Для того, чтобы найти количество перестановок, которые могут быть образованы, когда две гласные U и E встречаются вместе.

В этих случаях мы группируем буквы, которые должны собраться вместе, и рассматриваем эту группу как одну букву.

Итак, буквы S,P,R, (UE). Теперь количество слов равно 4.

Следовательно, количество способов, которыми можно расположить 4 буквы, равно 4!

В U и E количество способов, которыми можно расположить U и E, равно 2!

Следовательно, общее количество способов, которыми буквы «SUPER» могут быть расположены так, чтобы гласные всегда были вместе, равно 4! * 2! = 48 способов.

Задача 5: Найдите количество различных слов, которые можно составить из букв слова «МАСЛО» так, чтобы гласные всегда были вместе.

Решение :

Слово «МАСЛО» состоит из 6 букв.

Буквы U и E всегда должны совпадать. Итак, буквы Б, Т, Т, Р, (УЭ).

Количество способов, которыми можно расположить буквы выше = 5!/2! = 60 (поскольку буква «Т» повторяется дважды).

Количество способов расположения U и E = 2! = 2 способа

Следовательно, общее количество возможных перестановок = 60*2 = 120 способов.

Задача 6: Найдите количество перестановок букв в слове REMAINS, чтобы гласные всегда стояли на нечетных местах.

Решение :

Слово «ОСТАТКИ» состоит из 7 букв.

В нем 4 согласных и 3 гласных.

Написание следующим образом облегчает решение подобных вопросов.

(1) (2) (3) (4) (5) (6) (7)

Количество способов, которыми 3 гласных могут встречаться в 4 разных местах = ⁴ P ₃ = 24 способа.

После 3 гласных занимают 3 места, нет. 4 согласных могут занимать 4 места = ⁴ P ₄ = 4! = 24 способа.

Следовательно, общее количество возможных перестановок = 24*24 = 576 способов.

Комбинации

Определение
Различные варианты выбора из набора элементов называются комбинациями.

Например:

Возможны различные варианты выбора из алфавитов A, B, C, взятые по 2 за раз: AB, BC и CA.

Не имеет значения, выбираем ли мы A после B или B после A. Порядок выбора не важен в комбинациях.

Чтобы найти количество возможных комбинаций из данной группы элементов n, взятых по r за раз, формула, обозначаемая как ⁿ C _r, равна

ⁿ C _r = n! / [р! * (н-р)!]

Например, проверяя приведенный выше пример, различные возможные варианты выбора из алфавитов A, B, C, взятые по два одновременно, составляют

³ C ₂ = 3! / (2! * (3-2)!) = 3 возможных варианта выбора (т. е. AB, BC, CA)

Важно Формулы комбинаций

ⁿ C _n = 1

ⁿ C 0 = 1

ⁿ C ₁ = n

ⁿ C _r = ⁿ C _(n-r)

Количество возможных выборов с A, B, C, взятых одновременно, равно ³ C ₃ = 1 (т. е. ABC)

Решенные примеры комбинации

взгляните на несколько примеров, чтобы понять, как работают комбинации:

Задача 1: Сколькими способами можно составить комитет из 1 мужчины и 3 женщин из группы из 3 мужчин и 4 женщин?

Решение :

Количество способов 1 человек может быть выбран из группы из 3 человек = ³ С ₁ = 3! / 1!*(3-1)! = 3 способа.

Количество способов 3 женщины могут быть выбраны из группы из 4 женщин = ⁴ C ₃ = 4! / (3!*1!) = 4 способа.

Задача 2: Сколько среди набора из 5 черных и 3 красных шаров можно выбрать 5 шаров так, чтобы хотя бы 3 из них были черными.

Решение :

Выбор не менее 3 черных шаров из набора из 5 черных шаров при общем выборе из 5 шаров может быть

3 B и 2 R

4 B и 1 R и

5 B и 0 R мячи.

Таким образом, наше выражение решения выглядит так.
⁵ C ₃ * ³ C ₂ + ⁵ C ₄ * ³ C ₁ + ⁵ C ₅ * ³ C ₀ = 46 способы .

Примеры сочетания: 4.2.3. Сочетания

4.2.3. Сочетания

Глава 4. Комбинаторика

4.2.

4.2.3.

Главная Онлайн учебники База репетиторов России Тренажеры по математике Подготовка к ЕГЭ 2017 онлайн

Сочетания и их свойства примеры. Элементы комбинаторики

Размещения и перестановки

Сочетания

Разбиение множества на группы

Комбинаторика: основные правила и формулы.

СОЧЕТАНИЕ — Что такое СОЧЕТАНИЕ?

Значения слова сочетание. Что такое сочетание?

Примеры употребления слова сочетание

Пример сочетания клавиш MUI — Win32 apps

ТОП-20 лучших цветовых сочетаний | Наглядные примеры

Подбирайте цветовые сочетания в один клик в программе ФотоМАСТЕР!

ТОП-20 цветовых сочетаний: описание и примеры

Теплые сочетания

Холодные сочетания

Свежие сочетания

Темные схемы

Яркие схемы

Мягкие сочетания

Вывод

Простые перестановки и комбинации — BetterExplained

Перестановки: Волосатые детали

Комбинации, Хо!

Несколько примеров

Другие сообщения из этой серии

Комбинации — определение, формула, примеры, часто задаваемые вопросы

Что такое комбинации?

Что такое формула комбинаций?

Комбинации как выбор

Связь между перестановками и комбинациями

Каковы примеры комбинаций?

Комбинации — примеры и практические задачи

АЛГЕБРА

АЛГЕБРА

Сводка комбинаций

Комбинации – Примеры с ответами

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Комбинации – практические задачи

Найдите комбинацию $latex _{9}C_{5}$.

Найдите комбинации $latex _{11}C_{9}$.

Сколько комбинаций получится, если мы возьмем 2 предмета из набора из 7?

Мы хотим выбрать команду из 6 человек из 9. Сколько существует способов добиться этого?

На собрании 10 человек. Если все пожмут друг другу руки, сколько рукопожатий возможно?

См.

Изучайте математику с помощью наших дополнительных ресурсов по различным темам

Перестановки и комбинации: различия и примеры

Примеры перестановок и комбинаций

Формулы подсчета перестановок и комбинаций

Пример перестановки

Пример комбинации

Использование перестановок и комбинаций для решения вероятностных задач

Задачи на перестановки и комбинации

Комбинации

Задачи

решения вышеуказанных проблем

Еще Ссылки и ссылки

задач на перестановки и комбинации | GMAT GRE Учебник по математике

Перестановки

Определение

Формула факториала определяется как произведение всех чисел от n до 1.

Важные формулы перестановки

Комбинации

Определение Различные варианты выбора из набора элементов называются комбинациями.<img loading='lazy' src='' />

Определение

Важно Формулы комбинаций

Решенные примеры комбинации

Добавить комментарий Отменить ответ

Определение
Различные варианты выбора из набора элементов называются комбинациями.