Как отвязать номер своего телефона от страницы Вконтакте? Как отвязать номер от страницы в вк
Сегодня я продолжу разбирать проблемы, возникающие у пользователей социальных сетей. Проблем этих, надо заметить, великое множество: то одно не работает, то другое, то непонятно, другому пользователю… В общем, вопросов хватает и на большинство из них приходится отвечать службе поддержки. Сегодня я расскажу о том, как отвязать номер мобильного телефона от страницы в ВК.
Пользователи, которые регистрировались на проекте Павла Дурова лет пять назад, наверняка помнят еще те времена, когда привязки к телефону не было в принципе. Потом идея появилась на небольших проектах, а затем ей начали пользоваться крупные «игроки» интернет-рынка. Сейчас точно неизвестно, кто придумал этот способ (российские спецы или заграничные), но работает он великолепно. Почему? Да просто потому, что вы никогда не потеряете свой аккаунт — если телефон под рукой, всегда можно восстановить доступ к странице. Кроме того, можно сделать так, что бы вам на устройство приходили уведомления о любых изменениях, включая новые сообщения, поставленные лайки и т.п.
Кроме того, можно сделать так, что бы вам на устройство приходили уведомления о любых изменениях, включая новые сообщения, поставленные лайки и т.п.
Изначально привязка к номеру в ВК была не обязательной — можно было пользоваться соц.сетью сразу после регистрации. Но некоторое время назад произошла настоящая революция — любой аккаунт принудили привязать к телефону! Некоторые члены проекта были недовольны таким нововведением, другие же на него даже не обратили внимания… Лично я считаю, что это одна из самых гениальных задумок Дурова, ведь таким образом человек использует свой номер в качестве логина, может моментально восстановить доступ к профилю, а количество вопросов, связанных с его восстановлением, резко уменьшилось, что помогло разгрузить . В общем, одни сплошные плюсы.
Впрочем, во всей этой ситуации есть один минус — отвязать номер сегодня невозможно в принципе, вы можете только поменять его на другой, к которому у вас есть доступ. Для этого зайдите в свой аккаунт, выберите раздел «Мои настройки», опустите страницу вниз до пункта «Изменить номер телефона» и нажмите на одноименную кнопку.
Сюда пишем новый номер, ждем код на телефон и вписываем его в соответствующее поле. Все, перепривязка прошла успешна.
Что делать в том случае, если страница удалена или заблокирована? Здесь может помочь только одно — нужно написать в службу поддержки с полным описанием проблемы. Тоже самое нужно сделать в том случае, если вы пытаетесь создать новый аккаунт, а система говорит вам о том, что номер уже привязан к другой странице (такое возможно, если вы недавно обзавелись новой сим-картой). Следуйте всем необходимым рекомендациям, которые последуют от представителей поддержки и ваша проблема, я уверен, будет решена.
Если появились вопросы по статье, задавайте их — попробую вам помочь.
Как правило, злоумышленники меняют пароль странички пользователя, и владелец уже не может получить доступ к своему аккаунту. Во избежание такого печального развития событий необходимо при регистрации в социальной сети выполнять привязку страницы к почте и мобильному телефону. В этой статье разберем, как выполнить данные процедуры.
Привязка к почте
- В разделе «Общее» находим поле «Адрес Вашей электронной почты» и указываем желаемый адрес. Важно! После сохранения настроек адрес почты будет отображаться в формате с***@mail.com, то есть злоумышленник, получивший доступ к вашей странице, не сможет узнать вашу почту.
- Вы также можете настроить оповещения по электронной почте о событиях, происходящих на вашей странице в социальной сети. Для этого переходим во вкладку оповещения, находим раздел «Оповещения по электронной почте», указываем адрес электронной почты и настраиваем частоту оповещений — «Всегда оповещать» или «Оповещать не чаще раза в день».
Привязка к номеру телефона
- Заходим на свою страничку в социальной сети «ВКонтакте», кликаем по ссылке «Мои настройки».
- В разделе «Общее» находим поле «Номер вашего телефона» и указываем номер в формате +7(ХХХ)ХХХХХХХ. Важно! После сохранения настроек телефон будет отображаться в формате +7 *** *** ** 18, то есть злоумышленник, получивший доступ к вашей странице, не сможет узнать ваш мобильный номер.
- Вы также можете настроить оповещения по телефону о событиях, происходящих на вашей странице в социальной сети. Для этого переходим во вкладку оповещения, находим раздел «Оповещения через SMS» и ставим галочку в окошке «Получать SMS-оповещения».
Интересно, что на оповещения можно ответить, то есть если какой-то пользователь прислал вам личное сообщение «ВКонтакте», вы можете ответить ему посредством SMS, однако ответ придет ему также в профиль социальной сети. Однако помните, что оповещения бесплатны, а за ответы придется заплатить. Тариф определяется оператором. Информацию о стоимости SMS для вашего конкретного случая можно узнать во вкладке «Мобильные сервисы» меню «Мои настройки» социальной сети.
Уже взломали
Если вас взломали в социальной сети и сменили вам пароль, а привязку ни к почте, ни к телефону вы не выполнили, то вам нужно будет написать письмо в Службу поддержки сайта, заполнив специальную анкету, в которой, в частности, потребуется указать паспортные данные. Кроме того, наберитесь терпения, ждать ответа поддержки придется 2-3 недели.
Кроме того, наберитесь терпения, ждать ответа поддержки придется 2-3 недели.
как привязать в вк свой номер к другой странице,если даже…
- я согласна с анастасией, как привязать к новой странице номер, который был когда то на удаленной страничке вк
- Что делать? Когда я пытаюсь привязать страницу к номеру, выбывает рамка, что этот номер уже использован ранее… Что делать? Если страница не привязана вообще к телефону и нельзя писать сообщения в вк или что либо делать? Как привязать страницу к номеру к которому уже была привязана другая страница? Прошу помогите!!
- У меня 2 страницы. Одну я удалила, а вторую не могу привязать к номеру. Что надо делать?
- такая-же проблема, но у меня немного другое. У меня была страница с привязанным номером, и я решил создать вторую, создал привязал к ней номер (тот же, что и к первой и вс получилось), однако когда я лайкнул коммент с первой страницы мне выдало то, что нет привязанного номера, удалил страницу (вторую) не помогло.

- Сеть Вконтакте развивается стремительно, охватывает все больше и больше стран и людей. В ней зарегистрированы десятки миллионов человек. В связи с таким огромным количеством участников встает вопрос о безопасности — как сохранить свои личные данные? Как сделать недоступными для посторонних ваши фотографии и сообщения? Как защитить страницу от спамеров?
Как привязать номер к страницеНеобходимо сначала зайти в раздел «Настройки». Во вкладке «Общее» внизу страницы найти строку «привязать номер телефона» и вписать в нее ваш номер, которым вы будете пользоваться для этой страницы. После чего вы получите код в виде смс на указанный вами телефон. Код вписываете в специальную строку в вконтакте. Номер привязан!
Однако бывает, что для выполнения каких-то опций в сети вам нужно вводить привязанный ранее к странице телефон.
 А как быть, если вы его случайно забыли или у вас несколько страниц и вы не помните, где какой номер привязывали? То есть как узнать привязанный номер вконтакте?
А как быть, если вы его случайно забыли или у вас несколько страниц и вы не помните, где какой номер привязывали? То есть как узнать привязанный номер вконтакте?Заходим снова в Настройки, выбираем вкладку «Общее». Внизу страницы в строке «текущий номер» отображается ваш номер телефона. Но видно его не целиком, некоторые цифры заменены звездочками. Чтобы посмотреть его полностью, нажмите кнопку ниже «изменить номер телефона».
Здесь же при необходимости вы сможете сменить номер на другой. Но сначала на текущий номер придет смс с кодом, вы должны ввести его для подтверждения и ваш номер поменяют.
Если Вы хотите восстановить вашу страницу, а номер, к которому она привязана, был утерян, то необходимо связаться со службой поддержки по ссылке восстановление страницы и ввести достоверные данные.
- страничку удалить
О том, как привязать страницу в ВК к другому номеру говорят часто, но не все способы работоспособны. Социальная сеть — площадка для получения прибыли предпринимателями и фрилансерами, поэтому уровни защиты растут в геометрической прогрессии.
Существующие способы
Есть три официальных метода, как привязать страницу ВК к телефону.
#1. Изменить в настройках
Вы имеете право изменять свои персональные данные, хотя возможности и ограничены. Описываемый способ требует ожидания согласия модераторов ВК в течение двух недель.
- Зайдите в настройки аккаунта, кликнув по аватарке вверху справа.
- Щелкните ссылку «Изменить» напротив номера. В целях безопасности его большая часть отображается звездочками.
- Введите новое значение. Если телефон уже используется, вы получите предупреждение. Также увидите сообщение, если введенный номер уже использован другим профилем. В сообщении отображается число доступных привязок.
- Подтвердите действие по коду.
Заявка будет сформирована и отправлена администраторам сети. В течение 14 дней вы получите ответ.
#2. Блокировка аккаунта
Способ действенный, но, с другой стороны — опасный. Профиль пользователей ВК, неоднократно нарушавших правила, замораживается навсегда. При «разморозке» можно указать новый мобильный. Подтверждается он кодом.
Профиль пользователей ВК, неоднократно нарушавших правила, замораживается навсегда. При «разморозке» можно указать новый мобильный. Подтверждается он кодом.
Чтобы попасть в бан, проявите запрещенную активность – подписывайтесь, ставьте лайки. Оставьте свой идентификатор на биржах лайков. Разместите пост с ссылкой на такой ресурс. Блокировка произойдет в течение короткого времени.
#3. Перепривязать номер
Привязать номер телефона к странице в ВК, если он привязан к другой возможно, сначала потребуется его Вам потребуется подтвердить его легитимность с помощью кода доступа, который придет в виде смс. Можно действовать через настройки или восстановление доступа к своему профилю.
Итак, что делать, если номер телефона привязан к другой странице в ВК:
- Введите в строке адреса vk.com/restore .
- Кликните ссылку ниже формы: для тех, кто не помнит данных и не имеет доступа к телефону.
- Введите старые данные и укажите новый мобильный.

- Подтвердите кодом.
«Что делать, если не получается, и я не могу привязать к странице ВКонтакте номер своего телефона?», — это частый вопрос пользователей. Решать такой вопрос необходимо на уровне администратора. Вероятность получить положительный ответ мала, так как необходимо дать подробные и правдоподобные разъяснения причин.
Как часто можно пользоваться этими способами?
Выполнять вышеуказанные действия постоянно не получится. Через сколько можно привязать номер к другой странице ВКонтакте, зависит от частоты подобных действий. При регистрации изменить мобильный получится через сутки.
Один и тот же телефон перепривязывать можно с частотой в три-четыре месяца. Если вы исчерпали количество доступных привязок, то ждать придется годами, пока профиль не перейдет в разряд неактивных.
Знаете другие способы, как указать новый мобильный в своем профиле? Пишите в комментариях!
Социальной сетью ВК пользуется достаточно много людей, с самыми разными целями, но каждый из нас в процессе применяет свой телефонный номер. Не исключено, что в последствии могут произойти любые ситуации, которые спровоцируют необходимость отвязать номер страницы. В данной статье мы рассмотрим есть ли возможность просто так отвязать номер от своего аккаунта и принцип отвязки.
Не исключено, что в последствии могут произойти любые ситуации, которые спровоцируют необходимость отвязать номер страницы. В данной статье мы рассмотрим есть ли возможность просто так отвязать номер от своего аккаунта и принцип отвязки.
Быстрая навигация:
Отвязать номер страницы ВК
Несмотря на то, что многие пользователи задаются вопросом как отвязать номер страницы, и как можно отвязать телефонный номер от заблокированной страницы ВК, администрация Вконтакте предлагает только один вариант — замену на другой. Просто отвязать телефонный номер от страницы нельзя. Таковы принципы политики безопасности Вконтакте. Кроме этого, существует возможность отвязать номер телефона от одной страницы и привязать его к другой. Далее мы рассмотрим весь процесс отвязки и привязки поэтапно.
Как отвязать номер от страницы Вконтакте
Для того, чтобы отвязать страницу понадобится новый номер. При этом, желательно, чтобы у вас имелся доступ к двум сим картам, новой и старой. Это значительно ускорит и облегчит процесс. Прежде чем начать исследовать как отвязать номер от страницы, можно поговорить о том, как отвязать номер от страницы вк с телефона, планшета или любого другого устройства. Все действия выполняются идентично и каждое из них нужно осуществлять в настройках меню. Далее можете читать и одновременно выполнять отвязку страницы.
Это значительно ускорит и облегчит процесс. Прежде чем начать исследовать как отвязать номер от страницы, можно поговорить о том, как отвязать номер от страницы вк с телефона, планшета или любого другого устройства. Все действия выполняются идентично и каждое из них нужно осуществлять в настройках меню. Далее можете читать и одновременно выполнять отвязку страницы.
Переходим на свою страницу, и заходим в настройки. Находим подраздел «Номер телефона», и кликаем там ссылку «Изменить», переходим на изменение номера телефона, вводим новый номер телефона и просим получения кода на номер. После введения полученного кода система оповестит вас о принятие заявки на смену номера.
Процесс можно значительно ускорить, если у вас имеется доступ к старому номеру. Для этого нужно нажать на соответствующую ссылку, которая есть в форме для смены. Нажав на ссылку вам придет пароль, который также нужно ввести в окошко.
После выполнения этой процедуры номер будет изменен.
Как отвязать номер от страницы вк 2018
Все вышеописанные действия применимы и помогут сменить номер в новой версии сайта ВК, и на протяжение 2018 года можно смело использовать этот процесс для того, чтобы отвязать номер страницы.
Как отвязать номер от страницы вк и привязать к другой
Перед некоторыми обывателями встает вопрос о том, как привязать номер телефона, который задействован на другом аккаунте. Это процесс еще более прост и доступен, чем предыдущий. Если вы решили зарегистрировать новую страницу, а номер у вас всего один, вы свободно можете при регистрации новой страницы указывать тот, который уже задействован. При этом администрация предупредит вас о том, что номер уже привязан и задаст вопрос уверенны ли вы в том, что желаете применить использование номера к новой странице? Дав положительный ответ, номер будет работать уже на новой странице, а от старой отвяжется автоматически. Теперь вы знаете как можно отвязать номер от страницы вк и привязать к другой.
Как отвязать номер от заблокированной страницы вк
Даже если ваша страница Вк заблокирована все равно сохраняется возможность для отвязки номера от страницы. Администрация Вконтакте в редких случаях сразу блокирует аккаунт навсегда. Сначала приходит предупреждение, постепенно меры наказания увеличиваются: обычная заморозка, через код телефона, более длительная заморозка разблокируется только через 3 дня с использованием кода телефона. Безвозвратный бан странички — последняя мера наказания — это крайняя мера, когда вы систематически пренебрегаете правилами и раз за разом получаете блокировку страницы.
Сначала приходит предупреждение, постепенно меры наказания увеличиваются: обычная заморозка, через код телефона, более длительная заморозка разблокируется только через 3 дня с использованием кода телефона. Безвозвратный бан странички — последняя мера наказания — это крайняя мера, когда вы систематически пренебрегаете правилами и раз за разом получаете блокировку страницы.
Во время работы в онлайне, в случае если вы зарабатываете в общественных сетях, блокировка не редкость. И в случае если обстановка так масштабна, что страничку всецело заблокировали, значит придется отыскивать прием как отвязать страничку вк от номера телефонного аппарата. К счастью, присутствует достаточно незатейливый прием это сделать. Для данных целей вам необходимо сделать новенькую страницу, и прикрепить к ней номер, применяемый на заблокированном аккаунте. После доказательства кодом номер отвяжется от заблокированной странички, и привяжется к свежему чистому аккаунту. Так просто! Теперь вы знаете как отвязать номер от заблокированной страницы вк и привязать новый:
- Зарегистрируйте новейший аккаунт, указав старый номер, который был привязан к заблокированной страничке.

- Утвердите права на номер телефонного номера, введя подтверждающий код.
- Получите новейший аккаунт, где будет привязан ваш старый номер.
Симка с новым номером…
Когда необходимо высвободить всецело номер, в тех случаях вам понадобится симка с новым номером, который не привязан ни к какому аккаунту в ВК. Повторите выше обозначенные деяния, описанные в аннотации, чтоб заменить привязанный номер на странице. В конце у вас будет аккаунт, привязанный к новенькому номеру, и старый номер, который ни к чему не привязан. Таким же образом легко понять как отвязать номер от удалённой страницы вк. Все выполняется тем же способом. Также отвязав номер от удаленной страницы можно привязать его к новому аккаунту.
Несмотря на то, что все так радужно, важно знать, что телефон особо злостных нарушителей могут добавить в черный список, и на этот номер нельзя будет завести в дальнейшем новый аккаунт. Имейте в виду, что руководство Вконтакте не одобряет частый переход одного номера между несколькими страницами. Так что не рассчитывайте на возможность каждый день привязывать номер к новому аккаунту — есть ограничения.
Так что не рассчитывайте на возможность каждый день привязывать номер к новому аккаунту — есть ограничения.
В данном посте мы подробно рассмотрели о том, как отвязать номер страницы в разных вариантах.
2 способа отвязать свой номер телефона от страницы Вконтакте
Вконтакте – самая популярная социальная сеть. Ежедневно создаются и удаляются более сотни аккаунтов. Естественно при уничтожении своего профиля в сети Интернет, захочется подчистить за собой как можно больше доступных хвостов. Именно поэтому в данной статье мы проиллюстрируем алгоритм отвязки номера от профиля ВК.
Содержание
- 2 способа отвязать свой номер телефона от страницы Вконтакте
- Способ 1: Отвязать страницу Вконтакте официальным способом
- Способ 2: Отвязать номер от аккаунта ВК с помощью бага
Порой случаются ситуации, когда необходимо отвязать свой номер телефона от Вконтакте. Раньше для этого необходимо было всего лишь прикрепить электронную почту к аккаунту. Однако теперь этого недостаточно. Групповая политика безопасности Вконтакте обязывает привязывать к аккуанту номер телефона пользователя для предотвращения хакерских нашествий.
Однако теперь этого недостаточно. Групповая политика безопасности Вконтакте обязывает привязывать к аккуанту номер телефона пользователя для предотвращения хакерских нашествий.
Что вам необходимо знать о групповой политики ВК? Так это только то, что номер телефона может быть привязан только к одной странице Вконтакте. Это чревато тем, что при утере старой страницы или для создания новой под этот номер, необходимо для начала отвязать номер от предыдущего аккаунта. Итак, приступим к рассмотрению двух способов, как этого можно добиться.
Способ 1: Отвязать страницу Вконтакте официальным способом
На самом деле официальный метод подразделяется на два варианта, позволяющих отвязать телефон, доступа к которому нет и тот, к которому имеется. Во втором случает для отвязки номера потребуется одни день, в первом же четырнадцать календарных дней. Чтобы упростить процесс до двух дней, потребуется документ подтверждающий личность. Итак, разберем всё по порядку.
Для начала проиллюстрируем, как привязать электронную почту к аккаунту. Однако, если раньше с помощью этого можно было отвязать номер телефона, не добавляя новый, то в 2018 году такое уже не пройдет.
Однако, если раньше с помощью этого можно было отвязать номер телефона, не добавляя новый, то в 2018 году такое уже не пройдет.
В тоже время привязка почты может быть полезна при утере доступа к старой сим-карте. Им можно воспользоваться для восстановления доступа к аккаунту, также и для изменения привязанного телефона на новый, к которому больше нет доступа.
- Откройте настройки аккаунта ВК. Напротив графы «Электронная почта» нажмите «Добавить».
- Укажите адрес электронной почты, который будет привязан к странице.
- Для отправки сообщения на почту, введите повторно в запрашиваемое окно пароль от страницы.
- Перейдите на адрес электронной почты.
- Прочитайте письмо от ВК. Откройте ссылку, для подтверждения проделанных действий. После чего email удачно привязан.
Теперь проиллюстрируем, как работает отвязка номера телефона от аккаунта.
- Перейдите заново в настройки.
 Напротив номера телефона нажмите «Изменить».
Напротив номера телефона нажмите «Изменить». - Введите новый номер телефона, который необходимо привязать к странице.
- Далее система оповестит вас о том, что на смену пароля потребуется две недели. После чего у вас есть два алгоритма действий: ускорить процесс за счет имения доступа к старому телефону, либо процесс , подобный восстановлению пароля. Ели у вас имеется доступ, перейдите по первой ссылке. Иначе откройте пункт.
- Вам будет направленно смс с кодом на старый номер телефона.
- Введите его в графу, отвечающую за код подтверждения.
- После чего номер телефона будет успешно изменен.
- Если же у вас нет доступа к старой сим-карте, перейдите по второй ссылке.
- Именно на этом этапе пригодился бы адрес электронной почты. Но об этом позже. Внизу окна выберите ссылку, говорящую – «Нажмите сюда».
- Далее вставьте ссылку, ведущую на ваш аккаунт. Ее также можно отыскать, нажав «поиск по людям».
 Это ограниченная версия Вконтакте, позволяющая с помощью фильтра отыскать свой аккаунт.
Это ограниченная версия Вконтакте, позволяющая с помощью фильтра отыскать свой аккаунт. - После чего отобразится окно для заполнения данных, укажите всю доступную вам информацию.
- Обязательным требованием считается указание пароля, благодаря которому был воспроизведен вход. Если он по какой-то причине утерян, нажмите по предлагаемой ссылке.
- Откроется еще более расширенная версия ввода данных для подтверждения личности. Вначале введите доступный номер телефона.
- После чего прикрепите фотографию, сделанную напротив монитора с открытой заявкой на изменение номера.
- Далее прикрепите цветную фотографию документа с расположенными на нем инициалами и вашей фотографией.
- Напоследок укажите причину по которой был утерян доступ к номеру телефона.
- После нажатия кнопки «Подать заявку», ответьте на вопрос о посещении страницы за последние сутки.
- На доступный номер будет выслан смс код. Введите его в окно подтверждения.
- Система оповестит вас о том, что заявка будет рассматриваться до сорока восьми часов.
Таким образом даже не имея доступа к старой сим-карте можно сократить время изменения номера до двух дней. Конечно это не маленькое количество времени, однако и не две недели.
Отметим еще одну особенность групповой политики Вконтакте – запрещено подавать заявку на изменение номера телефона аккаунта более одного раза в сутки.
Способ 2: Отвязать номер от аккаунта ВК с помощью бага
Групповая политика Вконтакте запрещает пользователям всяческим образом накручивать лайки и подписчиков, используя сторонни сервисы. Подобные действия наказуемы блокировкой страницы на некоторый промежуток времени, однако как следствие возник баг, позволяющий в это время сократить отвязку номера от страницы до 1 дня. Проиллюстрируем алгоритм работы метода.
- В первую очередь необходимо опубликовать новость на своей стене с содержанием ссылки v-like.ru. Если кто не знает, это сервис для накрутки лайков.

- Не пройдет и минуты, как администрация Вконтакте заблокирует вашу страницу, подозревая, что доступ к ней перехватили злоумышленники. Далее вам необходимо выбрать новый номер, на который вышлется код подтверждения. Именно здесь можно указать новый номер аккаунта, который в дальнейшем будет автоматически привязан к странице. Нажмите «Указать другой номер».
- Вышлете код подтверждения на новую сим-карту.
- Подтвердите действие, означающее привязку нового идентификатора – значения, доступ к которому имеется исключительно у вас.
- Введите код подтверждения.
- После чего придумайте новый пароль к странице. Далее система вас попросит авторизоваться на сервисе не ранее, чем через один день. Однако как следствие с новыми данными можно авторизоваться сразу же после смены пароля на данном этапе.
Расскажем еще об одной хитрости – существуют сервисы, предоставляющие номера телефона на определенный срок использования, которого хватит для привязки к старой странице. Однако существует большая вероятность, что восстановление доступа к такому аккаунту не увенчается успехом. Как следствие такой подход можем посоветовать только тем пользователям, которые хотят распрощаться навсегда с прошлой страницей.
Однако существует большая вероятность, что восстановление доступа к такому аккаунту не увенчается успехом. Как следствие такой подход можем посоветовать только тем пользователям, которые хотят распрощаться навсегда с прошлой страницей.
Проиллюстрируем пример работы подобного сервиса.
- Перейдя по ссылке, выберете номер, который будете использовать.
- Вставьте его в поле изменения номера аккаунта.
- Далее нажмите по выбранному номеру на сервере временных сим-карт. Отобразятся все смс, приходящие на него. Остается только отыскать нужный код.
В итоге мы рассмотрели несколько способов, как можно отвязать телефон от страницы Вконтакте. Если действовать регламенту, то для результата действий может потребоваться до 14 дней. Однако зная определенные хитрости можно сократить это время до минимума.
Как отвязать номер от страницы ВК в 2022 году
Алевтина Зайцева 05.10.2018 Обновлено: 4.03.2020 108 комментариев
Вконтакте – популярная соцсеть, которую ежедневно посещает около 80 миллионов человек, и ежедневно количество пользователей увеличивается. У многих есть сразу несколько страниц Вконтакте, однако с принятием новой политики сайта, оформить новый аккаунт стало сложней.
У многих есть сразу несколько страниц Вконтакте, однако с принятием новой политики сайта, оформить новый аккаунт стало сложней.
Содержание
- 1 Политика ВК
- 2 Зачем откреплять номер мобильного телефона?
- 3 Как отвязать номер от страницы Вконтакте
- 4 Как отвязать номер от заблокированной страницы в ВК
Политика ВК
С 2013 года при регистрации аккаунта Вконтакте используется номер мобильного и в дальнейшем номер остается связанным с ней. Это обеспечивает дополнительный уровень защиты личных данных и возможность восстановить забытый пароль при помощи смс-сообщения. С помощью мобильного страница становится более персонифицированной, так как сайт рассчитан на, в большей части, население стран СНГ, где в большинстве стран сим-карты регистрируются при помощи паспортных данных.
Зачем откреплять номер мобильного телефона?
Из-за привязки к определенной странице, на один номер телефона можно зарегистрировать одну страницу. Данное правило введено для борьбы со спамом и накрутками. Также телефон может быть утерян, и это может представлять прямую угрозу для данных пользователя. Во всех этих случаях может возникнуть вопрос: как сменить номер телефона или как отвязать номер от ВК. Для этого существует несколько вариантов.
Данное правило введено для борьбы со спамом и накрутками. Также телефон может быть утерян, и это может представлять прямую угрозу для данных пользователя. Во всех этих случаях может возникнуть вопрос: как сменить номер телефона или как отвязать номер от ВК. Для этого существует несколько вариантов.
Как отвязать номер от страницы Вконтакте
Существует официальный способ, применение которого полностью безопасно и не грозит блокировкой страницы. Однако, при использовании этого варианта стоит учитывать, что процесс займет до 14 дней. Для изменения номера Вконтакте, следует:
- Зайти на свой аккаунт Вконтакте;
- Выбрать раздел «Настройки» – «Общее» – «Номер телефона».
- Выбрать пункт «Изменить».
- В появившемся поле указать новый мобильный.
- Появится оповещение о том, что на оба телефона отправлены смс-сообщения с кодами подтверждения.
- Вводим пароли, подтверждаем оба номера и подаем заявку. По прошествию двух недель телефон будет изменен.
Если нужно отвязать номер перед тем, как удалить аккаунт, существует эффективный и быстрый способ, который, однако, может привести к блокировке номера навсегда. Для этого можно зарегистрировать фиктивный номер в специальном стороннем сервисе, и заменить им действующий телефон для получения смс-сообщений из Вконтакте.
Также, если имеются профили, зарегистрированные при помощи электронного адреса (такой способ регистрации работал до 2013 года), попробуйте заменить на действующий или удалить номер телефона в ВК. После этого произойдет автоматическая отвязка номера от новой страницы.
Закрепление номера
Если к странице нет доступа, открепить номер можно в процессе создания нового профиля. После регистрации нового профиля на телефон придет смс-сообщение, и после введения пароля номер сразу же будет закреплен за новой страницей.
«Заморозка» страницы
Если не пугает перспектива длительной заморозки аккаунта, воспользуйтесь вариантом, основанном на баге соцсети. Он состоит в том, что при замораживании аккаунта прикрепленный к нему номер телефона сразу же открепляется. Для ускорения процесса «заморозки» необходимо произвести несложные процедуры, связанные с накруткой или распространением спама: вступить в несколько десятков групп или добавить большое количество новых друзей. После заморозки страницы, при ее обновлении видим надпись:«укажите другой номер телефона». После введения действующего телефона, система отправит на него смс с кодом проверки. Вводим пароль и система сообщает, что к этой странице прикреплен другой номер. В связи с этим система предложит отвязать номер.
Он состоит в том, что при замораживании аккаунта прикрепленный к нему номер телефона сразу же открепляется. Для ускорения процесса «заморозки» необходимо произвести несложные процедуры, связанные с накруткой или распространением спама: вступить в несколько десятков групп или добавить большое количество новых друзей. После заморозки страницы, при ее обновлении видим надпись:«укажите другой номер телефона». После введения действующего телефона, система отправит на него смс с кодом проверки. Вводим пароль и система сообщает, что к этой странице прикреплен другой номер. В связи с этим система предложит отвязать номер.
После того, как будет введен новый номер, придумываем и вводим новый пароль и нажимаем на синюю кнопку «разморозить аккаунт». Таким образом, номер изменится менее чем за 24 часа.
Привязка к электронной почте
Открепить номер телефона от профиля можно и без привязки нового номера, прикрепив к нему электронную почту. Для этого :
- Выбираем графу «Оповещения» в настройках, и в ней выбираем вариант «Привязать страницу к е-mail».

- В поле заносим электронный адрес и нажимаем клавишу «Сохранить».
- После того, как будет получено письмо с подтверждением, открепляем номер телефона, перенаправив все оповещения на электронную почту.
Главное запомнить, что теперь вход на страницу будет осуществляться с использованием почты.
Как отвязать номер от заблокированной страницы в ВК
Если же после вышеуказанных способов профиль оказался заблокирован или удален, напишите сообщение специалист техподдержки Вконтакте. В ответ придет инструкция с пошаговым описанием процесса восстановления аккаунта и рекомендациями от администрации насчет того, как отвязать номер от страницы в ВК.
Алевтина Зайцева (Написано статей: 109)
Задать вопрос
Автор аналитических статей, обзоров, руководств и инструкций. Благодаря своему образованию и опыту, Алевтина — настоящий специалист в пользовании социальными сетями и умными устройствами. Просмотреть все записи автора →
Просмотреть все записи автора →
Оценка статьи:
Загрузка…
Поделиться с друзьями:
Adblock
detector
Как посмотреть к чему привязан ВК?
Мы постоянно заходим в какие-либо сервисы и в приложения с помощью своей учётной записи ВКонтакте. К примеру, некоторые сервисы по накрутке друзей, подписчиков, лайков, раскрутке групп используют авторизацию через ВКонтакте. Как итог со временем огромное количество приложений имеет доступ к нашему аккаунту, даже если мы уже не пользуемся этими приложениями и сервисами. Поэтому иногда стоит просматривать список данных приложений и удалять их привязку из нашего аккаунта ВКонтакте. Однако многие не знают, как и где ВКонтакте просмотреть подключенные к аккаунту приложения. Разберём данный вопрос подробно.
Заходим в свой аккаунт в раздел «Настройки» — «Настройки приложений»:
Здесь мы увидим все приложения, которым мы разрешали доступ к нашему аккаунту, и которые к нему подключены.
Теперь вы можете их просмотреть и удалить, то что не нужно. Не удаляйте те, которые нужны для входа на определённые сайты, ресурсы и сервисы, которыми вы на данный момент пользуетесь.
Раз в статье упомянул сервисы по раскрутке групп и аккаунтов, то дам ссылку на один из таких сервисов — Bosslike. С помощью данного сервиса вы сможете бесплатно продвигать/раскручивать не только ваши страницы и аккаунты во ВКонтакте, но и в Одноклассниках, Youtube, Инстаграме и прочиех сервисах.
29.04.2017: Статья переписана под новый интерфейс. В новом интерфейсе ВК намного быстрее добраться до настроек подключённых приложений, поэтому статья стала краткой заметкой.
Сейчас, когда пользователь регистрируется на сайте социальной сети ВКонтакте, регистрация осуществляется с помощью мобильного телефона и ввод почты не является обязательным. Это объяснимо — в случае каких-либо действий с аккаунтом сообщения приходят именно на указанный номер телефона.
После регистрации адрес e-mail в аккаунте остается пустым. Мы настоятельно рекомендуем привязать его к почтовому ящику. Так вы, к примеру, не пропустите важное сообщение, поскольку уведомление о нем придет на вашу почту.
Мы настоятельно рекомендуем привязать его к почтовому ящику. Так вы, к примеру, не пропустите важное сообщение, поскольку уведомление о нем придет на вашу почту.
Привязать e-mail к аккаунту очень просто. Зайдите на свою страницу и нажмите «Мои настройки».
Откроется страница с настройками. Оставаясь на вкладке «Общее», опустите страничку вниз, пока не увидите пункт «Адрес Вашей электронной почты».
В окно добавляете адрес своей электронной почты, к которой имеете доступ, и нажимаете «Сохранить адрес».
После этого нужно будет ввести еще раз пароль от страницы и подтвердить его.
На почту будет отправлено письмо, в котором находится ссылка. Пройдя по ссылке, вы сможете завершить привязку к почтовому ящику.
После этого вы увидите сообщение о том, что e-mail был успешно привязан к вашей странице.
Больше от вас ничего не требуется.
Алевтина Зайцева 05. 10.2018 Обновлено: 4.03.2020
10.2018 Обновлено: 4.03.2020
Вконтакте – популярная соцсеть, которую ежедневно посещает около 80 миллионов человек, и ежедневно количество пользователей увеличивается. У многих есть сразу несколько страниц Вконтакте, однако с принятием новой политики сайта, оформить новый аккаунт стало сложней.
- 1 Политика ВК
- 2 Зачем откреплять номер мобильного телефона?
- 3 Как отвязать номер от страницы Вконтакте
- 4 Как отвязать номер от заблокированной страницы в ВК
Содержание
- Политика ВК
- Зачем откреплять номер мобильного телефона?
- Как отвязать номер от страницы Вконтакте
- Закрепление номера
- «Заморозка» страницы
- Привязка к электронной почте
- Как отвязать номер от заблокированной страницы в ВК
- Алевтина Зайцева (Написано статей: 109)
- Полезные материалы:
Политика ВК
С 2013 года при регистрации аккаунта Вконтакте используется номер мобильного и в дальнейшем номер остается связанным с ней. Это обеспечивает дополнительный уровень защиты личных данных и возможность восстановить забытый пароль при помощи смс-сообщения. С помощью мобильного страница становится более персонифицированной, так как сайт рассчитан на, в большей части, население стран СНГ, где в большинстве стран сим-карты регистрируются при помощи паспортных данных.
Это обеспечивает дополнительный уровень защиты личных данных и возможность восстановить забытый пароль при помощи смс-сообщения. С помощью мобильного страница становится более персонифицированной, так как сайт рассчитан на, в большей части, население стран СНГ, где в большинстве стран сим-карты регистрируются при помощи паспортных данных.
Зачем откреплять номер мобильного телефона?
Из-за привязки к определенной странице, на один номер телефона можно зарегистрировать одну страницу. Данное правило введено для борьбы со спамом и накрутками. Также телефон может быть утерян, и это может представлять прямую угрозу для данных пользователя. Во всех этих случаях может возникнуть вопрос: как сменить номер телефона или как отвязать номер от ВК. Для этого существует несколько вариантов.
Как отвязать номер от страницы Вконтакте
Существует официальный способ, применение которого полностью безопасно и не грозит блокировкой страницы. Однако, при использовании этого варианта стоит учитывать, что процесс займет до 14 дней.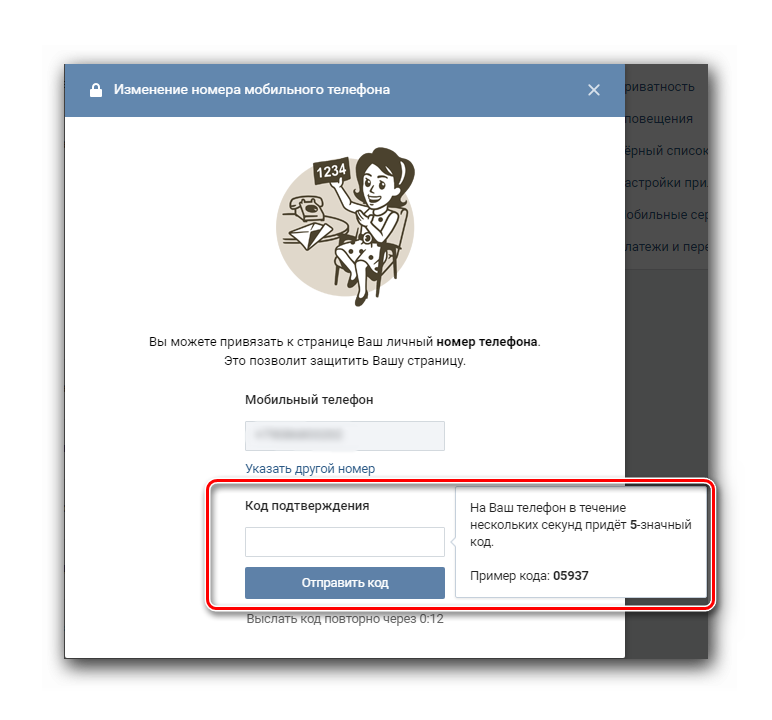 Для изменения номера Вконтакте, следует:
Для изменения номера Вконтакте, следует:
- Зайти на свой аккаунт Вконтакте;
- Выбрать раздел «Настройки» – «Общее» – «Номер телефона».
- Выбрать пункт «Изменить».
- В появившемся поле указать новый мобильный.
- Появится оповещение о том, что на оба телефона отправлены смс-сообщения с кодами подтверждения.
- Вводим пароли, подтверждаем оба номера и подаем заявку. По прошествию двух недель телефон будет изменен.
Если нужно отвязать номер перед тем, как удалить аккаунт, существует эффективный и быстрый способ, который, однако, может привести к блокировке номера навсегда. Для этого можно зарегистрировать фиктивный номер в специальном стороннем сервисе, и заменить им действующий телефон для получения смс-сообщений из Вконтакте.
Также, если имеются профили, зарегистрированные при помощи электронного адреса (такой способ регистрации работал до 2013 года), попробуйте заменить на действующий или удалить номер телефона в ВК. После этого произойдет автоматическая отвязка номера от новой страницы.
Закрепление номера
Если к странице нет доступа, открепить номер можно в процессе создания нового профиля. После регистрации нового профиля на телефон придет смс-сообщение, и после введения пароля номер сразу же будет закреплен за новой страницей.
«Заморозка» страницы
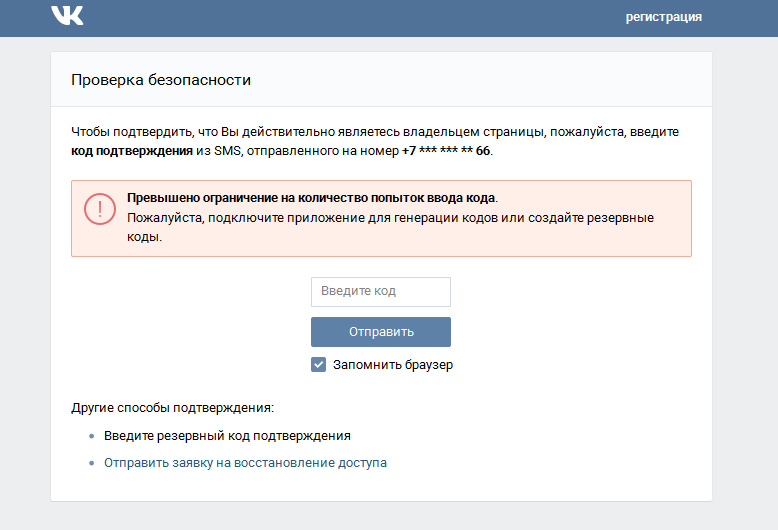
Если не пугает перспектива длительной заморозки аккаунта, воспользуйтесь вариантом, основанном на баге соцсети. Он состоит в том, что при замораживании аккаунта прикрепленный к нему номер телефона сразу же открепляется. Для ускорения процесса «заморозки» необходимо произвести несложные процедуры, связанные с накруткой или распространением спама: вступить в несколько десятков групп или добавить большое количество новых друзей. После заморозки страницы, при ее обновлении видим надпись:»укажите другой номер телефона». После введения действующего телефона, система отправит на него смс с кодом проверки. Вводим пароль и система сообщает, что к этой странице прикреплен другой номер. В связи с этим система предложит отвязать номер.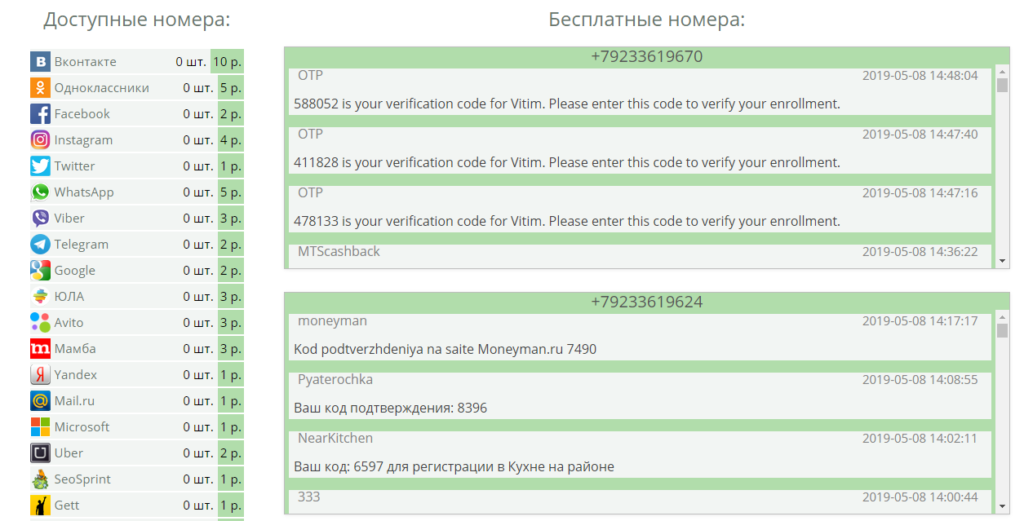
После того, как будет введен новый номер, придумываем и вводим новый пароль и нажимаем на синюю кнопку «разморозить аккаунт». Таким образом, номер изменится менее чем за 24 часа.
Привязка к электронной почте
Открепить номер телефона от профиля можно и без привязки нового номера, прикрепив к нему электронную почту. Для этого :
- Выбираем графу «Оповещения» в настройках, и в ней выбираем вариант «Привязать страницу к е-mail».
- В поле заносим электронный адрес и нажимаем клавишу «Сохранить».
- После того, как будет получено письмо с подтверждением, открепляем номер телефона, перенаправив все оповещения на электронную почту.
Главное запомнить, что теперь вход на страницу будет осуществляться с использованием почты.
Как отвязать номер от заблокированной страницы в ВК
Если же после вышеуказанных способов профиль оказался заблокирован или удален, напишите сообщение специалист техподдержки Вконтакте. В ответ придет инструкция с пошаговым описанием процесса восстановления аккаунта и рекомендациями от администрации насчет того, как отвязать номер от страницы в ВК.
Алевтина Зайцева (Написано статей: 109)
Автор аналитических статей, обзоров, руководств и инструкций. Благодаря своему образованию и опыту, Алевтина — настоящий специалист в пользовании социальными сетями и умными устройствами. Просмотреть все записи автора →
номер привязки в nLab
Пропустить навигационные ссылки | Домашняя страница | Все страницы | Последние версии | Обсудить эту страницу |
Номера связейКонтекст
Теория узлов
Теория узлов
узел , ссылка
изотопия
узел дополняет
диаграммы узлов, хордовая диаграмма
Движение Райдемайстера
Примеры/классы:
узел-трилистник
торический узел
одиночный узел
гиперболический узел
ссылка Борромео
Ссылка Уайтхеда
Звено Хопфа
Типы
простой узел
мутантный узел
инварианты узлов
пересечение номер
номер моста
номер развязывания
окрашиваемость
группа узлов
узел род?
инварианты полиномиальных узлов
(наблюдаемые непертурбативной теории Черна-Саймонса)
Многочлен Джонса
Полином ХОМФЛИ
Полином Александра
Инварианты Решетихина-Тураева
Инварианты узла Васильева
(наблюдаемые пертрубативной теории Черна-Саймонса)
Гомология Хованова
Кронштейн Кауфмана?
инварианты ссылок
Милнор мю-бар инварианты
номер привязки
Связанные понятия:
Васильев мотокотношение
Поверхность Зейферта
теория виртуальных узлов
Хирургия Дена, исчисление Кирби
объемная догадка
арифметическая топология
категория: теория узлов
Топология
топология (точечно-множественная топология, бесточечная топология)
см. также дифференциальная топология , алгебраическая топология , функциональный анализ и топологическая гомотопическая теория
также дифференциальная топология , алгебраическая топология , функциональный анализ и топологическая гомотопическая теория
Введение
Основные понятия 83
открытое подмножество, закрытое подмножество, окрестности
топологическое пространство, локаль
для топологии, база окрестности
более тонкая/грубая топология
закрытие, внутреннее, граничное
разлука, трезвость
непрерывная функция, гомеоморфизм
равномерно непрерывная функция
встраивание
открытая карта, закрытая карта
последовательность, сеть, подсеть, фильтр
сходимость
категорияTop
- удобная категория топологических пространств
Универсальные конструкции
начальная топология, окончательная топология
подпространство, частное пространство,
оптоволоконное пространство, место для крепления
пространство продукта, пространство несвязного объединения
картографический цилиндр, картографический социлиндр
картографический конус, картографический кокон
картографический телескоп
копределы нормальных пространств
Дополнительный материал, структура, свойства
красивое топологическое пространство
метрическое пространство, метрическая топология, метризуемое пространство
Пространство Колмогорова, Хаусдорфово пространство, регулярное пространство, нормальное пространство
трезвое пространство
компактное пространство, правильная карта
секвенциально компактно, счетно компактно, локально компактно, сигма-компактно, паракомпактно, счетно паракомпактно, сильно компактно
компактно сгенерированное пространство
второй счетный пробел, первый счетный пробел
сжимаемое пространство, локально сжимаемое пространство
подключенное пространство, локально подключенное пространство
односвязное пространство, локально односвязное пространство
клеточный комплекс, CW-комплекс
заостренный пробел
топологическое векторное пространство, банахово пространство, гильбертово пространство
топологическая группа
топологическое векторное расслоение, топологическая K-теория
топологический коллектор
Примеры
пустое пространство, точечное пространство
дискретное пространство, содискретное пространство
Площадь Серпинского
топология порядка, топология специализации, топология Скотта
Евклидово пространство
- реальная линия, плоскость
- цилиндр
, конус
сфера, шар
круг, тор, кольцо, лента Мебиуса
многогранник, многогранник
проективное пространство (действительное, комплексное)
место для классификации
пространство конфигурации
путь, цикл
пространства отображений: компактно-открытая топология, топология равномерной сходимости
- пространство цикла, пространство пути
Топология Зарисского
пространство Кантора, пространство Мандельброта
Кривая Пеано
линия с двумя исходными пунктами, длинная линия, линия Sorgenfrey
K-топология, пространство Даукера
Варшавский круг, пространство для гавайских сережек
Основные заявления
пространства Хаусдорфа трезвые
схемы трезвые
непрерывных образа компактных пространств компактны
замкнутых подпространства компактных хаусдорфовых пространств являются эквивалентно компактными подпространствами
открытых подпространства компактных хаусдорфовых пространств локально компактны
факторпроекции из компактных хаусдорфовых пространств замкнуты в точности, если кодовая область хаусдорфова
компактных пространства эквивалентно имеют сходящуюся подсеть каждой сети
лемма числа Лебега
секвенциально компактные метрические пространства являются эквивалентно компактными метрическими пространствами
компактных пространства эквивалентно имеют конвергентную подсеть каждой сети
секвенциально компактных метрических пространства вполне ограничены
Функция со значениями в непрерывном метрическом пространстве на компактном метрическом пространстве равномерно непрерывна
паракомпактных хаусдорфовых пространств нормальны
паракомпактных хаусдорфовых пространств эквивалентно допускают подчиненные разбиения единицы
закрытые инъекции являются вложениями
собственные отображения в локально компактные пространства закрыты
инъективных собственных отображения в локально компактные пространства эквивалентны замкнутым вложениям
локально компактные и сигма-компактные пространства паракомпактны
локально компактных и счетных до секунды пространств сигма-компактны
регулярных пространства со счетом секунд паракомпактны
CW-комплексы являются паракомпактными хаусдорфовыми пространствами
Теоремы
Лемма Урысона
Теорема расширения Титце
Теорема Тихонова
трубная лемма
Теорема Майкла
Теорема Брауэра о неподвижной точке
топологическая инвариантность размерности
Теорема о кривой Жордана
Теоремы анализа
Теорема Гейне-Бореля
теорема о промежуточном значении
теорема об экстремальных значениях
топологическая теория гомотопий
левая гомотопия, правая гомотопия
гомотопическая эквивалентность, деформационный ретракт
основная группа, покрывающая пространство
фундаментальная теорема о покрытии пространств
гомотопическая группа
слабая гомотопическая эквивалентность
Теорема Уайтхеда
Теорема Фрейденталя о подвеске
теорема о нервах
свойство гомотопического расширения, корасслоение Гуревича
последовательность cofiber
Стрём модель категории
классическая модельная структура на топологических пространствах
- Знаки пересечения
- Корчиться
- Номер привязки
- Примеры
- Инвариантность?
- Номер привязки является целым числом
На диаграмме ориентированных связей мы видим два типа возможных пересечений. Они выделяются знаком + или -.
Они выделяются знаком + или -.
Один из способов запомнить правила знаков — представить подход к перекрестку вдоль 9-й0203 подземный переход в направлении ориентации:
- если подземный переход проходит слева направо, переход считается положительным ;
- , если он проходит справа налево, он считается отрицательным .
Изгиб
Изгиб ориентированного узла или звена диаграммы представляет собой сумму знаков всех ее пересечений. Если DD — диаграмма, мы обозначаем ее изгиб через w(D)w(D).
Изгиб используется в определении некоторых инвариантов узла.
Это вариант корчи, более адаптированный для использования со ссылками.
Предположим, что у нас есть ориентированная диаграмма связей DD с компонентами C1,…,CmC_1, \ldots, C_m, число связи CiC_i с CjC_j, где CiC_i и CjC_j являются различными компонентами DD, должно составлять половину суммы признаков пересечений CiC_i с CjC_j; он будет обозначаться lk(Ci,Cj)lk(C_i,C_j).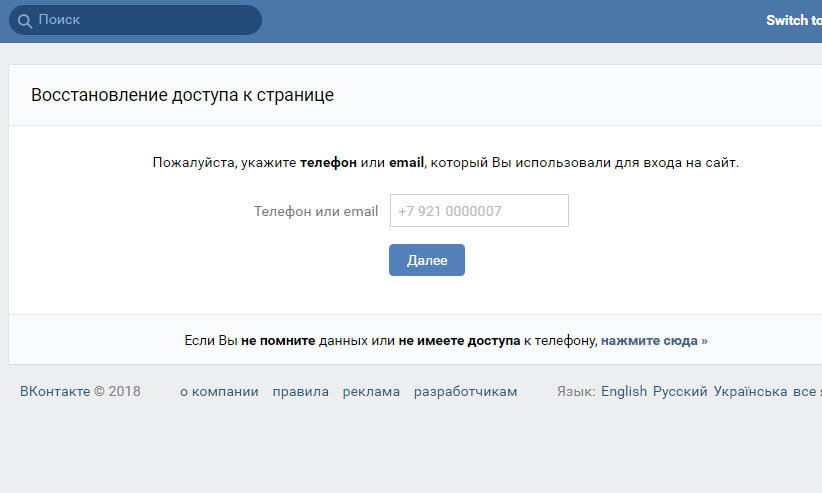
Число связей диаграммы DD тогда сумма чисел связей всех пар компонентов:
Lk(D)=∑1≤i Изгиб стандартного трилистника равен 3, звена Хопфа (оба компонента ориентированы по часовой стрелке) равно +2, а кольца Борромео равно 0, хотя это нетривиальное звено. Корч не является изотопическим инвариантом, так как его можно изменить, а скрутить стойку узла (или звена). Корч является инвариантом регулярной изотопии. Номер ссылки является инвариантом ссылки. Мы используем движения Рейдемейстера, поэтому необходимо проверить, не изменяют ли они номер связи диаграммы. Любое движение Рейдемейстера, которое включает по крайней мере два компонента связи (т. е. которое должно быть R2 или R3), оставляет все номера связей между компонентами неизменными. Ход R2 удаляет или вводит два перекрестка противоположного знака, в то время как ход R3 оставляет число пересечений и их знаки неизменными. Мы можем заключить, что зацепление Хопфа не изотопно двухкомпонентному разъединению (что обнадеживает), поскольку любое присвоение ориентации зацеплению Хопфа приводит к ненулевому числу зацеплений. Пусть n1n_{1} (соответственно n2n_{2}) будет суммой знаков пересечений между парой компонент L1L_{1} и L2L_{2} звена, в котором наддуга принадлежит L1L_{1 } (соответственно L2L_{2}). Таким образом, связующее число явно равно 12(n1+n2)\frac{1}{2}(n_{1} + n_{2}). Теперь возьмем пересечение между L1L_{1} и L2L_{2} так, чтобы дуга над дугой принадлежала L1L_{1}. Предположим, что мы переключили тип пересечения, так что теперь нижняя дуга принадлежит L1L_{1}. Тогда, независимо от знака пересечения, можно проверить, что сумма n1−n2n_{1} — n_{2} не меняется при этом переключении. Очевидно, что мы также можем переключать пересечения на самопересечения компонента или на пересечения двух рассматриваемых компонентов с другими компонентами, не затрагивая сумму n1−n2n_{1} — n_{2}. Кроме того, несложно проверить, что движения Рейдемейстера не изменяют сумму n1−n2n_{1} — n_{2}. Теперь очевидно, что любая пара компонентов ссылки может быть отсоединена от ссылки после выполнения соответствующих перекрестных переключений. В случае, когда L1L_{1} и L2L_{2} представляют собой окружности, не пересекающиеся друг с другом и с остальной частью звена, мы имеем, что n1−n2=0n_{1} — n_{2} = 0, Мы заключаем, что n1−n2=0n_{1} — n_{2} = 0 во всех случаях. Следовательно, n1=n2n_{1} = n_{2}, а число связей равно 12(2n1)=n1=n2\frac{1}{2}(2n_{1}) = n_{1} = n_{ 2}. В частности, номер ссылки является целым числом. Непосредственным следствием того факта, что сумма знаков пересечений между L1L_{1} и L2L_{2} четна, является то, что на самом деле должно быть четное число таких пересечений. Последняя редакция: 7 июня 2017 г., 15:09:44.
См. историю этой страницы для получения списка всех вкладов в нее. Связующее число является топологическим свойством ДНК. Связующее число — это сумма завихрений и корчей. Количество раз, когда одна нить ДНК оборачивается вокруг другой, называется поворотом, а взаимное закручивание двойной спирали называется корчей. Короче говоря, извитость — это количество раз, когда двойная спираль ДНК пересекается, накручивается друг на друга или количество раз, когда одна нить оборачивается вокруг другой. Согласно модели Уотсона и Крикса, эукариотическая ДНК является правозакрученной и имеет отрицательную суперспирализацию. Очень сложно понять топологию ДНК в двумерном пространстве, потому что топология — это наука, которую нельзя понять без свойства трехмерности. Чтобы понять номер привязки, мы можем предположить намотку модели телефонного провода. Тот же образец ДНК следует во время упаковки или суперспирализации. Подробнее об упаковке ДНК читайте в статье Упаковка ДНК у эукариот. Корчание ДНК более важно, так как это поможет в расположении ДНК. Здесь корчи могут быть перекручены или перекручены. Переплетенные корчи являются плектонемическими, что означает, что они наматываются друг на друга или вокруг оси. При перекрутке корчится по спирали. Классическим примером спиральной намотки является сборка гистонов и ДНК, дцДНК закручивается вокруг гистонов по спирали во время образования нуклеосом. Ключевые темы: Сумма общего количества изгибов и корчей называется числом связывания. Если оба конца ДНК соединены, число связей остается неизменным (число связей равно нулю в случае кольцевой молекулы ДНК). Итак, если мы хотим изменить номер связи, мы должны разорвать цепь ДНК, и эту функцию выполняет ДНК-топоизомераза. Важно отметить, что скручивание и скручивание могут быть взаимопреобразовываемыми, в cccDNA при некоторых условиях искажения некоторые скручивания могут быть преобразованы в скручивания, а некоторые из скручиваний могут быть преобразованы в скручивания. Однако сумма обоих остается неизменной (поскольку Lk = Tw + Wr). Эукариотическая ДНК имеет форму В, правостороннюю и недозакрученную, что означает, что она имеет отрицательную сверхспирализацию. Левосторонняя ДНК положительно сверхспиральна и перекручена (не распространена в природе). Позже в этой части мы обсудим, почему важна отрицательная суперспирализация. При сверхспирализации ДНК извитость также зависит от крутки. Как мы знаем, скручивание зависит от осевого напряжения ДНК, когда число скручиваний увеличивается, это увеличивает торсионное напряжение на оси ДНК, и в конечном итоге скручивание будет увеличиваться. В кзкДНК корчи остаются нулевыми, так как между двухцепочечными ДНК не наблюдается взаимная спираль. здесь, если, Lk= Tw + Wr Для кзкДНК (writhe равно нулю) Итак, Lk= Tw. Изображение предоставлено: http://www.siumed.edu, изображение представляет собой количество связывающих молекул ДНК. на изображении a, Lk=1 и на b, Lk=6 Теперь представьте, что кзкДНК полностью релаксирована, что означает, что она не имеет суперспирализации, в этом состоянии число связывания становится равным нулю, поэтому сверхспирализация в кзкДНК обозначается как Lk 0 . Согласно модели Уотсона и Крика, двухцепочечная ДНК имеет 10,5 п.н. на спираль и является релаксированной. Расслабленная кзкДНК имеет в общей сложности 1050 п.н., поэтому общее число связей равно 9.0003 Число связей (Lk) = общее количество оснований/пар оснований на виток спирали следовательно, Lk= 1050 п. Lk= +100 (поскольку ДНК не является формой B и левосторонняя) Подробно указано, что если наша ДНК левосторонняя и имеет 10,5 п.н. на виток при длине 1050 п.н., то одна цепь перекрещивается или наматывается (положительная сверхспирализация) на другую нить 100 раз. Однако это всего лишь предполагаемый пример, поскольку полностью релаксированной ДНК (или положительно сверхскрученной ДНК) в природе не существует. Когда мы многократно уменьшаем изгибы и корчи, разрезая ферментом, число связей постепенно уменьшается и становится равным нулю. Следовательно, разность между номером связи (Lk) и нулевой связью (Lk 0 ) называется разностью связи ΔLk, Итак, ΔLk = Lk – Lk 0 Если значение ΔLk отлична от нуля ( >0 или <0 ), то ДНК называется сверхскрученной. Кроме того, Lk меньше, чем Lk 0 (число связей меньше нуля), ΔLk также <0, а значение, которое мы получаем, отрицательное, поэтому ДНК называется отрицательно сверхскрученной. Аналогично, если Lk > Lk 0 , то ΔLk > 0, и полученное значение положительно, поэтому ДНК называется положительно сверхскрученной. Здесь значение ΔLk зависит от длины ДНК. Если длина увеличивается, сверхспирализация будет увеличиваться, и наоборот. Специфические различия в связывании являются еще одним важным свойством сверхспирализации. Ее также называют суперспиральной плотностью, которая представляет собой разницу между разностью связей (ΔLk) и количеством связей кзкДНК (Lk 0 ). Итак, Сверхспиральная плотность = ΔLk /Lk 0 Электрофорез в агарозном геле — это метод, с помощью которого мы можем идентифицировать различные формы молекул ДНК. Если у нас есть четыре молекулы ДНК одинаковой длины с разной топологией, каждая молекула по-разному мигрирует в агарозном геле. Предположим, что первая ДНК имеет тесную кольцевую форму без суперспирализации, а вторая молекула ДНК имеет обе цепи, скрученные вокруг друг друга, что означает линейную двухцепочечную ДНК. В каждом случае молекулы ДНК мигрируют по-разному. Более компактно суперскрученная ДНК быстрее мигрирует в геле. Следовательно, четвертая (сверхскрученная и компактная) мигрирует быстрее по сравнению с другой ДНК (дорожка C и D: полоса в основании). Изображение предоставлено: «Молекулярная биология гена», 7-е издание Watson. Изображение представляет миграцию различных молекул ДНК под гелем. Первая, кольцевая ДНК, не имеет суперспирализации, поэтому мигрирует медленнее, чем любая другая ДНК, и остается последней (дорожки A и D). Чем компактнее ДНК, тем легче она проходит через поры агарозы. Таким образом, кольцевая ДНК остается последней, линейная ДНК покрывает большее расстояние, чем кольцевая ДНК, а спиральная ДНК покрывает большее расстояние, чем линейная ДНК. Наконец сверхспиральная ДНК преодолевает большее расстояние, чем любая другая ДНК, и работает быстрее. Подробнее: Что такое ккДНК? — ккДНК против кзкДНК. Топологические свойства, особенно количество связей ДНК, являются очень важными свойствами ДНК, если она не поддерживается должным образом in vivo , ДНК не может быть правильно упакована на хромосоме, что приведет к эпигенетическим изменениям и нарушению репликации. Число связей ДНК можно рассчитать с помощью приведенной выше формулы, не стесняйтесь комментировать здесь и дайте мне знать, как числа связей могут быть полезны для диагностики заболеваний. Измерение топологии по динамике путем получения числа Черна из номера привязки Скачать PDF Скачать PDF Связь с природой том 10 , Номер статьи: 1728 (2019)
Процитировать эту статью 10 тыс. 97 цитирований 3 Альтметрика Сведения о показателях Известно, что целочисленные топологические индексы, характеризующие нелокальные свойства квантовых состояний материи, непосредственно предсказывают робастные физические свойства равновесных систем. Число Черна, например, определяет квантованную холловскую проводимость изолятора. Используя невзаимодействующие фермионные атомы в оптической решетке с периодическим возбуждением, здесь мы экспериментально демонстрируем, что число Черна определяет также далекую от равновесия динамику квантовой системы. В последнее время большое внимание уделяется топологической квантовой материи, потому что она представляет собой совершенно новый класс квантовых фаз и имеет потенциальные применения, начиная от точных измерений и заканчивая квантовой обработкой информации и спинтроникой 1 . Эти фазы характеризуются отсутствием нарушения симметрии и локального параметра порядка и поэтому не подпадают под общепринятую классификацию фазовых переходов. Ультрахолодные квантовые газы являются многообещающей экспериментальной платформой для изучения этих эффектов. С одной стороны, они позволяют реализовать топологически нетривиальные зонные структуры и искусственные калибровочные поля 2,3,4,5,6,7,8,9 , а с другой стороны экспериментально доступны типичные временные масштабы для динамических исследований . Например, реализованы парадигматические топологические ленточные модели: модель Хофштадтера, описывающая решетку с суммарным магнитным потоком, и модель Холдейна на сотовой решетке, которая содержит топологически нетривиальные полосы даже при отсутствии суммарного магнитного потока. Более того, они открывают перспективу объединения этих эффектов с сильными взаимодействиями (см., например, ссылки 9).0826 10,11,12 ), которые можно настроить самостоятельно. В системах с холодным атомом число Черна было измерено для модели Хофштадтера 13 с использованием транспортных измерений и для модели Холдейна с использованием квантованного кругового дихроизма 14 . Здесь мы экспериментально исследуем увлекательную связь между топологическими свойствами основного состояния и его далекой от равновесия динамикой после сильного гашения топологически тривиальной системы, которая была недавно предложена в работе. 15 . Томография состояния выявляет два вида вихрей в импульсном пространстве: (i) статические вихри, указывающие на точки Дирака, и (ii) динамические вихри, которые появляются и исчезают парами и очерчивают замкнутый контур 16 . Охватывает ли этот контур один из статических вихрей или нет, это топологический индекс (называемый числом зацепления), который напрямую соответствует числу Черна в основном состоянии гамильтониана после закалки 15 (см. рис. 1). Мы экспериментально получаем доступ к этому топологическому индексу для топологически нетривиальных систем. Кроме того, используя это соответствие, мы наносим на карту фазовую диаграмму сконструированной Флоке модели решетки типа Холдейна, характеризуемой различными числами Черна. Иллюстрация связывающего ряда динамических вихрей. На рисунке показаны зона Бриллюэна (шестиугольник) и траектории фазовых вихрей импульсного пространства. Можно определить связующее число между статическими вихрями (прямая зеленая линия) и контуром динамического вихря (серая заштрихованная линия). Связующее число равно нулю на левой панели и единице на правой панели, что может быть напрямую сопоставлено с числом Черна основного гамильтониана (показанного сферой и тором). Исходный гамильтониан предполагается топологически тривиальным на протяжении всей рукописи, что обеспечивается за счет старта со статической оптической решеткой, в которой симметрия обращения времени не нарушается Полный размер Начнем с гексагональной оптической решетки 18 с двумя подрешетками A и B , которые связаны ближайшими (NN бор-соседями) элементы матрицы туннелирования J AB и имеют потенциальное смещение Δ AB (см. (1) где \(\hat a_l\) и \(\hat n_l\) обозначают оператор уничтожения и числовой оператор для фермиона на узле l , а 〈 l ′ l 〉 обозначает пара ближайших сайтов. Экспериментальная реализация топологических зон в управляемых оптических решетках. a Три лазерных луча (красные стрелки) интерферируют под углом 120° и образуют шестиугольную оптическую решетку. Геометрию можно настроить с помощью поляризации решетчатых лучей с помощью двух волновых пластин (серые линии). Решетку можно ускорять по круговой траектории, модулируя фазы лазерных лучей решетки. b Иллюстрация модели сильной связи голой решетки (слева) и эффективного гамильтониана для управляемой решетки (справа). Перенормированные туннельные элементы возникают из-за частоты сотрясений ω и амплитуды сотрясений α . Сдвиг подрешетки в эффективном гамильтониане можно настроить с помощью расстройки встряхивания δ Встряхивания решетки 2,3,4,5,6,7,8,19,20,21,22, 23,24,25 индуцируем круговую силу инерции с угловой частотой \(\omega = \Delta _{AB}/\hbar — \delta\) и амплитудой \(F = \alpha \hbar \omega /a\) , с небольшой отстройкой 92/\hbar \omega\) (см. Топологическая фазовая диаграмма. Расчетная фазовая диаграмма типа Холдейна возбужденной гексагональной решетки с областями с разными числами Черна (параметры: ω = 2 π ⋅ 6410 Гц, α = 1,28, отстройка δ варьируется изменением начального смещения Δ AB 7 через глубину решетки). Эксперименты выполнены при круговом встряхивании (вдоль серой линии, а также для серой точки в области C = −1). Параметры Δ AB и J AB для различной глубины решетки см. Полноразмерное изображение В этой двухзонной модели гамильтониан и эволюционирующие во времени моды могут быть визуализированы на сфере Блоха для каждого квазиимпульса. Гамильтониан является диагональным относительно квазиимпульса k и может быть записан в виде $${\mathbf{h}}({\mathbf{k}}) = h_0({\mathbf{k}}) + {\mathbf{\sigma}} \cdot {\mathbf{h}}({\mathbf{k}}).$$ (3) Здесь h ( k ) играет роль связь магнитного поля через вектор матриц Паули σ до степени свободы псевдоспина 1/2, которая натянута на два состояния подрешетки и представлена единичным вектором ψ ( k ) на сфере Блоха. Он индуцирует k -зависимую динамику прецессии с угловой скоростью \(2|{\mathbf{h}}({\mathbf{k}})|/\hbar\) вокруг себя. Его направление \mathbf{k}})|\) определяет два собственных состояния с блоховскими векторами \(\psi_{\pm} ({\mathbf{k}}) = \mp \widehat {\mathbf{h}}({\mathbf {k}})\), образующая обе блоховские полосы и, следовательно, полностью характеризующая топологию системы. Чтобы получить доступ к топологии нашей системы, мы используем схему томографии состояния, которая была введена в исх. 29 и продемонстрировано в исх. 8 . Здесь нас интересует динамика состояния после закалки между двумя гамильтонианами h i ( k ) и h f ( k ) и использование томографии состояния с временным разрешением 16 , который включает проекцию на томографический гамильтониан h t ( k ), т.е. протокол двойного гашения, как показано на рис. 4 для особого случая h t ( Примеры
Инвариантность?
Предложение
Предложение
Доказательство

Топология ДНК.
 Что такое число связей ДНК?
Что такое число связей ДНК? siumed.edu
siumed.edu
Изображение представляет собой сверхспирализацию телефонного провода. siumed.edu. Изображение представляет число связей в отрицательной суперспирализации и положительной суперспирализации.
siumed.edu. Изображение представляет число связей в отрицательной суперспирализации и положительной суперспирализации. Это изменение делает ДНК сверхскрученной и еще более плотной упакованной на хромосоме.
Это изменение делает ДНК сверхскрученной и еще более плотной упакованной на хромосоме.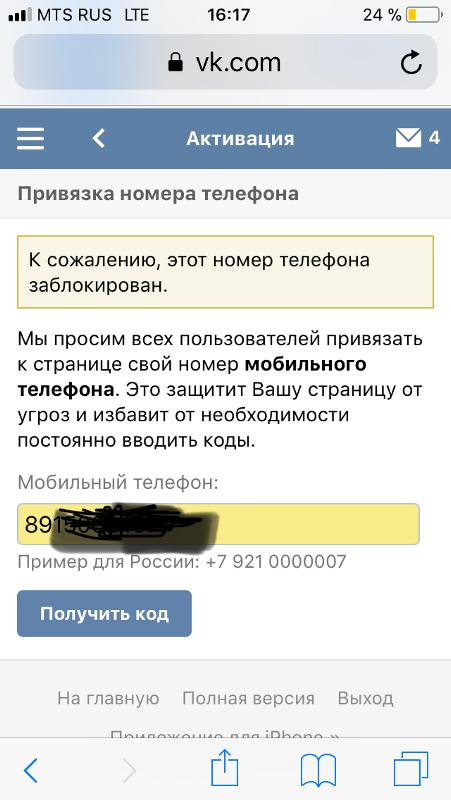 н. / 10,5 (п.н./виток)
н. / 10,5 (п.н./виток)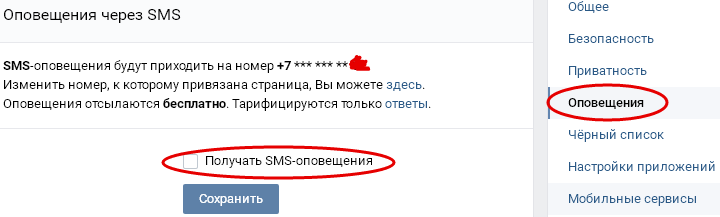
Идентификация различных форм ДНК  Положительная сверхспирализация хранит больше энергии, поэтому даже при более высоких температурах ДНК не денатурирует. Даже фермент не может распознать положительно суперскрученную ДНК и не может ее разрезать.
Положительная сверхспирализация хранит больше энергии, поэтому даже при более высоких температурах ДНК не денатурирует. Даже фермент не может распознать положительно суперскрученную ДНК и не может ее разрезать. Третья молекула ДНК накручена вокруг друг друга с некоторыми изгибами, а четвертая сверхскручена.
Третья молекула ДНК накручена вокруг друг друга с некоторыми изгибами, а четвертая сверхскручена.
Измерение топологии по динамике путем получения числа Черна из числа связи
 обращений
обращений Предметы
Abstract
 Распространяя соответствующее предложение на системы Флоке, мы измеряем число зацепления, которое характеризует траектории вихрей в импульсном пространстве, возникающих после сильного гашения. Заметим, что оно прямо соответствует числу Черна в основном состоянии. Это отношение один к одному между динамическим и статическим топологическими индексами позволяет нам экспериментально наметить фазовую диаграмму нашей системы. Кроме того, мы измеряем мгновенное число Черна и показываем, что оно остается равным нулю при унитарной динамике.
Распространяя соответствующее предложение на системы Флоке, мы измеряем число зацепления, которое характеризует траектории вихрей в импульсном пространстве, возникающих после сильного гашения. Заметим, что оно прямо соответствует числу Черна в основном состоянии. Это отношение один к одному между динамическим и статическим топологическими индексами позволяет нам экспериментально наметить фазовую диаграмму нашей системы. Кроме того, мы измеряем мгновенное число Черна и показываем, что оно остается равным нулю при унитарной динамике. Введение
 Вместо этого они характеризуются целочисленными топологическими индексами, которые топологически защищены и могут изменять значение только при закрытии разрыва. Важную роль играет число Черна, характеризующее топологию заполненных зон в двумерных решетчатых системах. Он фиксирует обмотку собственных состояний и определяется через интеграл кривизны Берри по первой зоне Бриллюэна. Лента с ненулевым числом Черна топологически нетривиальна. Когда самая высокая заполненная зона нетривиальна и полностью заполнена, состояние называется топологическим изолятором. Ненулевые числа Черна также лежат в основе целочисленного квантового эффекта Холла, возникающего в двумерных системах, подверженных сильному перпендикулярному магнитному полю, и отвечают за идеальное квантование холловской проводимости. По принципу объемно-граничного соответствия число Черна объемных зон также определяет количество киральных проводящих краевых состояний, которые лежат в запрещенной зоне и вызывают топологически защищенный транспорт.
Вместо этого они характеризуются целочисленными топологическими индексами, которые топологически защищены и могут изменять значение только при закрытии разрыва. Важную роль играет число Черна, характеризующее топологию заполненных зон в двумерных решетчатых системах. Он фиксирует обмотку собственных состояний и определяется через интеграл кривизны Берри по первой зоне Бриллюэна. Лента с ненулевым числом Черна топологически нетривиальна. Когда самая высокая заполненная зона нетривиальна и полностью заполнена, состояние называется топологическим изолятором. Ненулевые числа Черна также лежат в основе целочисленного квантового эффекта Холла, возникающего в двумерных системах, подверженных сильному перпендикулярному магнитному полю, и отвечают за идеальное квантование холловской проводимости. По принципу объемно-граничного соответствия число Черна объемных зон также определяет количество киральных проводящих краевых состояний, которые лежат в запрещенной зоне и вызывают топологически защищенный транспорт.
 Эта характеристика представляет собой прямое измерение чисел Черна в модели Холдейна. Аналогичный подход для спин-орбитально-связанной зонной структуры был недавно продемонстрирован в работе [3]. 17 . Наконец, используя томографию состояния эволюционирующей во времени волновой функции с временным разрешением, мы экспериментально показываем, что мгновенное число Черна действительно остается нулевым во время динамики.
Эта характеристика представляет собой прямое измерение чисел Черна в модели Холдейна. Аналогичный подход для спин-орбитально-связанной зонной структуры был недавно продемонстрирован в работе [3]. 17 . Наконец, используя томографию состояния эволюционирующей во времени волновой функции с временным разрешением, мы экспериментально показываем, что мгновенное число Черна действительно остается нулевым во время динамики. Результаты
Описание Флоке ведомой гексагональной решетки
 \dagger \шляпа a_l + \mathop {\sum}\limits_{l \in B} {\Delta _{AB}} \шляпа n_l$$
\dagger \шляпа a_l + \mathop {\sum}\limits_{l \in B} {\Delta _{AB}} \шляпа n_l$$ 2/\hbar \omega\). Заметим, что ширина нетривиальной области шире, чем в случае без начального смещения, поскольку эффективные элементы следующего за ближайшим соседнего туннеля больше (∝ α 0 , а не ∝ α 2 ) (см. Методы). Переходя от кругового сотрясения к общей фазе сотрясения ϕ между направлениями x и y , можно получить фазовую диаграмму, показанную на рис. 3, напоминающую диаграмму модели Холдейна 28 .
2/\hbar \omega\). Заметим, что ширина нетривиальной области шире, чем в случае без начального смещения, поскольку эффективные элементы следующего за ближайшим соседнего туннеля больше (∝ α 0 , а не ∝ α 2 ) (см. Методы). Переходя от кругового сотрясения к общей фазе сотрясения ϕ между направлениями x и y , можно получить фазовую диаграмму, показанную на рис. 3, напоминающую диаграмму модели Холдейна 28 . Дополнительный рисунок 1
Дополнительный рисунок 1 На самом деле в такой двухзонной системе число Черна имеет простую геометрическую интерпретацию: оно подсчитывает, сколько раз \(\widehat {\mathbf{h}}({\mathbf{k}})\) покрывает Сфера Блоха на 92k{\kern 1pt} \Omega ({\mathbf{k}})\) путем интегрирования по первой зоне Бриллюэна.
На самом деле в такой двухзонной системе число Черна имеет простую геометрическую интерпретацию: оно подсчитывает, сколько раз \(\widehat {\mathbf{h}}({\mathbf{k}})\) покрывает Сфера Блоха на 92k{\kern 1pt} \Omega ({\mathbf{k}})\) путем интегрирования по первой зоне Бриллюэна. Томография состояния с временным разрешением
 {\mathrm{i}}({\mathbf{k}})\) и следуя динамика. Когда блоховский вектор 9 эволюционировавшего во времени состояния1042 ψ ( k , t ) находится на одном из полюсов, это приводит к отсутствию динамики на томографии и к вихрю в азимутальном фазовом профиле. B Пример изображения плотности импульса N ( K ), полученная путем расширения по времени полета для размола Δ = −2 π ⋅ 372 Гц, эволюция T = 0,4297 MS и тома и тома и тома и тома и тома и тома и тома и тома и тома и тома и тома, и тома, и тома, и тома, и тома. время t ′ = 104 мкс. Шестиугольник отмечает первую зону Бриллюэна. с Интерференция подрешеток A и B отображает прецессию в колебание плотности, из которого получают фазу ϕ ( k , t ) и амплитуду sin ( θ ( k , t )) (ср. уравнение (7)). На графике показаны осцилляции с соответствующей подгонкой для выбранного пикселя изображения в b , т.
{\mathrm{i}}({\mathbf{k}})\) и следуя динамика. Когда блоховский вектор 9 эволюционировавшего во времени состояния1042 ψ ( k , t ) находится на одном из полюсов, это приводит к отсутствию динамики на томографии и к вихрю в азимутальном фазовом профиле. B Пример изображения плотности импульса N ( K ), полученная путем расширения по времени полета для размола Δ = −2 π ⋅ 372 Гц, эволюция T = 0,4297 MS и тома и тома и тома и тома и тома и тома и тома и тома и тома и тома и тома, и тома, и тома, и тома, и тома. время t ′ = 104 мкс. Шестиугольник отмечает первую зону Бриллюэна. с Интерференция подрешеток A и B отображает прецессию в колебание плотности, из которого получают фазу ϕ ( k , t ) и амплитуду sin ( θ ( k , t )) (ср. уравнение (7)). На графике показаны осцилляции с соответствующей подгонкой для выбранного пикселя изображения в b , т. е. в одном импульсном состоянии, и для времени эволюции t = 0,429 мс (синий) и t = 0,624 мс (красный) в системе Флоке. В то время как на иллюстрации для простоты предполагаются плоские полосы, где начальное состояние указывает на южный полюс, выводы о топологии остаются в силе для дисперсионных полос, использованных в эксперименте
е. в одном импульсном состоянии, и для времени эволюции t = 0,429 мс (синий) и t = 0,624 мс (красный) в системе Флоке. В то время как на иллюстрации для простоты предполагаются плоские полосы, где начальное состояние указывает на южный полюс, выводы о топологии остаются в силе для дисперсионных полос, использованных в эксперименте
Полноразмерное изображение
прецессия под действием томографического гамильтониана, которую можно наблюдать в времяпролетных измерениях. Для государства | ψ ( к )〉 = cos( θ ( k )/2)| A , k 〉 + sin( θ ( k )/2) e iϕ ( k ) | B , k 〉, соответствующий вектору Блоха
$${\mathbf{\psi}}({\mathbf{k}}) = \left({\begin{array}{*{20}{ c}} {{\ mathrm {sin}} (\ theta ({\ mathbf {k}}}} {\ mathrm {cos}} (\ phi ({\ mathbf {k}}))} \\ {{\ mathrm {sin}} (\ theta ({\ mathbf {k}}}} {\ mathrm {sin}} (\ phi ({\ mathbf {k}}))} \\ {{\ mathrm {cos}} ( \theta ({\mathbf{k}}))} \end{массив}} \right),$$ 92} \hfill \\ {} \hfill & = \hfill & {f ({\mathbf{k}})\{ 1 + {\mathrm{sin}}(\theta ({\mathbf{k}})) {\mathrm{cos}}(\phi ({\mathbf{k}}))\} ,} \hfill \end{array}$$
(6)
где (| A , k 〉, | B , k 〉) — полюса сферы Блоха, а f ( k ) — преобразование Фурье функции Ванье. Это измерение есть не что иное, как проекция на ось x сферы Блоха, | х , k 〉 = (| A , k 〉 + | B , k 〉)/2, в чем легко убедиться, сравнив x -компоненту блоховского вектора второе выражение для плотности импульса n ( k ).
Это измерение есть не что иное, как проекция на ось x сферы Блоха, | х , k 〉 = (| A , k 〉 + | B , k 〉)/2, в чем легко убедиться, сравнив x -компоненту блоховского вектора второе выражение для плотности импульса n ( k ).
Во всех экспериментах, описанных в рукописи, мы начинаем с заполненной нижней полосы | ψ i ( k )〉 исходного гамильтониана, описывающего голую решетку, и утонуть в окончательный гамильтониан, описывающий расшатанную решетку, т.е. между двумя «магнитными полями» ч i ( к ) и ч ф ( к ). После переменного времени эволюции t проведем томографию состояния в базисе исходной решетки закалкой к гамильтониану томографии позволяя системе развиваться в течение времени t ′. Закаленное состояние прецессирует около ч t ( к ) с частотой Δ AB определяется шириной запрещенной зоны томографического гамильтониана. Эта динамика порождает колебательный сигнал для импульсного распределения
Эта динамика порождает колебательный сигнал для импульсного распределения
$$\begin{array}{*{20}{l}} {n({\mathbf{k}},t\prime ) = f({\ mathbf {k}}) \ { 1 + {\ mathrm {sin}} (\ theta ({\ mathbf {k}}}} {\ mathrm {cos}} ({\ mathrm {\ Delta}} _ {AB} t\prime + \phi ({\mathbf{k}}))\} ,} \hfill \end{array}$$
(7)
, из которых θ ( k ) и ϕ ( k ) можно извлечь (см. рис. 4c).
Оригинальная томографическая схема 8,16,29 и предложение по увязке номер реф. 15 предположим, что гамильтониан томографии h t ( k ) является диагональным в подрешетке-базисе, т.е. соответствует полностью развязанным A и B подрешеткам и с плоскими дисперсионными соотношениями. В этом случае можно напрямую измерить углы θ ( k ) и ϕ ( k ), определенные выше, и можно напрямую получить кривизну Берри самой нижней полосы по уравнению. (4).
Томография состояния с полосами дисперсии
Здесь мы распространяем это понятие на томографию состояния в полосах дисперсии, т. 2/\hbar \omega \simeq h \cdot 500\,{\mathrm{Hz}}\), см. выше) , к которому легче получить доступ экспериментально даже при наличии внешней ловушки. В качестве основного результата мы находим, что топологические свойства могут быть точно получены из томографии в дисперсионных полосах, пока базис томографии сам по себе топологически тривиален, что всегда обеспечивается при использовании статической оптической решетки для томографии. Это также демонстрирует топологическую устойчивость нашей системы к искажениям. Отметим, что измерение в диагональном базисе, т.е. соответствующем полностью плоским зонам, возможно посредством разделения Штерна-Герлаха при использовании внутренних атомных уровней в качестве спина вместо псевдоспина подрешетки для генерации топологических структур 17,30 .
2/\hbar \omega \simeq h \cdot 500\,{\mathrm{Hz}}\), см. выше) , к которому легче получить доступ экспериментально даже при наличии внешней ловушки. В качестве основного результата мы находим, что топологические свойства могут быть точно получены из томографии в дисперсионных полосах, пока базис томографии сам по себе топологически тривиален, что всегда обеспечивается при использовании статической оптической решетки для томографии. Это также демонстрирует топологическую устойчивость нашей системы к искажениям. Отметим, что измерение в диагональном базисе, т.е. соответствующем полностью плоским зонам, возможно посредством разделения Штерна-Герлаха при использовании внутренних атомных уровней в качестве спина вместо псевдоспина подрешетки для генерации топологических структур 17,30 .
В то время как фазовый профиль, в целом, искажен для томографии в неплоских полосах, мы покажем здесь, что топологическая информация, закодированная в вихревых траекториях, не изменяется. {\mathrm{t}}({\mathbf{k}})\) так, чтобы он указывал на северный полюс для каждых 9{\mathrm{t}}({\mathbf{k}})\) (эффективный северный полюс) и вызывает динамический вихрь в томографии.
{\mathrm{t}}({\mathbf{k}})\) так, чтобы он указывал на северный полюс для каждых 9{\mathrm{t}}({\mathbf{k}})\) (эффективный северный полюс) и вызывает динамический вихрь в томографии.
Число Черна из томографии в дисперсионных полосах
Томография состояния в дисперсионных, но топологически тривиальных полосах также дает доступ к числу Черна. Это соответствует реконструкции состояния в базисе, который сам является недиагональным в подрешеточном базисе и имеет конечную кривизну Берри. Поэтому отношение измеренных углов θ ( k ) и ϕ ( k ) к кривизне Берри является более сложным и в принципе требует знания дисперсионных полос, т. Е. Матрицы вращения \ (\ шляпа R \). Вместо этого мы вводим искаженную кривизну Берри, вставляя θ ( k ) и ϕ ( k ) непосредственно в уравнение. (4). Интеграл искаженной кривизны Берри по полной зоне Бриллюэна квантуется, как и интеграл по реальной кривизне Берри, и равен числу Черна. Это так, потому что матрица вращения \(\шляпа R\), количественно определяющая искажение из-за h t ( k ) не создает монополи, пока базис томографии топологически тривиален. Точнее, квантование числа Черна выполняется для любой текстуры псевдоспина и вращение не меняет топологию, которая по-прежнему определяется направлением псевдоспина в точках Дирака, где матрица вращения тождественна. Это точное измерение топологических свойств даже в основе дисперсионных полос подчеркивает универсальность подхода томографии состояния.
Это так, потому что матрица вращения \(\шляпа R\), количественно определяющая искажение из-за h t ( k ) не создает монополи, пока базис томографии топологически тривиален. Точнее, квантование числа Черна выполняется для любой текстуры псевдоспина и вращение не меняет топологию, которая по-прежнему определяется направлением псевдоспина в точках Дирака, где матрица вращения тождественна. Это точное измерение топологических свойств даже в основе дисперсионных полос подчеркивает универсальность подхода томографии состояния.
Измерение мгновенного числа Черна
В качестве основного результата мы измеряем мгновенное число Черна эволюционировавшего во времени состояния после закалки в нетривиальный гамильтониан. Мы получаем мгновенную искаженную кривизну Берри из томографии состояния с временным разрешением в дисперсионных полосах, показанных на рис. 5. Мы обнаруживаем, что после закалки состояние развивает сильную кривизну Берри с все более тонкой структурой, но извлеченное число Черна остается очень близким к нулю с | С | < 0,02.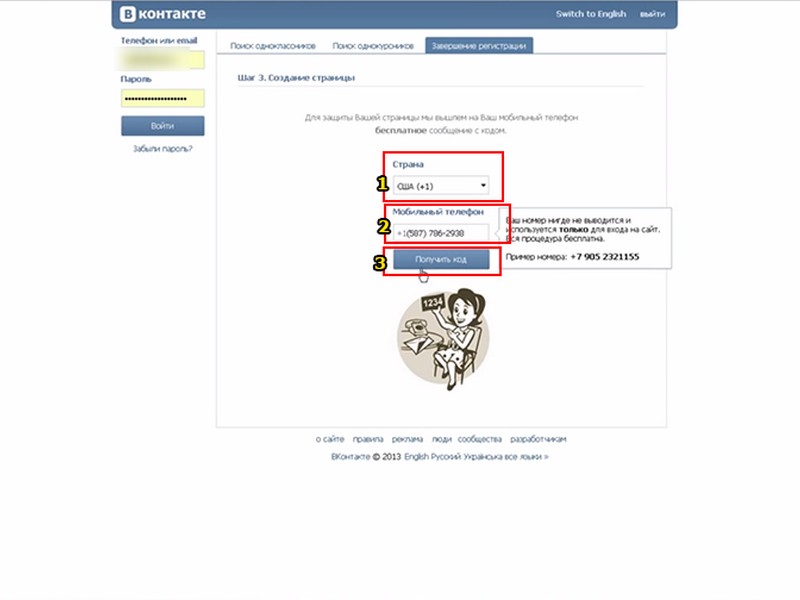 Это подтверждает вывод о том, что число Черна, которое диктуется тривиальным гамильтонианом до закалки, не может измениться при унитарной динамике 32,33,34,35 . Недавно было высказано предположение, что, наоборот, инвариант Черна–Саймонса в одномерных системах может изменяться в процессе динамики 36 .
Это подтверждает вывод о том, что число Черна, которое диктуется тривиальным гамильтонианом до закалки, не может измениться при унитарной динамике 32,33,34,35 . Недавно было высказано предположение, что, наоборот, инвариант Черна–Саймонса в одномерных системах может изменяться в процессе динамики 36 .
Мгновенная кривизна Берри и мгновенное число Черна. Данные томографии состояния с временным разрешением в дисперсионных полосах, показывающие азимутальную фазу ? Из этих данных получаем мгновенную искаженную кривизну Берри ( c ) и мгновенное число Черна эволюционировавшего во времени состояния в единицах обратного квадрата длины вектора обратной решетки b . Время эволюции составляет 156, 273, 390, 507 и 663 мкс, а числа Черна равны -0,001, -0,008, -0,013, -0,016, -0,015. Хотя искаженная кривизна Берри развивает более тонкие структуры в зависимости от времени, мгновенное число Черна остается равным нулю, что обусловлено унитарной эволюцией. Штриховыми линиями разделены регионы, где государство расположено в южном и северном полушарии (зарисовки)
Штриховыми линиями разделены регионы, где государство расположено в южном и северном полушарии (зарисовки)
Полноразмерное изображение
Схема томографии не может различать северное и южное полушария сферы Блоха, потому что она дает доступ к sin ( θ ( k )) вместо самого θ ( k ) . Это в принципе может быть дополнено измерениями картирования адиабатических полос 29 . В качестве альтернативы можно определить импульсы, когда состояние указывает на экватор и меняется между двумя полушариями, и соответствующим образом скорректировать знак кривизны Берри 29 . На рис. 5 мы идентифицируем эти импульсы и помечаем их пунктирными линиями. Эти импульсы идентифицируются по локальному максимуму sin ( θ ( k )), хотя из-за затухания в системе, возникающего при нагреве Флоке, sin ( θ ( k )) не достигает единицы . В данных искаженной кривизны Берри видно, что кривизна сокращается до нуля отдельно для каждой области, разделенной пунктирными линиями. Поэтому коррекция знака не требуется.
Поэтому коррекция знака не требуется.
Наблюдение за динамическими вихрями
В то время как развивающееся во времени состояние имеет мгновенное число Черна, равное нулю, независимое от числа Черна основного гамильтониана постгашения, его динамика содержит информацию о топологии последнего через вихревую структуру фазовый профиль.
Поэтому в оставшейся части рукописи мы сосредоточимся на завихренности фазовых профилей томографии состояния с временным разрешением (см. рис. 6). Мы вычисляем завихренность как v ( k ) = ∇ k × ∇ k ϕ ( k ) 9096 Из этого анализа мы четко идентифицируем статические вихри в точках Γ и K ′ или K и динамические вихри, которые появляются и исчезают парами и очерчивают замкнутый контур 16 (см. рис. 6c).
Рис. 6 Извлечение завихренности фазовых профилей. a Азимутальный фазовый профиль ϕ ( k ) развитого во времени состояния с идентифицированными вихрями, отмеченными красными и синими кружками в качестве ориентира для глаза. b Завихренность фазовых профилей с положением вихрей и антивихрей, отмеченных синими и красными квадратами соответственно. В то время как сам фазовый профиль искажен для томографии состояния в дисперсионных полосах, вихри могут быть четко идентифицированы, и их интерпретация не подвергается риску. с На интегрированной по времени завихренности отчетливо видны статические вихри в точках Γ и K ′ и замкнутый контур динамических вихрей. Расстройка δ = −2 π ⋅ 372 Гц; Время эволюции составляет T 1 = 0,507 мс, T 2 = 0,663 мс и T 3 = 0,819 мс
b Завихренность фазовых профилей с положением вихрей и антивихрей, отмеченных синими и красными квадратами соответственно. В то время как сам фазовый профиль искажен для томографии состояния в дисперсионных полосах, вихри могут быть четко идентифицированы, и их интерпретация не подвергается риску. с На интегрированной по времени завихренности отчетливо видны статические вихри в точках Γ и K ′ и замкнутый контур динамических вихрей. Расстройка δ = −2 π ⋅ 372 Гц; Время эволюции составляет T 1 = 0,507 мс, T 2 = 0,663 мс и T 3 = 0,819 мс
Полноразмерное изображение
MAPPAP далее мы покажем, что число Черна лежащего в основе гамильтониана отображается в связующее число этих динамических вихрей, которое учитывает, охватывает ли этот контур один из статических вихрей или нет
15 . Основная идея состоит в том, что число Черна соответствует обертке сферы Блоха, которую можно измерить, наблюдая, содержит ли \(\widehat {\mathbf{h}}({\mathbf{k}})\) оба полюса, а плавно охватывающий экватор (см. {\mathrm{f}}({\mathbf{k}})\) является гладким , непрерывный и дисперсионный, т.е. плавно распространяется по сфере Блоха 9{\ mathrm {f}} ({\ mathbf {k}}) \) указывает на экватор. Топологически нетривиальный гамильтониан, содержащий оба полюса, требует, чтобы этот контур окружал статический вихрь, так что его нужно было пересечь один раз (или нечетное количество раз) между двумя статическими вихрями. Поэтому отсутствие динамического вихревого контура можно отождествить с нулевым числом Черна. Важно отметить, что о топологии свидетельствует не простое существование контура, а его топологический индекс: явно возможны тривиальные контуры, которые не охватывают статический вихрь. Рис. 7
{\mathrm{f}}({\mathbf{k}})\) является гладким , непрерывный и дисперсионный, т.е. плавно распространяется по сфере Блоха 9{\ mathrm {f}} ({\ mathbf {k}}) \) указывает на экватор. Топологически нетривиальный гамильтониан, содержащий оба полюса, требует, чтобы этот контур окружал статический вихрь, так что его нужно было пересечь один раз (или нечетное количество раз) между двумя статическими вихрями. Поэтому отсутствие динамического вихревого контура можно отождествить с нулевым числом Черна. Важно отметить, что о топологии свидетельствует не простое существование контура, а его топологический индекс: явно возможны тривиальные контуры, которые не охватывают статический вихрь. Рис. 7 Иллюстрация сопоставления числа связи и числа Черна. a Прообразы полюсов на сфере Блоха образуют контуры в зоне Бриллюэна. В точках Дирака, где гамильтониан указывает на один из полюсов, динамики нет, и состояние останется на южном полюсе и создаст статический вихрь (зеленые и оранжевые точки).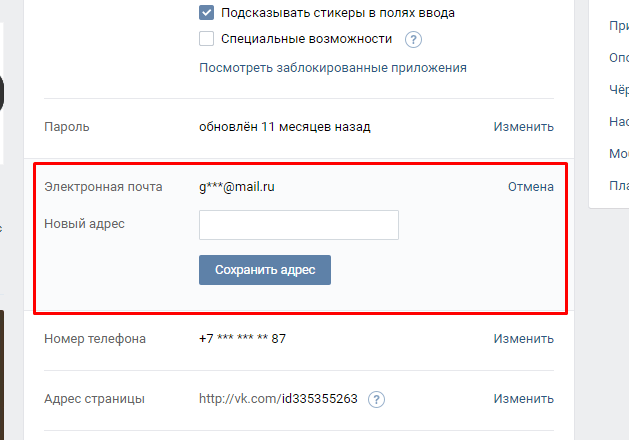 Там, где гамильтониан лежит на экваторе, эволюционировавшее во времени состояние динамически достигнет северного полюса и создаст динамический вихрь. Эти динамические вихри движутся по контуру, который является прообразом экватора сферы Блоха (серая линия). Число Черна гамильтониана можно вывести из числа зацепления контура: если контур динамического вихря охватывает один из статических вихрей, то оба статических вихря соответствуют противоположным полюсам, так что гамильтониан топологически нетривиален. Это можно увидеть, проследив динамику вдоль пути, соединяющего две точки Дирака (пунктирная линия). В изображенном случае число Черна равно 1,9.1072 b То же, что и ( a ), но для случая числа Черна 0
Там, где гамильтониан лежит на экваторе, эволюционировавшее во времени состояние динамически достигнет северного полюса и создаст динамический вихрь. Эти динамические вихри движутся по контуру, который является прообразом экватора сферы Блоха (серая линия). Число Черна гамильтониана можно вывести из числа зацепления контура: если контур динамического вихря охватывает один из статических вихрей, то оба статических вихря соответствуют противоположным полюсам, так что гамильтониан топологически нетривиален. Это можно увидеть, проследив динамику вдоль пути, соединяющего две точки Дирака (пунктирная линия). В изображенном случае число Черна равно 1,9.1072 b То же, что и ( a ), но для случая числа Черна 0
Полноразмерное изображение
Обратите внимание, что аргумент можно сформулировать в более общем виде, рассматривая прообразы любых двух ортогональных векторов на сфера Блоха 15 . Затем число Черна отображается на связующее число двух траекторий в пространстве, охватываемом k x , k y и временем (сравните рис.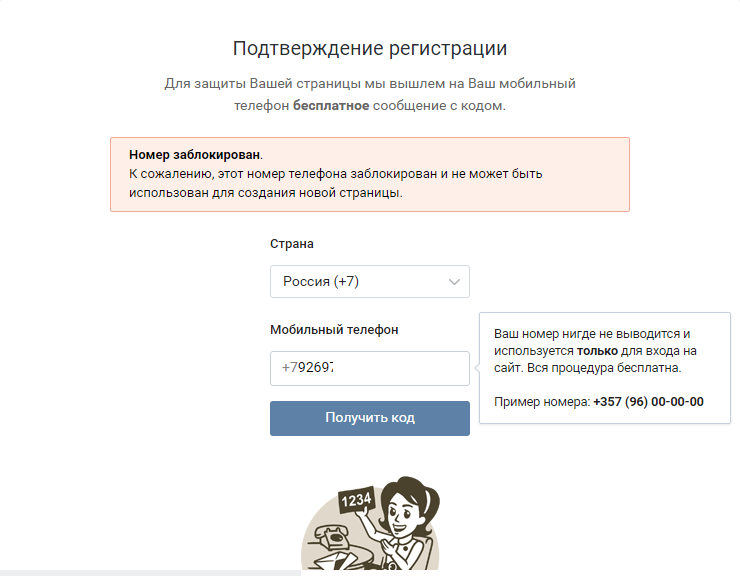 1), и может быть связано с числом Хопфа. инвариант. Такое число зацеплений, характеризующее изолятор Хопфа, недавно наблюдалось при квантовом моделировании с использованием вакансионного центра азота 37 . Эта более общая картина двух контуров в трехмерном пространстве, которые могут быть связаны, является причиной термина связующее число, которое мы также используем здесь, когда рассматриваем проекцию на у самолет.
1), и может быть связано с числом Хопфа. инвариант. Такое число зацеплений, характеризующее изолятор Хопфа, недавно наблюдалось при квантовом моделировании с использованием вакансионного центра азота 37 . Эта более общая картина двух контуров в трехмерном пространстве, которые могут быть связаны, является причиной термина связующее число, которое мы также используем здесь, когда рассматриваем проекцию на у самолет.
Аргументы можно распространить и на большие числа Черна | С | > 1. Эта ситуация будет соответствовать либо нескольким парам статических вихрей, которые (отдельно или совместно) окружены динамическим вихревым контуром, либо многозарядным статическим вихрям (определяемым несколькими фазными обмотками), окруженным динамическим вихревым контуром. Большие числа Черна | С | > 1 может, например, появляться для сильных скачкообразных членов от третьего соседа в модели Холдейна N3, что приводит к дополнительным точкам спутника Дирака 38,39,40 . В управляемых гексагональных решетках это может произойти, когда туннелирование следующего соседа перенормировано близко к нулю 41 .
В управляемых гексагональных решетках это может произойти, когда туннелирование следующего соседа перенормировано близко к нулю 41 .
Измерение топологической фазовой диаграммы
В качестве основного результата мы используем связь между числом зацепления и числом Черна для экспериментального определения топологического фазового перехода эффективного гамильтониана. На рис. 8а показаны данные интегральной по времени завихренности для разных закалок в области Черна 0 и Черна 1 фазовой диаграммы (различные расстройки встряхивания решетки). В то время как статические вихри на Γ и 9На всех наборах данных видны 1042 K ′ точек, в наборах данных отчетливо выделяются дополнительные вихревые контуры для околорезонансного встряхивания. Мы легко подсчитываем число зацеплений этих контуров и тем самым получаем число Черна конечного гамильтониана. С учетом расстройки δ получаем фазовую диаграмму, показанную на рис. 8б. На нем имеется топологически нетривиальная область с числом Черна 1 для конечного интервала отстроек (соответствующего малым значениям ∆ эфф ), окруженный топологически тривиальными областями. Измеренное число Черна хорошо согласуется с теоретическим предсказанием, полученным в результате численного моделирования (см. Методы). Хотя фазовые данные становятся более зашумленными при длительном времени эволюции, что может привести к дополнительным фиктивным вихрям при оценке данных, это не вызывает проблемы, поскольку они не описывают замкнутые контуры вокруг статических вихрей и, следовательно, не будут вносить вклад в число связей. Эта топологическая величина защищена от шума. Однако вихри на рис. 8а (iii) при больших временах эволюции (светлый оттенок) в основном обусловлены не шумом, а когерентной динамикой, которая позволяет появляться дополнительным вихрям.
Измеренное число Черна хорошо согласуется с теоретическим предсказанием, полученным в результате численного моделирования (см. Методы). Хотя фазовые данные становятся более зашумленными при длительном времени эволюции, что может привести к дополнительным фиктивным вихрям при оценке данных, это не вызывает проблемы, поскольку они не описывают замкнутые контуры вокруг статических вихрей и, следовательно, не будут вносить вклад в число связей. Эта топологическая величина защищена от шума. Однако вихри на рис. 8а (iii) при больших временах эволюции (светлый оттенок) в основном обусловлены не шумом, а когерентной динамикой, которая позволяет появляться дополнительным вихрям.
Составление топологической фазовой диаграммы с использованием номера связи. a Исходные данные наблюдаемых вихрей, суммированные по всем временным шагам (красная точка: положительная киральность, синяя точка: отрицательная киральность; оттенок указывает временной шаг, на котором присутствовал вихрь).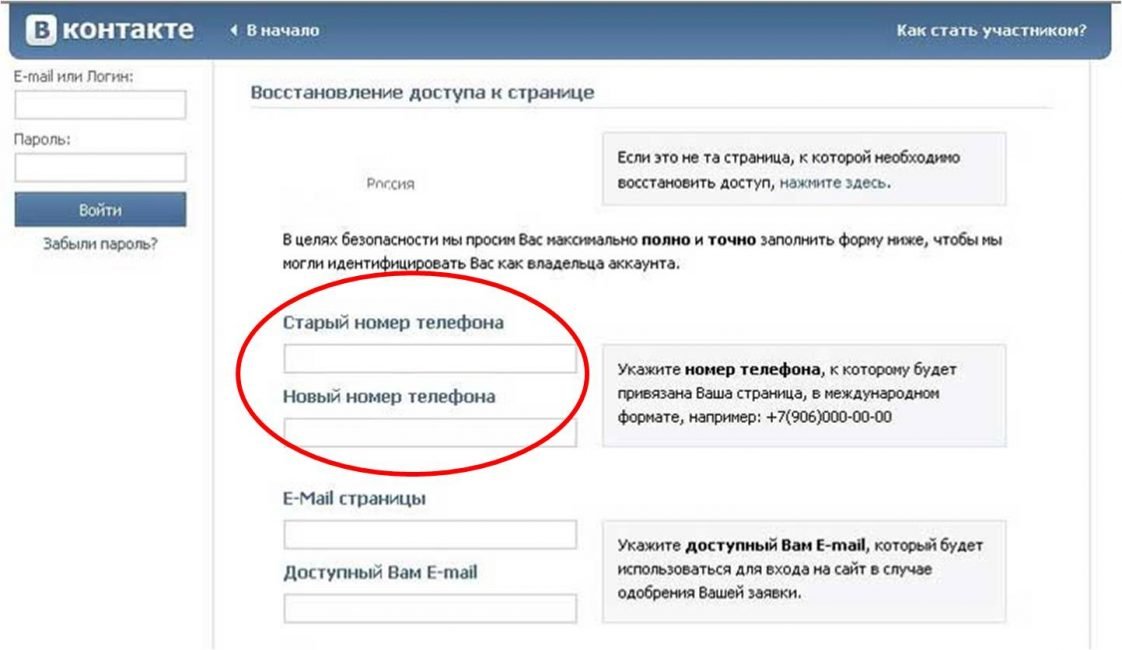 Шестиугольник отмечает первую зону Бриллюэна. Контуры динамического вихря выделены ориентиром для глаз (серая линия). b Число Черна получается из числа связи этих динамических вихревых контуров (или отсутствия контура) и строится для различных расстроек тряски (перерез фазовой диаграммы, соответствующий серой линии на рис. 3). Область с нетривиальным числом Черна хорошо согласуется с предсказанием полного численного расчета (сплошная линия). c Расчетные полосы Флоке для различных расстроек, иллюстрирующие замыкание точек Дирака при топологических фазовых переходах
Шестиугольник отмечает первую зону Бриллюэна. Контуры динамического вихря выделены ориентиром для глаз (серая линия). b Число Черна получается из числа связи этих динамических вихревых контуров (или отсутствия контура) и строится для различных расстроек тряски (перерез фазовой диаграммы, соответствующий серой линии на рис. 3). Область с нетривиальным числом Черна хорошо согласуется с предсказанием полного численного расчета (сплошная линия). c Расчетные полосы Флоке для различных расстроек, иллюстрирующие замыкание точек Дирака при топологических фазовых переходах
Изображение в натуральную величину
Извлечение знака числа Черна хиральность наблюдаемых вихрей и направление их движения (см. рис. 9) (сравните ссылку
15 ). Мы можем определить киральность х d контура динамического вихря по направлению движения динамических вихрей положительной киральности. Тогда знак связующего числа может быть определен как произведение — х d х с , где х с обозначает хиральность замкнутого статического вихря. Из этого знака непосредственно получается знак числа Черна нижней блоховской полосы (см. Методы). На рисунке 9 показаны данные о вихрях с временным разрешением для двух разных направлений сотрясения круговой решетки, что приводит к числам Черна противоположного знака. В то время как хиральность контура вихря в обоих случаях одинакова, хиральность замкнутого вихря изменяется в зависимости от направления движения, что прямо указывает на противоположный знак числа Черна. Рис. 9
Из этого знака непосредственно получается знак числа Черна нижней блоховской полосы (см. Методы). На рисунке 9 показаны данные о вихрях с временным разрешением для двух разных направлений сотрясения круговой решетки, что приводит к числам Черна противоположного знака. В то время как хиральность контура вихря в обоих случаях одинакова, хиральность замкнутого вихря изменяется в зависимости от направления движения, что прямо указывает на противоположный знак числа Черна. Рис. 9 Знак номера привязки. a Вихревые данные в нетривиальном режиме (фаза встряхивания π /2 и расстройка встряхивания δ /2 π = −372 Гц). На первом подрисунке показаны интегрированные по времени данные, а на других подрисунках показаны последовательные стробоскопические шаги по времени t 3 = 21⋅ T /4 после закалки, где T — период вождения. Стрелками отмечено направление движения соответствующих вихрей.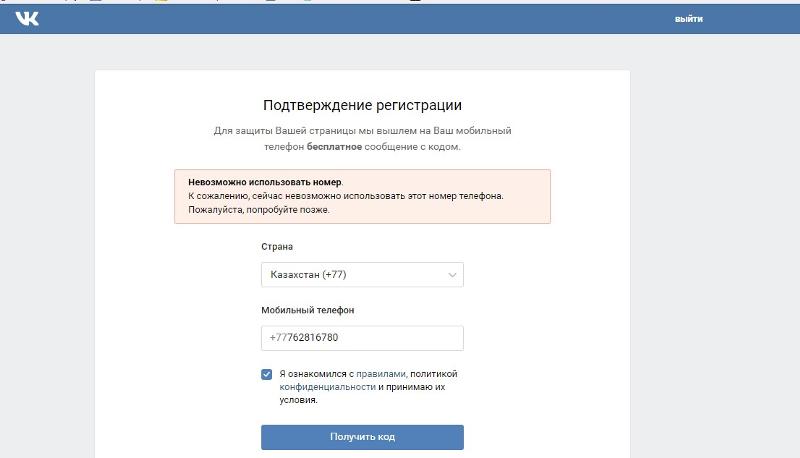 Контур вихря имеет положительную киральность, в то время как замкнутый статический вихрь имеет отрицательную киральность, показывая число Черна +1 (см. текст). B , обратное встряхивание (серая точка на рис. 3) для Δ /2 π = −359 Гц и для временных шагов T 1 = 14– T /4, T 9988 T /4, T 8 2 = 18⋅ Т /4, т 3 = 22⋅ T /4 после закалки. Хиральность замкнутого вихря теперь инвертирована, и число Черна равно −1
Контур вихря имеет положительную киральность, в то время как замкнутый статический вихрь имеет отрицательную киральность, показывая число Черна +1 (см. текст). B , обратное встряхивание (серая точка на рис. 3) для Δ /2 π = −359 Гц и для временных шагов T 1 = 14– T /4, T 9988 T /4, T 8 2 = 18⋅ Т /4, т 3 = 22⋅ T /4 после закалки. Хиральность замкнутого вихря теперь инвертирована, и число Черна равно −1
Полноразмерное изображение
Измерение микродвижения
Чтобы получить лучшее разрешение динамики вихря, мы измеряем динамику с шагом в четверть периода возбуждения T = 2 π / ω = 156 мкс. Таким образом, мы пробуем микродвижение системы Флоке 22,23,24,42 . Поскольку микродвижение положений вихрей в нашем случае мало по сравнению с контурами их траекторий (см. Методы), оно не влияет на измерение числа Черна.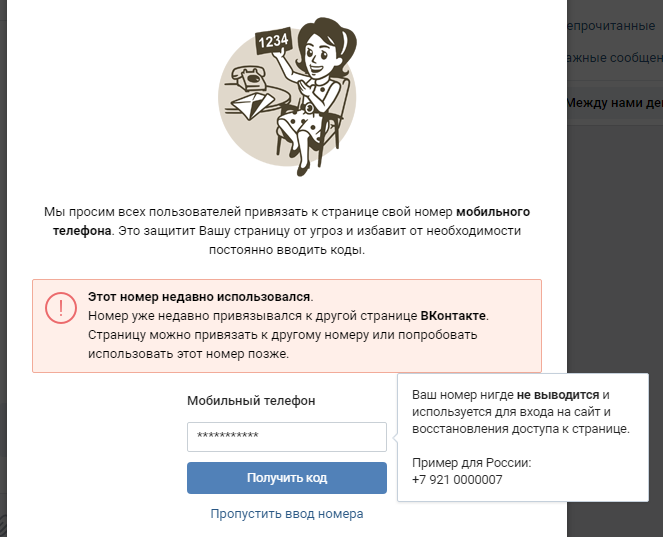
На рис. 10 мы оцениваем микродвижение статических точек Дирака в экспериментальных данных. Мы находим приблизительно круговое движение с движущей частотой или кратной ей, как предсказано выводом, представленным в Методах. Как и ожидалось от масштабирования микродвижения с \(J_{AB}/(\hbar \omega)\), которое порядка ~0,1, амплитуда микродвижения очень мала (несколько процентов длины вектора решетки | b |) и не влияет на измерение топологии системы.
Рис. 10 Микродвижение статических точек Дирака. Положение статических вихрей для наблюдаемых временных шагов (кратные 39 μ с, период движения T равен четырем временным шагам). a Статический вихрь в точке Γ. b Статический вихрь в одной из точек K ′. Позиция k x смещена на + 0,2 | б | в в и +0,7| б | в b для лучшей видимости. Движение примерно круговое с k x направление (синие точки) не совпадает по фазе с направлением k y (оранжевые точки).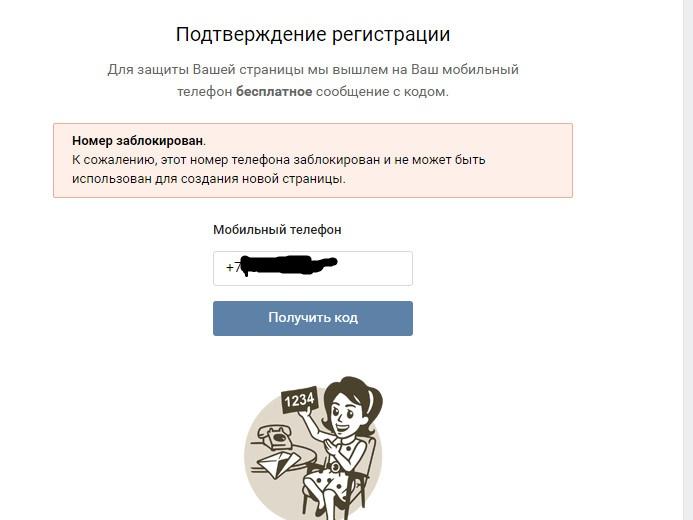 Вихрь в точке Γ движется преимущественно с задающей частотой. Вихрь в точке K движется преимущественно с удвоенной частотой возбуждения. Линии показывают приближения в качестве ориентира для глаза с фиксированными периодами T и T /2 соответственно. Обе амплитуды очень малы (несколько процентов от длины вектора решетки | б |). Позиции определяются с точностью до одного пикселя изображения, что соответствует 0,018| б |. Отстройка δ /2 π = −478 Гц
Вихрь в точке Γ движется преимущественно с задающей частотой. Вихрь в точке K движется преимущественно с удвоенной частотой возбуждения. Линии показывают приближения в качестве ориентира для глаза с фиксированными периодами T и T /2 соответственно. Обе амплитуды очень малы (несколько процентов от длины вектора решетки | б |). Позиции определяются с точностью до одного пикселя изображения, что соответствует 0,018| б |. Отстройка δ /2 π = −478 Гц
Обсуждение
Таким образом, мы нашли экспериментальные доказательства того, что число Черна, которое характеризует топологически нетривиальные свойства изолирующих равновесных состояний квантовой системы, определяет и свойства ее динамики вдали от равновесия. А именно, мы заметили, что оно прямо соответствует числу зацеплений траекторий k — космические вихри, возникающие после сильного остывания. Кроме того, мы измерили мгновенное число Черна эволюционировавшего во времени состояния и обнаружили, что оно действительно остается равным нулю при унитарной динамике. Мы также определили знак числа зацепления по хиральности вихрей и направлению их движения. Мы показываем, что томография состояния дает правильные топологические свойства также для измерений в дисперсионных полосах, что позволяет использовать более широкие нетривиальные области.
Мы также определили знак числа зацепления по хиральности вихрей и направлению их движения. Мы показываем, что томография состояния дает правильные топологические свойства также для измерений в дисперсионных полосах, что позволяет использовать более широкие нетривиальные области.
Интересен вопрос, насколько такое соответствие между топологическими свойствами в равновесии и вдали от равновесия можно обобщить на другие топологические показатели, такие, например, как число витков W3, характеризующее топологические фазы Флоке 43,44 , к многодиапазонным системам 45 или к сильно взаимодействующим системам. Наши эксперименты представляют собой прямое измерение и визуализацию топологического индекса в отличие от обычного подхода к выводу топологии из квантования отклика, например, проводимости Холла 13 или кругового дихроизма 14 .
Методы
Подготовка системы
Эксперименты начинаются с ультрахолодного облака размером около 3 × 10 5 спин-поляризованного 40 Атомы К в состоянии F = 9/2, m F = 9/2. Мы линейно увеличиваем гексагональную оптическую решетку за 10 мс и удерживаем еще 5 мс, прежде чем включить встряхивание решетки. В направлении, ортогональном гексагональной решетке, образец гармонически ограничен, т.е. реализует решетку из трубок. Решетка образована интерференцией трех лазерных лучей с длиной волны λ L = 1064 нм, и мы вводим AB — смещение за счет контроля поляризации лучей 8 . Мы отображаем образец на ПЗС-камере после 21 мс времяпролетного расширения, что приводит к увеличению, где длина вектора решетки | б | соответствует 56 пикселям. Томография состояния использует 32 временных шага по 8 мкс с и синусоидальную аппроксимацию, включая экспоненциальное затухание (см. рис. 4).
Мы линейно увеличиваем гексагональную оптическую решетку за 10 мс и удерживаем еще 5 мс, прежде чем включить встряхивание решетки. В направлении, ортогональном гексагональной решетке, образец гармонически ограничен, т.е. реализует решетку из трубок. Решетка образована интерференцией трех лазерных лучей с длиной волны λ L = 1064 нм, и мы вводим AB — смещение за счет контроля поляризации лучей 8 . Мы отображаем образец на ПЗС-камере после 21 мс времяпролетного расширения, что приводит к увеличению, где длина вектора решетки | б | соответствует 56 пикселям. Томография состояния использует 32 временных шага по 8 мкс с и синусоидальную аппроксимацию, включая экспоненциальное затухание (см. рис. 4).
Точное чис-° вне плоскости решетки, с относительной фазой плоскостной и внеплоскостной поляризации 0, 2
π /3 и 4 π /3 для трех лучей). Мы рассчитали точную зонную структуру для этой геометрии и различной глубины решетки V 0 .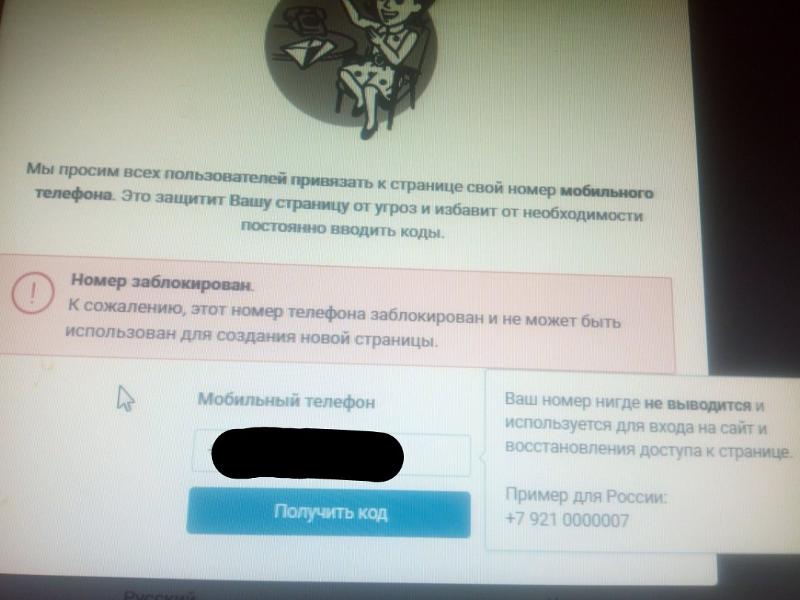 Чтобы определить точное значение глубины решетки, мы используем данные о расстоянии между полосами голой решетки из томографии состояния и подгоняем к ней точную структуру полос (см. Дополнительный рисунок 1 и Дополнительное примечание 1). Таким образом мы компенсируем небольшие дрейфы глубины решетки. Затем мы подгоняем модель сильной связи к точной зонной структуре и получаем Δ AB , J AB , J AA и J BB . Значения J AA / h находятся в диапазоне 80–115 Гц, а J BB / h — в диапазоне от −6 Гц до 6 Гц. Для сравнения с эффективным гамильтонианом малые J AA и J BB игнорируются.
Чтобы определить точное значение глубины решетки, мы используем данные о расстоянии между полосами голой решетки из томографии состояния и подгоняем к ней точную структуру полос (см. Дополнительный рисунок 1 и Дополнительное примечание 1). Таким образом мы компенсируем небольшие дрейфы глубины решетки. Затем мы подгоняем модель сильной связи к точной зонной структуре и получаем Δ AB , J AB , J AA и J BB . Значения J AA / h находятся в диапазоне 80–115 Гц, а J BB / h — в диапазоне от −6 Гц до 6 Гц. Для сравнения с эффективным гамильтонианом малые J AA и J BB игнорируются. Мы сравниваем наши данные с точными числами управляемой модели сильной связи (рис. 3 и 8). В этом расчете оператор временной эволюции \(\hat U(t,0)\) вычисляется с помощью квантования времени как произведение операторов временной эволюции для постоянных гамильтонианов (сравните ссылку 8 ).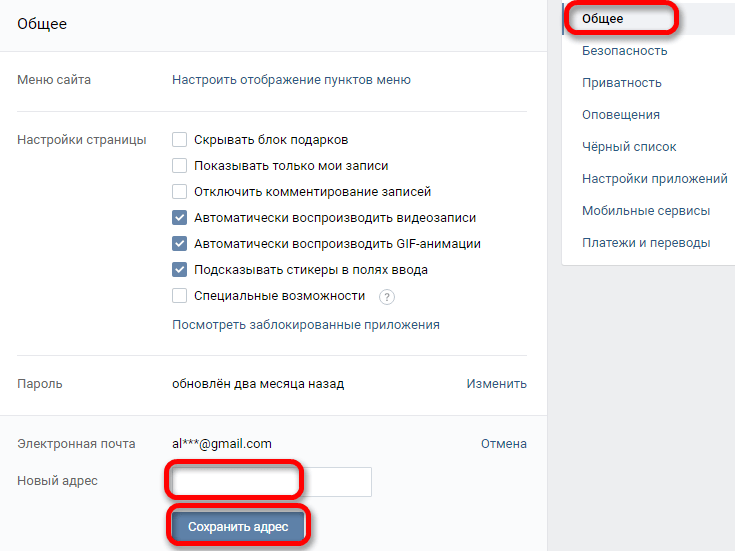 Этот метод работает для любого времени эволюции t , включая субстробоскопические временные шаги, где автоматически учитывается микродвижение. Это зависит от начальной фазы встряхивания, которую мы установили равной нулю, как и в эксперименте. Чтобы получить прогноз для контуров динамического вихря, мы вычисляем перекрытие эволюционировавшего во времени состояния \(|\psi (t)\rangle = \hat U(t,0)|\psi (0)\rangle\) с исходное состояние | ψ (0)〉 и считать импульсы, где это перекрытие ниже порога 0,02. Эта процедура находит импульсы, при которых ожидаются динамические вихри с учетом неплоскостности полос, а конечный порог обусловлен численной реализацией. В последнем столбце дополнительного рисунка 1 эти числовые данные суммируются для всех временных шагов (с использованием разрешения в восемь временных шагов за период управления, чтобы лучше разрешить контуры). Фазовые диаграммы на рис. 3 и 8 получаются из этих точных чисел, а число Черна вычисляется как интеграл кривизны Берри.
Этот метод работает для любого времени эволюции t , включая субстробоскопические временные шаги, где автоматически учитывается микродвижение. Это зависит от начальной фазы встряхивания, которую мы установили равной нулю, как и в эксперименте. Чтобы получить прогноз для контуров динамического вихря, мы вычисляем перекрытие эволюционировавшего во времени состояния \(|\psi (t)\rangle = \hat U(t,0)|\psi (0)\rangle\) с исходное состояние | ψ (0)〉 и считать импульсы, где это перекрытие ниже порога 0,02. Эта процедура находит импульсы, при которых ожидаются динамические вихри с учетом неплоскостности полос, а конечный порог обусловлен численной реализацией. В последнем столбце дополнительного рисунка 1 эти числовые данные суммируются для всех временных шагов (с использованием разрешения в восемь временных шагов за период управления, чтобы лучше разрешить контуры). Фазовые диаграммы на рис. 3 и 8 получаются из этих точных чисел, а число Черна вычисляется как интеграл кривизны Берри. Нецелочисленные значения из расчета на конечной сетке в импульсном пространстве удаляются путем установки числа Черна равным нулю или единице на основе порога 0,5.
Нецелочисленные значения из расчета на конечной сетке в импульсном пространстве удаляются путем установки числа Черна равным нулю или единице на основе порога 0,5.
Описание сильной связи
Рассмотрим систему бесспиновых фермионов в гексагональной решетке со смещением подрешетки \({\mathrm{\Delta }} = \nu \hbar \omega + \hbar \delta\), которая почти резонансно приводимый в движение круговой силой }}(\omega t)\widehat {\mathbf{e}}_y]\) [см. рис. 2b]. Здесь ν — целое число, а \(\hbar \delta \ll \hbar \omega\) — расстройка. (Наш эксперимент описывается 9{\prime}\ell \rangle\), и где \(\delta _{\ell \in B}\) равно единице, если \(\ell\) лежит в подрешетке B , и нулю в противном случае. Поскольку мы не рассматриваем какие-либо голые скачки между ближайшими соседями, здесь мы опустили нижние индексы, используемые в основном тексте ( J ≡ J AB и Δ ≡ Δ AB) для упрощения записи. Сила F ( t ) является инерционной силой, создаваемой перемещением решетки по круговой орбите в пространстве, так что гамильтониан описывает систему в системе отсчета, движущуюся вместе с решеткой. 9{{\mathrm{rot}}}(t)} \hfill & { = — \nu \omega t\delta _{\ell \in B}.} \hfill \end{array}$$
9{{\mathrm{rot}}}(t)} \hfill & { = — \nu \omega t\delta _{\ell \in B}.} \hfill \end{array}$$
(11)
В то время как \(\hat U_{{\mathrm{shift}}}(t)\) интегрирует периодический во времени сдвиг квазиимпульса, вызванный круговой силой, \(\hat U_{{\mathrm{rot}} }(t)\) фиксирует поворот псевдоспина, определяемый степенью свободы подрешетки, и интегрирует резонансную часть \(\nu \hbar \omega\) дисбаланса подрешетки Δ. Результирующий преобразованный гамильтониан имеет вид
9{\prime}} — {\mathbf{r}}_\ell\), и \(\sigma _\ell = 1\) \(\left({\sigma _\ell = — 1} \right)\ ) для \(\ell \in A\) \(\left( {\ell \in B} \right)\). Преобразование сохраняет периодическую зависимость гамильтониана от времени и устраняет большие энергетические смещения порядка \(\hbar \omega\) между соседними узлами. При этом он обеспечивает хорошую отправную точку для вычисления эффективного стационарного гамильтониана \(\hat H _{\mathrm{F}}\) и периодического оператора микродвижения \(\hat U _{\mathrm{F}}(t) \) в высокочастотном приближении 9\dagger (0). $$
$$
(13)
Заметим, что преобразование \(\hat U(t)\) восстанавливает также трансляционную симметрию решетки, которая была нарушена внутренним потенциалом \(- {\mathbf{r}}_\ell \cdot {\mathbf{F}}(t)\), так что состояния Флоке \(\hat H\prime (t)\) и собственные состояния \(\ H_{\mathrm{F}}\) являются блоховскими состояниями.
Эффективный гамильтониан
Чтобы вычислить эффективный гамильтониан, мы сохраним два главных члена высокочастотного разложения 92(\alpha )} \right),$$
(19)
с координационным числом z = 3, имеет вклады обоих порядков.
Сравнение моделей с начальным смещением и без него
Существует принципиальное различие между случаем ν ≠ 0; соответствующий нашему эксперименту с ν = 1, и экспериментам со случаем ν = 0, описанным в работах. 27,46 . Для ν = 0 туннелирование ближайшего соседа уже присутствует в неуправляемой системе, а туннелирование ближайшего соседа второго порядка является процессом, индуцированным возбуждением.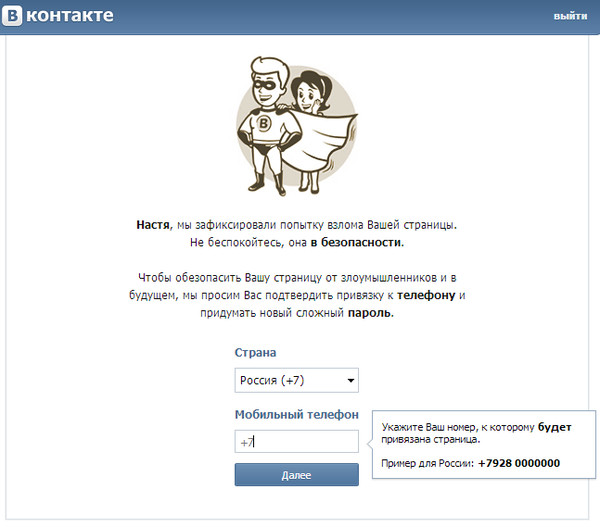 И наоборот, для 9{|н| + 2})\). Противоположный знак эффективного туннелирования следующего за ближайшим соседом на двух подрешетках возникает из-за противоположного знака смещения в промежуточное состояние в процессе сверхобмена. Это различие между случаями ν = 0 и ν = 1 имеет два основных следствия. Первый связан с тем, что фазы Пайерлса появляются на элементах матрицы туннелирования, вызванных возбуждением. Для ν = 0 эффективные элементы матрицы туннелирования следующего за ближайшим соседом являются комплексными, что соответствует конфигурации модели Холдейна 47 . В нашем случае при ν = 1 вместо ближайших соседей элементов туннельной матрицы приобретают фазу. Хотя модель все еще может быть преобразована в модель Холдейна с помощью калибровочного преобразования, это означает, что один из конусов Дирака смещается из одной из K точек в углу первой зоны Бриллюэна в точку Γ в ее центре. Второе следствие более важно: топологически нетривиальные свойства эффективного гамильтониана возникают из взаимодействия между процессами туннелирования ближайших соседей, с одной стороны, и процессами туннелирования следующих ближайших соседей, с другой.
И наоборот, для 9{|н| + 2})\). Противоположный знак эффективного туннелирования следующего за ближайшим соседом на двух подрешетках возникает из-за противоположного знака смещения в промежуточное состояние в процессе сверхобмена. Это различие между случаями ν = 0 и ν = 1 имеет два основных следствия. Первый связан с тем, что фазы Пайерлса появляются на элементах матрицы туннелирования, вызванных возбуждением. Для ν = 0 эффективные элементы матрицы туннелирования следующего за ближайшим соседом являются комплексными, что соответствует конфигурации модели Холдейна 47 . В нашем случае при ν = 1 вместо ближайших соседей элементов туннельной матрицы приобретают фазу. Хотя модель все еще может быть преобразована в модель Холдейна с помощью калибровочного преобразования, это означает, что один из конусов Дирака смещается из одной из K точек в углу первой зоны Бриллюэна в точку Γ в ее центре. Второе следствие более важно: топологически нетривиальные свойства эффективного гамильтониана возникают из взаимодействия между процессами туннелирования ближайших соседей, с одной стороны, и процессами туннелирования следующих ближайших соседей, с другой. Если энергетический масштаб одного из этих процессов намного меньше другого, топологическая ширина запрещенной зоны будет порядка этого меньшего энергетического масштаба. Для 92/(\hbar \omega )\) для большей движущей силы (до тех пор, пока α ≤ 1). Это говорит о том, что случай ν = 1 благоприятен для реализации робастных топологических зонных структур. Действительно, в работе ширина области с нетривиальным числом Черна составляет 100 Гц. 46 , но в этой работе 500 Гц. Однако в реализации с неоднородной решеткой, где условия резонанса глобального сотрясения варьируются по образцу, также имеет значение отношение ширины нетривиальной области к частоте возбуждения. 9\ dagger )} {\ kern 1pt} [h_0 ({\ mathbf {k}}) \ cdot \ hat I + {\ mathbf {h}} ({\ mathbf {k}}) \ cdot {\ mathbf {\ sigma }}]\left( {\begin{array}{*{20}{c}} {\шляпа a_{A{\mathbf{k}}}} \\ {\шляпа a_{B{\mathbf{k}} }}} \end{array}} \right).$$
Если энергетический масштаб одного из этих процессов намного меньше другого, топологическая ширина запрещенной зоны будет порядка этого меньшего энергетического масштаба. Для 92/(\hbar \omega )\) для большей движущей силы (до тех пор, пока α ≤ 1). Это говорит о том, что случай ν = 1 благоприятен для реализации робастных топологических зонных структур. Действительно, в работе ширина области с нетривиальным числом Черна составляет 100 Гц. 46 , но в этой работе 500 Гц. Однако в реализации с неоднородной решеткой, где условия резонанса глобального сотрясения варьируются по образцу, также имеет значение отношение ширины нетривиальной области к частоте возбуждения. 9\ dagger )} {\ kern 1pt} [h_0 ({\ mathbf {k}}) \ cdot \ hat I + {\ mathbf {h}} ({\ mathbf {k}}) \ cdot {\ mathbf {\ sigma }}]\left( {\begin{array}{*{20}{c}} {\шляпа a_{A{\mathbf{k}}}} \\ {\шляпа a_{B{\mathbf{k}} }}} \end{array}} \right).$$
(22)
Здесь \(\hat I\) — единичная матрица 2 × 2, σ обозначает вектор матриц Паули, действующих на псевдоспин пространство, определяемое двумя состояниями подрешетки σ = A , B и \(\ hat a _ {\ sigma {\ mathbf {k}}} = \ frac {1} {{\ sqrt M }} \ mathop {\sum}\nolimits_{\ell \in\sigma} e^{ — i{\mathbf{k}} \cdot {\mathbf{r}}_\ell}\hat a_\ell\) оператор уничтожения для фермиона с квазиимпульсом 93 2 {\ mathrm{sin}}({\mathbf{k}} \cdot {\mathbf{b}}_j) + {\mathrm{\Delta}}_{{\mathrm{eff}}}/2, $$
(26)
где a j — вектор, соединяющий сайты ближайшего соседа, где j обозначает три возможных направления движения от сайта A к сайту B сайт , \({\mathbf{a}}_j = a[{\mathrm{cos}}(\varphi _j)\widehat {\mathbf{e}}_x + {\mathrm{sin}}(\varphi _j )\widehat {\mathbf{e}}_y]\) с соответствующими углами φ j определяется по положительной оси x . b j обозначает векторы решетки \({\mathbf{b}}_1 = a(\sqrt 3 ,0),{\mathbf{b}}_2 = a\left( { — \frac{ {\ sqrt 3} {2}, \ frac {3} {2}} \ right), {\ mathbf {b}} _3 = — {\ mathbf {b}} _1 — {\ mathbf {b}} _2 \), которые соединяют ближайших соседей, а c 0, z ( α ) являются некоторыми константами, полученными из суммы в уравнении. (18).
b j обозначает векторы решетки \({\mathbf{b}}_1 = a(\sqrt 3 ,0),{\mathbf{b}}_2 = a\left( { — \frac{ {\ sqrt 3} {2}, \ frac {3} {2}} \ right), {\ mathbf {b}} _3 = — {\ mathbf {b}} _1 — {\ mathbf {b}} _2 \), которые соединяют ближайших соседей, а c 0, z ( α ) являются некоторыми константами, полученными из суммы в уравнении. (18).
Микродвижение 9\ dagger ) {\ kern 1pt} [g_x ({\ mathbf {k}}, t) \ sigma _x + g_y ({\ mathbf {k}}, t) \ sigma _y] \ left ( {\ begin {array} {*{20}{c}} {\шляпа a_{A{\mathbf{k}}}} \\ {\шляпа a_{B{\mathbf{k}}}} \end{массив}} \right) . $$
(29)
Здесь, G x ( K , T ) = RE ( G ( K , T )) и  } \hfill \end{array}$$
} \hfill \end{array}$$
(30)
Для небольших управляющих амплитуд α основной вклад происходит от члена m = −1. Если пренебречь всеми остальными условиями, \(\hat U_{\mathrm{F}}(t)\) описывает вращение в псевдоспине на угол, зависящий от k \(\sim J/(\hbar \omega )\) вокруг оси в плоскости xy , которая сама вращается вокруг z — ось с угловой скоростью ω и k -зависимая фаза. Однако при увеличении α для \(\alpha \simeq 1\) как член m = −2, так и член m = 1 становятся релевантными, так что более высокие гармоники частоты возбуждения дадут о себе знать в микродвижение, описываемое \(\hat U _{\mathrm{F}}(t)\).
Помимо микродвижения в реальном пространстве, описываемого выражением \(\hat U_{\mathrm{F}}(t)\), еще один вклад в микродвижение дает преобразование \(\hat U(t) = \hat U_{{\mathrm{shift}}}(t)\hat U_{{\mathrm{rot}}}(t)\) обратно в исходную решетчатую систему отсчета. Он описывает фазовое вращение между различными узлами решетки, которое соответствует как сдвигу квазиимпульса, так и вращению вокруг оси z псевдоспина подрешетки. 2)\) и атомная масса 9{\mathrm{t}}\hat U_{{\mathrm{micro}}}(t)\), теперь ясно, что эти томографические и исходные гамильтонианы равны друг другу только для моментов томографирования t = t 0 + нТл с целым числом n . Для любых других субстробоскопических временных шагов гамильтониан томографии не будет параллелен исходному гамильтониану на сфере Блоха. На рис. 4а основного текста мы опускаем эти вклады из-за микродвижения и просто стремимся проиллюстрировать экспериментальную процедуру. 9{\mathrm{t}}\) представлен зависящим от квазиимпульса вектором h t ( k ), играющим роль магнитного поля относительно псевдоспина подрешетки и состояния | ψ ( t )〉 представлен зависящим от квазиимпульса единичным вектором ψ ( t ), обозначающим точку на сфере Блоха этого псевдоспина. Положения измеренных вихрей соответствуют тем точкам в k -пространстве, где оба вектора параллельны (или антипараллельны).
2)\) и атомная масса 9{\mathrm{t}}\hat U_{{\mathrm{micro}}}(t)\), теперь ясно, что эти томографические и исходные гамильтонианы равны друг другу только для моментов томографирования t = t 0 + нТл с целым числом n . Для любых других субстробоскопических временных шагов гамильтониан томографии не будет параллелен исходному гамильтониану на сфере Блоха. На рис. 4а основного текста мы опускаем эти вклады из-за микродвижения и просто стремимся проиллюстрировать экспериментальную процедуру. 9{\mathrm{t}}\) представлен зависящим от квазиимпульса вектором h t ( k ), играющим роль магнитного поля относительно псевдоспина подрешетки и состояния | ψ ( t )〉 представлен зависящим от квазиимпульса единичным вектором ψ ( t ), обозначающим точку на сфере Блоха этого псевдоспина. Положения измеренных вихрей соответствуют тем точкам в k -пространстве, где оба вектора параллельны (или антипараллельны).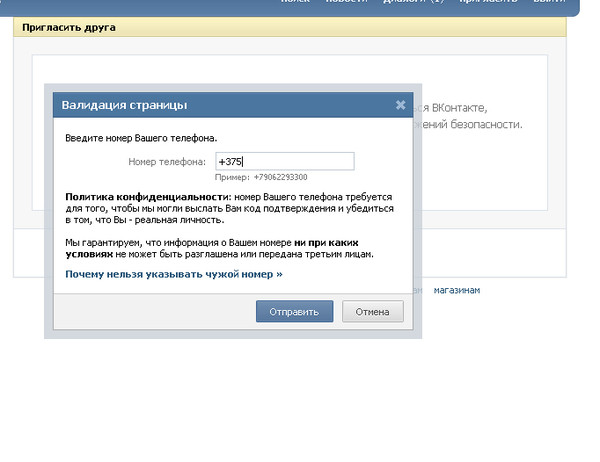 Таким образом, пока h t ( k ) везде указывает на южный (или северный) полюс, вращение псевдоспина \(\hat U_{{\mathrm{rot}}}(t)\) с угловой скоростью ω не даст о себе знать. Однако, как только h t ( k ) отклонится от северного полюса, как это имеет место в данном эксперименте, это вращение вызовет колебательное поведение положения вихря относительно времени т . Таким образом, взаимодействие между колебаниями, вызванными \(\hat U_{\mathrm{F}}(t)\) и \(\hat U_{{\mathrm{rot}}}(t)\), является еще одним источник для генерации высших гармоник в движении вихревого положения, наблюдаемого в эксперименте.
Таким образом, пока h t ( k ) везде указывает на южный (или северный) полюс, вращение псевдоспина \(\hat U_{{\mathrm{rot}}}(t)\) с угловой скоростью ω не даст о себе знать. Однако, как только h t ( k ) отклонится от северного полюса, как это имеет место в данном эксперименте, это вращение вызовет колебательное поведение положения вихря относительно времени т . Таким образом, взаимодействие между колебаниями, вызванными \(\hat U_{\mathrm{F}}(t)\) и \(\hat U_{{\mathrm{rot}}}(t)\), является еще одним источник для генерации высших гармоник в движении вихревого положения, наблюдаемого в эксперименте.
Знак числа зацепления
Знак числа зацепления определяем путем сравнения относительной киральности статического ( χ s ) и динамического вихрей ( χ d ), т.е. суммарный знак равен устанавливается х с х д . Хиральность контура динамического вихря определяется произведением киральности вихря (или антивихря) х v и киральности пройденного им пути х р .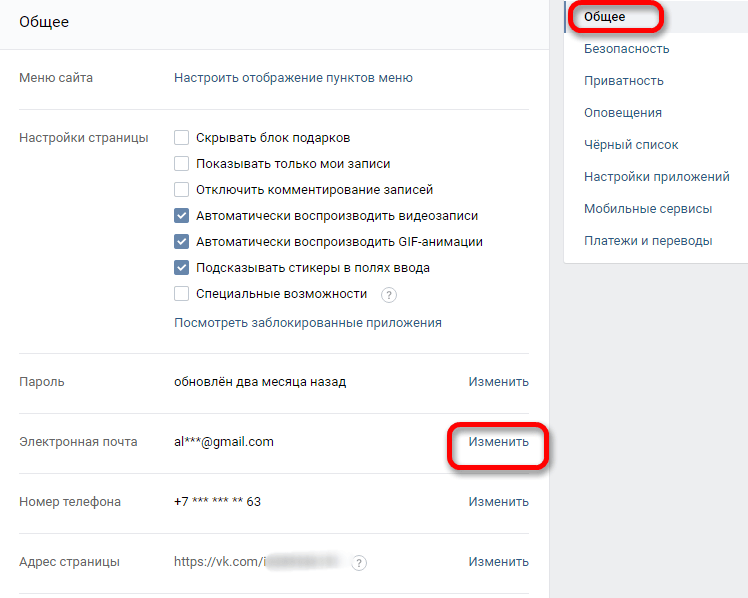 Поскольку контур динамического вихря является прообразом экватора сферы Блоха, направление движения задается градиентом гамильтониана | ч ( к v )| на экваторе. Это направление можно изменить, изменив величину параметра зазора | h ( k v )|, без закрытия щели в самой точке Дирака, т.е. без изменения киральности статического вихря в точке Дирака. Далее мы покажем, что изменение градиента гамильтониана на экваторе также превращает вихри в антивихри и, следовательно, сохраняет киральность х d , а вместе с тем и знак связующего числа. Это означает, что киральность динамического вихревого контура х d действительно отражает топологию гамильтониана и не может быть изменена топологически тривиальными деформациями энергетической зоны. Наши определения вдохновлены родственным аргументом в исх. 15 .
Поскольку контур динамического вихря является прообразом экватора сферы Блоха, направление движения задается градиентом гамильтониана | ч ( к v )| на экваторе. Это направление можно изменить, изменив величину параметра зазора | h ( k v )|, без закрытия щели в самой точке Дирака, т.е. без изменения киральности статического вихря в точке Дирака. Далее мы покажем, что изменение градиента гамильтониана на экваторе также превращает вихри в антивихри и, следовательно, сохраняет киральность х d , а вместе с тем и знак связующего числа. Это означает, что киральность динамического вихревого контура х d действительно отражает топологию гамильтониана и не может быть изменена топологически тривиальными деформациями энергетической зоны. Наши определения вдохновлены родственным аргументом в исх. 15 .
Состояние системы ψ ( k , t ) определяется уравнением. (5) для θ ( 9{\mathrm{f}}({\mathbf{k}})\) лежит на экваторе, так что для α ( k , t n ) = nπ и ω= nπ ( k , t n ) points to the north (south) pole for odd (even) integers n , where t n = nπ /2| ч ф ( к )|. Далее мы сосредоточимся на случае n = 1, где динамический вихрь обнаружен в момент времени т 1 ( к ). Условие α ( k , t n ) = π определяет траектории динамических вихрей в обратном образе ), экватора сферы Блоха относительно отображения \(\widehat {\mathbf{h}}({\mathbf{k}}):\,{\mathbf{k}} \to \widehat {\ mathbf{ч}}\). Обратите внимание, что в исх. 15 , это соответствует прообразу северного полюса относительно карты \([{\mathbf{k}},t] \to \widehat {\mathbf{h}}\).
(5) для θ ( 9{\mathrm{f}}({\mathbf{k}})\) лежит на экваторе, так что для α ( k , t n ) = nπ и ω= nπ ( k , t n ) points to the north (south) pole for odd (even) integers n , where t n = nπ /2| ч ф ( к )|. Далее мы сосредоточимся на случае n = 1, где динамический вихрь обнаружен в момент времени т 1 ( к ). Условие α ( k , t n ) = π определяет траектории динамических вихрей в обратном образе ), экватора сферы Блоха относительно отображения \(\widehat {\mathbf{h}}({\mathbf{k}}):\,{\mathbf{k}} \to \widehat {\ mathbf{ч}}\). Обратите внимание, что в исх. 15 , это соответствует прообразу северного полюса относительно карты \([{\mathbf{k}},t] \to \widehat {\mathbf{h}}\).
Направление движения вихря .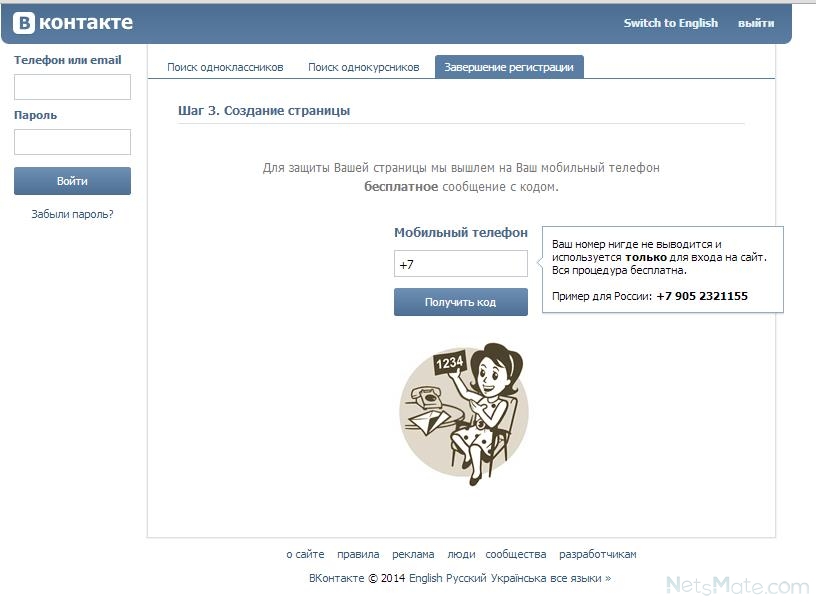 Пусть \({\mathbf{k}}_{\mathrm{v}} \in {\kern 1pt} \ell \subset {\Bbb Z}\) — точка на прямой \(\ell\), лежащей в прообразе экватора и \(\widehat {\mathbf{e}}_{||}({\mathbf{k}}_{\mathrm{v}})\) обозначают единичный касательный вектор \ (\ell\) at k v , который определяет направление на этой линии. Тогда вихрь, прошедший k v за время t ( k v ), движется со скоростью \(\dot{\mathbf{k}}_{\mathrm{v}} = \dot k_{||}\widehat {\mathbf{e}}_{||}\), где \(\dot k_{||} = — \omega ({\mathbf{k}}_{\mathrm{v} })/|{\mathbf{g}}_{||}({\mathbf{k}}_{\mathrm{v}})|\) с \({\mathbf{g}}_{|| } ({\ mathbf {k}}) = t ({\ mathbf {k}}) \ nabla _ {\ mathbf {k}} \ omega ({\ mathbf {k}}) \ cdot \ widehat {\ mathbf { e}}_{||}({\mathbf{k}}_{\mathrm{v}})\). Таким образом, пока зазор не закрывается \([\omega ({\mathbf{k}}) > 0]\), направление движения 9{\ mathrm {f}} ({\ mathbf {k}}) \).
Пусть \({\mathbf{k}}_{\mathrm{v}} \in {\kern 1pt} \ell \subset {\Bbb Z}\) — точка на прямой \(\ell\), лежащей в прообразе экватора и \(\widehat {\mathbf{e}}_{||}({\mathbf{k}}_{\mathrm{v}})\) обозначают единичный касательный вектор \ (\ell\) at k v , который определяет направление на этой линии. Тогда вихрь, прошедший k v за время t ( k v ), движется со скоростью \(\dot{\mathbf{k}}_{\mathrm{v}} = \dot k_{||}\widehat {\mathbf{e}}_{||}\), где \(\dot k_{||} = — \omega ({\mathbf{k}}_{\mathrm{v} })/|{\mathbf{g}}_{||}({\mathbf{k}}_{\mathrm{v}})|\) с \({\mathbf{g}}_{|| } ({\ mathbf {k}}) = t ({\ mathbf {k}}) \ nabla _ {\ mathbf {k}} \ omega ({\ mathbf {k}}) \ cdot \ widehat {\ mathbf { e}}_{||}({\mathbf{k}}_{\mathrm{v}})\). Таким образом, пока зазор не закрывается \([\omega ({\mathbf{k}}) > 0]\), направление движения 9{\ mathrm {f}} ({\ mathbf {k}}) \).
Вихревая хиральность . Для получения киральности динамического вихря в точке k v разложим волновую функцию ψ ( k v , t ( k 9104)) в окрестности 5 1 из k v ,
$${\mathbf{\psi}}({\mathbf{k}}) = \left( {\begin{array}{*{20}{c}} 0 \ \ 0 \\ { — 1} \end{массив}} \right) + \delta {\mathbf{k}}\left( {\begin{array}{*{20}{c}} {\hat h_x^ {\ mathrm {f}} ({\ mathbf {k}} _ {\ mathrm {v}}) {\ mathbf {f}} ({\ mathbf {k}} _ {\ mathrm {v}}) — \ шляпа h_y ^ {\ mathrm {f}} ({\ mathbf {k}} _ {\ mathrm {v}}) {\ mathbf {g}} ({\ mathbf {k}} _ {\ mathrm {v}} )} \\ {\ шляпа h_y ^ {\ mathrm {f}} ({\ mathbf {k}} _ {\ mathrm {v}}) {\ mathbf {f}} ({\ mathbf {k}} _ { \ mathrm {v}}) — \ шляпа h_x ^ {\ mathrm {f}} ({\ mathbf {k}} _ {\ mathrm {v}}) {\ mathbf {g}} ({\ mathbf {k} }_{\mathrm{v}})} \\ 0 \end{массив}} \right),$$ 9{\ mathrm {f}} ({\ mathbf {k}}) \) и г ( к v ) = π / ( ч ( к ) 9 8 910 9 8 0 | h ( k )|) как и прежде.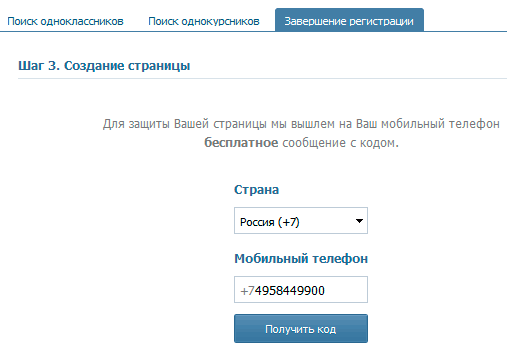 Это также может быть выражено как }) \ delta {\ mathbf {k}} \ widehat {\ mathbf {h}} ({\ mathbf {k}}) + {\ mathbf {g}} ({\ mathbf {k}} _ {\ mathrm { v}})\delta {\mathbf{k}}\widehat {\mathbf{h}}\prime ({\mathbf{k}})\), где \(\widehat {\mathbf{h}}\prime ({\mathbf{k}}) = ( — \widehat {\mathbf{h}}_y({\mathbf{k}}_{\mathrm{v}}),\widehat {\mathbf{h}}_x ({\mathbf{k}}_{\mathrm{v}}}}\) — единичный вектор, ортогональный \(\widehat {\mathbf{h}}({\mathbf{k}}_{\mathrm{ v}})\) и который, как и \(\widehat {\mathbf{h}}({\mathbf{k}}_{\mathrm{v}})\), лежит на экваторе. Эти два единичных вектора \(\left({\widehat {\mathbf{h}},\widehat {\mathbf{h}}\prime} \right)\) охватывают систему координат, которая повернута на ϕ ( k v ) относительно натянутого на \(\left( {\widehat {\mathbf{e}}_x,{\kern 1pt} \widehat {\mathbf{e}}_y } \Правильно)\).
Это также может быть выражено как }) \ delta {\ mathbf {k}} \ widehat {\ mathbf {h}} ({\ mathbf {k}}) + {\ mathbf {g}} ({\ mathbf {k}} _ {\ mathrm { v}})\delta {\mathbf{k}}\widehat {\mathbf{h}}\prime ({\mathbf{k}})\), где \(\widehat {\mathbf{h}}\prime ({\mathbf{k}}) = ( — \widehat {\mathbf{h}}_y({\mathbf{k}}_{\mathrm{v}}),\widehat {\mathbf{h}}_x ({\mathbf{k}}_{\mathrm{v}}}}\) — единичный вектор, ортогональный \(\widehat {\mathbf{h}}({\mathbf{k}}_{\mathrm{ v}})\) и который, как и \(\widehat {\mathbf{h}}({\mathbf{k}}_{\mathrm{v}})\), лежит на экваторе. Эти два единичных вектора \(\left({\widehat {\mathbf{h}},\widehat {\mathbf{h}}\prime} \right)\) охватывают систему координат, которая повернута на ϕ ( k v ) относительно натянутого на \(\left( {\widehat {\mathbf{e}}_x,{\kern 1pt} \widehat {\mathbf{e}}_y } \Правильно)\).
Хиральность χ v динамического вихря теперь определяется тем, движется ли азимутальная фаза ϕ ( k ) в положительном или отрицательном направлении, а δ k берется по замкнутому контуру; \(\ delta {\ mathbf {k}} = \ delta k [{\ mathrm {cos}} (\ gamma) \ widehat {\ mathbf {e}} _x + {\ mathrm {sin}} (\ gamma) \ широкая шляпа {\mathbf{e}}_y]\) на γ : 0 → 2 π . Хиральность гласит:
Хиральность гласит:
$$\chi _{\mathrm{v}} = {\mathrm{sgn}}[{\mathbf{g}}({\mathbf{k}}_{\mathrm{v}} ) \times {\mathbf{f}}({\mathbf{k}}_{\mathrm{v}})] = {\mathrm{sgn}}[{\mathbf{g}}({\mathbf{k }}_{\mathrm{v}}) \cdot \widehat {\mathbf{e}}_{||}].$$
(37)
Следовательно, направление движения вихря и его киральность зависят на градиенте g ( k v ) щели в положении вихря k против . Инверсия направления движения требует инвертирования градиента зазора g || ( k v ) по линии \(\ell\). С другой стороны, инвертирование хиральности вихря путем замены г ( k v ) требует обращения \({\mathbf{g}}({\mathbf{k}}_{\mathrm {v}}) \cdot {\mathbf{f}}_ \bot ({\mathbf{k}}_{\mathrm{v}}) \equiv {\mathbf{g}}_{{\mathbf{f }}_ \bot}({\mathbf{k}}_{\mathrm{v}})\). Обратите внимание, что единичный вектор \(\widehat {\mathbf{e}}_{||}\), который определен так, чтобы указывать в направлении, где \(\hat h_z^{\mathrm{f}}({\mathbf {k}}_{\mathrm{v}})\) сохраняет постоянное значение равным нулю, стоит перпендикулярно градиенту \(\hat h_z^{\mathrm{f}}({\mathbf{k}}_{ \mathrm{v}})\).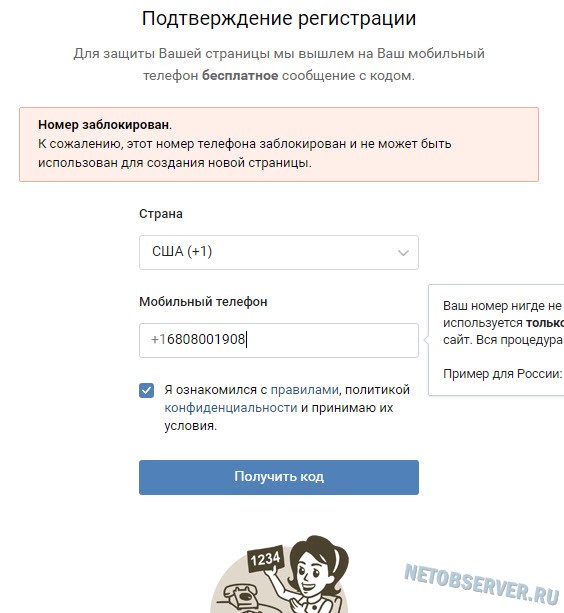 Таким образом, изменение направления движения вихря без закрытия щели означает, что вихрь меняет свою киральность, что сохраняет общий знак динамического вихревого контура х v х р . Следовательно, любая деформация гамильтониана, не меняющая топологию, не может изменить наблюдаемый знак числа зацепления.
Таким образом, изменение направления движения вихря без закрытия щели означает, что вихрь меняет свою киральность, что сохраняет общий знак динамического вихревого контура х v х р . Следовательно, любая деформация гамильтониана, не меняющая топологию, не может изменить наблюдаемый знак числа зацепления.
Наличие данных
Исходные данные для рис. 3–6 и 8–10 представлены как файл исходных данных в дополнительном материале. Все файлы данных доступны у соответствующего автора по запросу.
Ссылки
Хасан, М. З. и Кейн, К. Л. Коллоквиум: Топологические изоляторы. Ред. Мод. физ. 82 , 3045 (2010).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Лин, Ю.-Дж., Хименес-Гарсия, К. и Спилман, И.Б. Спин-орбитально-связанные конденсаты Бозе-Эйнштейна. Природа 471 , 83 (2011).

ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Струк, Дж. и др. Квантовое моделирование фрустрированного классического магнетизма в треугольных оптических решетках. Наука 333 , 996 (2011).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Струк, Дж. и др. Перестраиваемый калибровочный потенциал для нейтральных и бесспиновых частиц в управляемых оптических решетках. Физ. Преподобный Летт. 108 , 225304 (2012).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Джоцу, Г. и др. Экспериментальная реализация топологической модели Холдейна с ультрахолодными фермионами. Природа 515 , 237 (2014).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
- «>
Aidelsburger, M. et al. Экспериментальная реализация сильных эффективных магнитных полей в оптической решетке. Физ. Преподобный Летт. 107 , 255301 (2011).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Мияке, Х., Сивилоглу, Г. А., Кеннеди, Дж., Бертон, В. К. и Кеттерле, В. Реализация гамильтониана Харпера с помощью лазерного туннелирования в оптических решетках. физ. Преподобный Летт. 111 , 185302 (2013).
ОБЪЯВЛЕНИЕ Статья Google ученый
Fläschner, N. et al. Экспериментальная реконструкция кривизны Берри в полосе Флоке-Блоха. Наука 352 , 1091 (2016).
ОБЪЯВЛЕНИЕ Статья Google ученый
Tarnowski, M. et al. Наблюдение топологических дефектов блоховского состояния и их сливающийся переход.
 физ. Преподобный Летт. 118 , 240403 (2017).
физ. Преподобный Летт. 118 , 240403 (2017).ОБЪЯВЛЕНИЕ Статья Google ученый
Купер, Н. Р. и Далибард, Дж. Достижение дробных квантовых холловских состояний с помощью решеток оптических потоков. Физ. Преподобный Летт. 110 , 185301 (2013).
ОБЪЯВЛЕНИЕ Статья Google ученый
Грушин А. Г., Гомес-Леон А. & Neupert, T. Дробные изоляторы Черна Флоке. физ. Преподобный Летт. 112 , 156801 (2014).
ОБЪЯВЛЕНИЕ Статья Google ученый
Анисимовас Э., Жлабис Г., Андерсон Б. М., Юзелюнас Г. и Эккардт А. Роль микродвижения в реальном пространстве для бозонных и фермионных дробных изоляторов Черна Флоке. Физ. B 91 , 245135 (2015).
ОБЪЯВЛЕНИЕ Статья Google ученый
- «>
Aidelsburger, M. et al. Измерение числа Черна полос Хофштадтера с ультрахолодными бозонными атомами. Нац. физ. 11 , 162 (2015).
КАС Статья Google ученый
Астерия, Л. и др. Измерение квантованного кругового дихроизма в ультрахолодной топологической материи. Нац. физ. . https://doi.org/10.1038/s41567-019-0417-8 (2019 г.).
Артикул Google ученый
Ван, К., Чжан, П., Чен, X., Ю, Дж. и Чжай, Х. Схема измерения топологического числа изолятора Черна из Quench Dynamics. Физ. Преподобный Летт. 118 , 185701 (2017).
ОБЪЯВЛЕНИЕ Статья Google ученый
Fläschner, N. et al. Наблюдение динамических вихрей после закалки в системе с топологией. Нац. физ. 14 , 265 (2018).
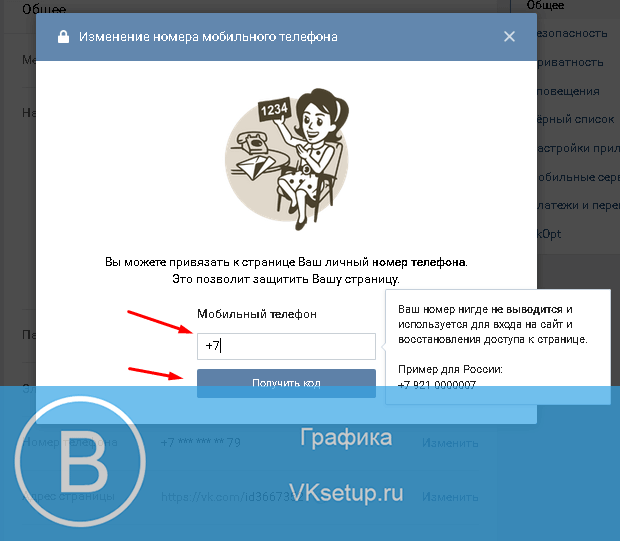
Артикул Google ученый
Сан, В. и др. Раскройте топологию от Quantum Quench Dynamics. Физ. Преподобный Летт. 121 , 250403 (2018).
ОБЪЯВЛЕНИЕ Статья Google ученый
Солтан-Панахи, П. и др. Многокомпонентные квантовые газы в спин-зависимых гексагональных решетках. Нац. физ. 7 , 434 (2011).
КАС Статья Google ученый
Эккардт А., Вайс К. и Хольтхаус М. Переход сверхтекучий изолятор в оптической решетке с периодическим возбуждением. Физ. Преподобный Летт. 95 , 260404 (2005).
ОБЪЯВЛЕНИЕ Статья Google ученый
Lignier, H. et al. Динамическое управление туннелированием материи-волны в периодических потенциалах.
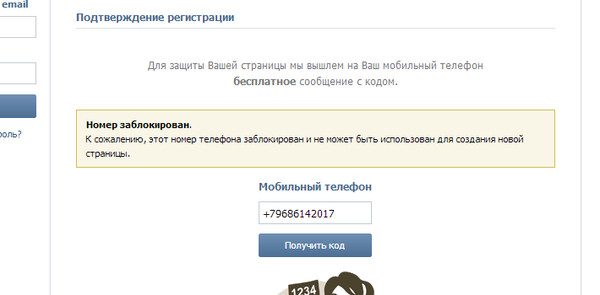 Физ. Преподобный Летт. 99 , 220403 (2007).
Физ. Преподобный Летт. 99 , 220403 (2007).ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Паркер, К.В., Ха, Л.К. и Чин, К. Прямое наблюдение эффективных ферромагнитных доменов холодных атомов в сотрясенной оптической решетке. Нац. физ. 9 , 769 (2013).
КАС Статья Google ученый
Голдман, Н. и Далибард, Дж. Периодически управляемые квантовые системы: эффективные гамильтонианы и инженерные калибровочные поля. Физ. Ред. X. 4 , 031027 (2014).
Google ученый
Буков М., Д’Алессио Л. и Полковников А. Универсальное высокочастотное поведение периодически управляемых систем: от динамической стабилизации до техники Флоке. Доп. физ. 64 , 139 (2015).
ОБЪЯВЛЕНИЕ Статья Google ученый
- «>
Эккардт, А. и Анисимовас, Э. Высокочастотное приближение для периодически управляемых квантовых систем с точки зрения пространства Флоке. New J. Phys. 17 ,
(2015).
Артикул Google ученый
Эккардт, А. Коллоквиум: Атомные квантовые газы в периодически управляемых оптических решетках. Ред. Мод. физ. 89 , 011004 (2017).
ОБЪЯВЛЕНИЕ MathSciNet Статья Google ученый
Ока, Т. и Аоки, Х. Фотогальванический эффект Холла в графене. физ. Ревизия B . 79 , 081406(R) (2009).
ОБЪЯВЛЕНИЕ Статья Google ученый
Rechtsman, M.C. et al. Фотонные топологические изоляторы Флоке. Природа 496 , 196 (2013).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
- «>
Холдейн, Ф. Д. М. Модель квантового эффекта Холла без уровней Ландау: реализация аномалии четности в конденсированной среде. физ. Преподобный Летт. 61 , 2015 (1988).
ОБЪЯВЛЕНИЕ MathSciNet КАС Статья Google ученый
Хауке, П., Левенштейн, М. и Эккардт, А. Томография ленточных изоляторов по динамике гашения. Физ. Преподобный Летт. 113 , 045303 (2014).
ОБЪЯВЛЕНИЕ Статья Google ученый
Альба, Э., Фернандес-Гонзальво, X., Мур-Пети, Дж., Пачос, Дж. К. и Гарсия-Риполл, Дж. Дж. Наблюдение топологического порядка в измерениях времени пролета. физ. Преподобный Летт. 107 , 235301 (2011).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Ю. Дж. Фазовые вихри закаленной модели Холдейна.
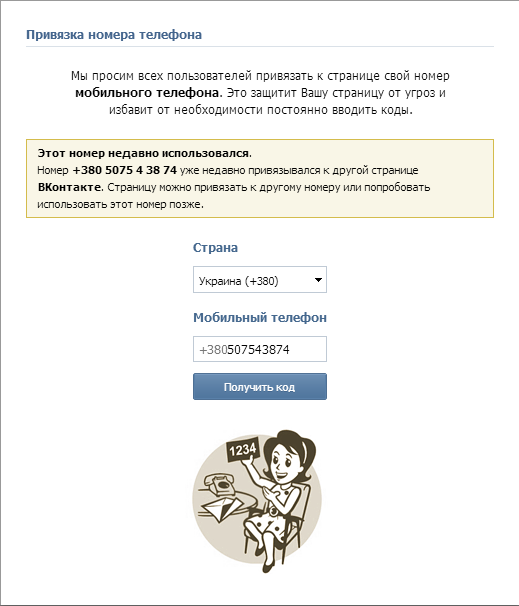 Физ. Ред. А. 96 , 023601 (2017).
Физ. Ред. А. 96 , 023601 (2017).ОБЪЯВЛЕНИЕ Статья Google ученый
Д’Алессио, Л. и Ригол, М. Динамическая подготовка изоляторов Флоке Черна. Нац. коммун. 6 , 8336 (2015).
ОБЪЯВЛЕНИЕ Статья Google ученый
Кайо, М. Д., Купер, Н. Р. и Бхасин, М. Дж. Квантовое подавление в изоляторах Черна. Физ. Преподобный Летт. 115 , 236403 (2015).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Ху, Ю., Золлер, П. и Будич, Дж. К. Динамическое построение квантованного отклика Холла из нетопологических состояний. физ. Преподобный Летт. 117 , 126803 (2016).
ОБЪЯВЛЕНИЕ Статья Google ученый
- «>
Юнал, Ф. Н., Мюллер, Э. Дж. и Октел, М. О. Неравновесный фракционный отклик Холла после топологического гашения. Физ. Ред. А. 94 , 053604 (2016).
ОБЪЯВЛЕНИЕ Статья Google ученый
МакГинли М. и Купер Н. Р. Топология одномерных квантовых систем вне равновесия. физ. Преподобный Летт. 121 , 0
(2018).ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Юань X. X. и др. Наблюдение за топологическими связями, связанными с изоляторами Хопфа, в твердотельном квантовом симуляторе. Подбородок. физ. лат. 34 , 060302 (2017).
ОБЪЯВЛЕНИЕ Статья Google ученый
Стиклет, Д. и Пьешон, Ф. Прыжки от дальнего соседа в моделях графена и Холдейна. физ. Re.v B. 87 , 115402 (2013).

ОБЪЯВЛЕНИЕ Статья Google ученый
Бена, К. и Саймон, Л. Метаморфозы точек Дирака от связей третьего соседа в графене и родственных материалах. Физ. Rev. B. 83 , 115404 (2011).
ОБЪЯВЛЕНИЕ Статья Google ученый
Бхаттачарья У., Хатчинсон Дж. и Датта А. Тушение в изоляторах Черна с помощью спутниковых точек Дирака: судьба краевых состояний. физ. Ред. Б. 95 , 144304 (2017).
ОБЪЯВЛЕНИЕ Статья Google ученый
Миками Т. и др. Теория Бриллюэна-Вигнера для высокочастотного расширения в системах с периодическим возбуждением: приложение к топологическим изоляторам Флоке. Физ. Ред. Б. 93 , 144307 (2016).
ОБЪЯВЛЕНИЕ Статья Google ученый
- «>
Desbuquois, R. et al. Управление населенностью состояния Флоке и наблюдение микродвижения в квантовой системе с двумя телами, управляемой периодически. физ. Ред. А. 96 , 053602 (2017).
ОБЪЯВЛЕНИЕ Статья Google ученый
Руднер, М.С., Линднер, Н.Х., Берг, Э. и Левин, М. Аномальные краевые состояния и объемно-краевое соответствие для периодически управляемых двумерных систем. Физ. Ред. X . 3 , 031005 (2013).
КАС Google ученый
Quelle, A., Weitenberg, C., Sengstock, K. & Smith, C.M. Ведущий протокол для топологической фазы Флоке без статического аналога. New J. Phys. 19 , 113010 (2017).
ОБЪЯВЛЕНИЕ Статья Google ученый
Huang, Z. & Baltsky, A. V. Phys. Преподобный Летт.
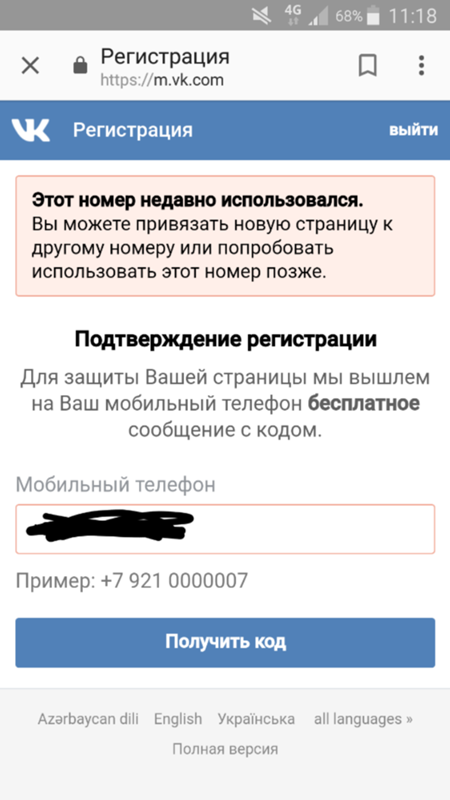 117 , 086802 (2016).
117 , 086802 (2016).ОБЪЯВЛЕНИЕ Статья Google ученый
Джоцу, Г. и др. Экспериментальная реализация топологической модели Холдейна с ультрахолодными фермионами. Природа 515 , 237 (2014).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Холдейн, Ф. Д. М. Модель квантового эффекта Холла без уровней Ландау: реализация «аномалии четности» в конденсированной среде. Физ. Преподобный Летт. 61 , 2015 (1988).
ОБЪЯВЛЕНИЕ MathSciNet КАС Статья Google ученый
Скачать ссылки
Благодарности
Это исследование финансировалось Deutsche Forschungsgemeinschaft (DFG, Немецкий исследовательский фонд) через Исследовательское подразделение FOR 2414 под номером проекта 277974659 и через Кластер передового опыта «Гамбургский центр сверхбыстрой визуализации — структура, динамика и контроль материи в атомная шкала» под номером проекта 194651731. Б.С.Р. признает финансовую поддержку со стороны Европейской комиссии (стипендия Марии Кюри). Мы признательны Раманджиту Сохалу и Кристофу Стратеру за плодотворные обсуждения.
Б.С.Р. признает финансовую поддержку со стороны Европейской комиссии (стипендия Марии Кюри). Мы признательны Раманджиту Сохалу и Кристофу Стратеру за плодотворные обсуждения.
Информация об авторе
Примечания автора
Эти авторы внесли равный вклад: Matthias Tarnowski, F. Nur Ünal.
Авторы и принадлежности
Институт Für Laserphysik, Universität Hamburg, 22761, Hamburg, Germany
Matthias Tarnowski, Nickenrug.9002
For Weit.9002 For Weit. Imaging, 22761, Гамбург, Германия
Matthias Tarnowski, Nick Fläschner, Benno S. Rem, Klaus Sengstock и Christof Weitenberg
Max-Planck-Institut für Physik komplexer Systeme, Nöthnitzer Straße 38, 01187, Dresden & Feckrénal, Germany
3.
Zentrum für Optische Quantentechnologien, Universität Hamburg, 22761, Гамбург, Германия0003
Вы также можете искать этого автора в PubMed Google Scholar
- F.
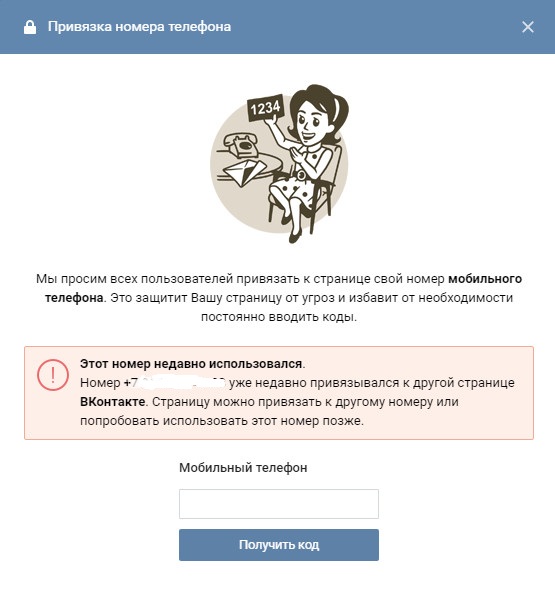 Nur Ünal
Nur ÜnalПросмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Nick Fläschner
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Benno S. Rem
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- André Eckardt
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Klaus Sengstock
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Christof Weitenberg
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Взносы
М.Т., Н.Ф. и Б.С.Р. взяли и проанализировали данные и выполнили численные расчеты. Ф.Н.Ю. и А.Е. выполнили аналитические расчеты и выводы. К.В., К.С. и А.Е. руководили работой. Все авторы внесли свой вклад в обсуждение результатов и в написание рукописи.
Ф.Н.Ю. и А.Е. выполнили аналитические расчеты и выводы. К.В., К.С. и А.Е. руководили работой. Все авторы внесли свой вклад в обсуждение результатов и в написание рукописи.
Автор, ответственный за переписку
Клаус Сенгшток.
Декларации этики
Конкурирующие интересы
Авторы заявляют об отсутствии конкурирующих интересов.
Дополнительная информация
Информация о рецензировании журнала : Nature Communications благодарит анонимных рецензентов за их вклад в рецензирование этой работы.
Примечание издателя: Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Дополнительная информация
Дополнительная информация
Исходные данные
Исходные данные
Права и разрешения
Открытый доступ формате, если вы укажете автора(ов) оригинала и источник, предоставите ссылку на лицензию Creative Commons и укажите, были ли внесены изменения.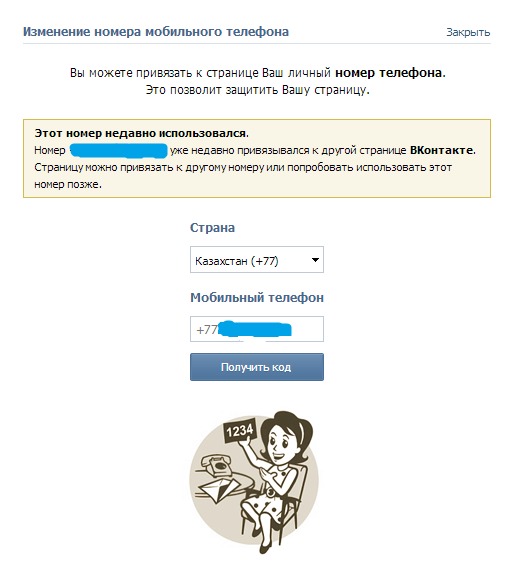 Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons для статьи, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.
Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons для статьи, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.
Перепечатка и разрешения
Об этой статье
Эта статья цитируется
Биморфные топологические изоляторы Флоке
- Георгиос Г. Пириалакос
- Юлиус Бек
- Деметриос Н.
 Христодулидес
Христодулидес
Природные материалы (2022)
Индикаторы динамической симметрии для кристаллов Флоке
- Цзябин Юй
- Жуй-Син Чжан
- Чжи-Да Сонг
Nature Communications (2021)
Исследование объемных топологических инвариантов с использованием фотонных решеток с утечками
- Даниэль Лейкам
- Дарья Александровна Смирнова
Физика природы (2021)
Аномальные и нормальные дислокационные моды в топологических изоляторах Флоке
- Танай Наг
- Битан Рой
Физика связи (2021)
Топологические особенности без решетки в спин-орбитально связанных атомах Рашбы
- А.
 Вальдес-Кюриэль
Вальдес-Кюриэль - Д. Трипогеоргос
- И. Б. Шпильман
Nature Communications (2021)
- А.
Комментарии
Отправляя комментарий, вы соглашаетесь соблюдать наши Условия и Правила сообщества. Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое.
Скачать PDF
Номер связи — wikidoc
Файл:3D-Link.PNG
Две кривые этой (2,4)-торической связи имеют номер связи четыре.
В математике число связи — это числовой инвариант, описывающий соединение двух замкнутых кривых в трехмерном пространстве.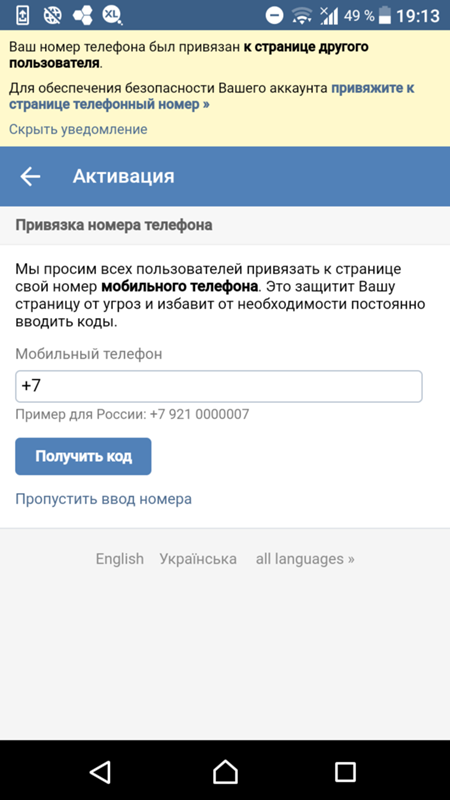 Интуитивно понятно, что связующее число представляет собой количество раз, которое каждая кривая оборачивается вокруг другой. Связующее число всегда является целым числом, но может быть положительным или отрицательным в зависимости от ориентации двух кривых.
Интуитивно понятно, что связующее число представляет собой количество раз, которое каждая кривая оборачивается вокруг другой. Связующее число всегда является целым числом, но может быть положительным или отрицательным в зависимости от ориентации двух кривых.
Число зацепления было введено Гауссом в виде интеграла зацепления . Это важный объект изучения в теории узлов, алгебраической топологии и дифференциальной геометрии, и он имеет множество приложений в математике и естественных науках, включая квантовую механику, электромагнетизм и изучение сверхспирализации ДНК.
Содержание
- 1 Определение
- 2 Расчет номера соединения
- 3 Свойства и примеры
- 4 Определение интеграла Гаусса
- 5 Обобщения
- 6 Примечания
- 7 См. также
- 8 Каталожные номера
Определение
Любые две замкнутые кривые в пространстве можно переместить ровно в одно из следующих стандартных положений. Это определяет номер ссылки:
Это определяет номер ссылки:
| ⋯ {\ Displaystyle \ cdots} | Файл: Номер ссылки -2.svg | Файл: Номер ссылки -1.svg | Файл: Номер ссылки 0.svg | ||
| номер привязки -2 | номер привязки -1 | номер привязки 0 | |||
| Файл:Linking Number 1.svg | Файл:Linking Number 2.svg | Файл:Linking Number 3.svg | ⋯{\ Displaystyle \ cdots} | ||
| связывание №1 | связывание номер 2 | связывание №3 |
Каждая кривая может проходить сама через себя во время этого движения, но две кривые должны оставаться разделенными.
Вычисление числа связей
Файл:Linking Number Example.svg
С шестью положительными пересечениями и двумя отрицательными пересечениями эти кривые имеют связующее число два.
Существует алгоритм для вычисления числа связей двух кривых из диаграммы связей. Пометьте каждое пересечение как положительное или отрицательное в соответствии со следующим правилом [1] :
Общее количество положительных пересечений минус общее количество отрицательных пересечений равно , удвоенному номеру связи. То есть:
- номер связи = n1 + n2-n3-n42 {\ displaystyle {\ mbox {номер связи}} = {\ frac {n_ {1} + n_ {2} -n_ {3} -n_ {4}} { 2}}}
, где N 1 , N 2 , N 3 , N 4 представляют количество перекрестных соотношений каждого из четырех типов. Две суммы n1 + n3 {\ displaystyle n_ {1} + n_ {3} \, \!} и n2 + n4 {\ displaystyle n_ {2} + n_ {4} \, \!} всегда равны, [ 2] , что приводит к следующей альтернативной формуле
- номер связи = n1−n4 = n2−n3.
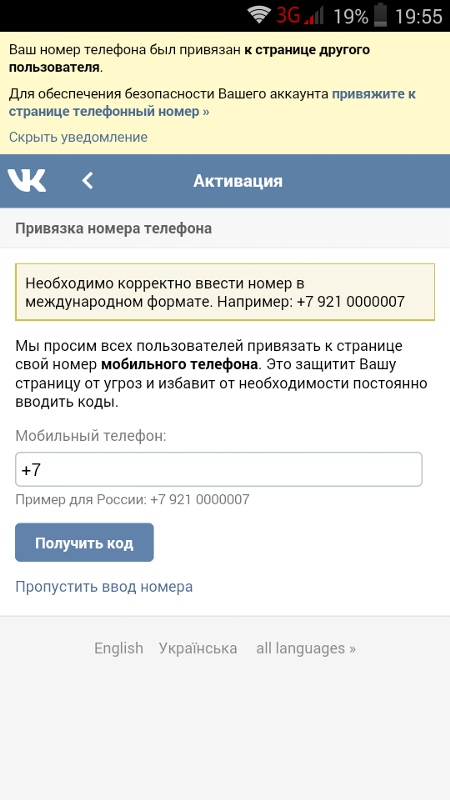 {\ displaystyle {\ mbox {номер связи}} \, = \, n_ {1} -n_ {4} \, = \, n_ {2} -n_ {3}.}
{\ displaystyle {\ mbox {номер связи}} \, = \, n_ {1} -n_ {4} \, = \, n_ {2} -n_ {3}.}
Обратите внимание, что n1−n4{\displaystyle n_{1}-n_{4}} включает только точки пересечения синей кривой красной, а n2−n3{\displaystyle n_{2}-n_{3}} включает только перекрёстки.
Свойства и примеры
Файл:Labeled Whitehead Link.svg
Две кривые связи Уайтхеда имеют нулевой номер связи.
- Любые две несвязанные кривые имеют нулевой связующий номер. Однако две кривые с нулевым номером связи все еще могут быть связаны (например, связь Уайтхеда).
- Изменение ориентации любой из кривых на противоположное отменяет номер связи, в то время как изменение ориентации обеих кривых оставляет его неизменным.
- Номер связи является хиральным: получение зеркального отображения ссылки отрицает номер связи. Наше соглашение о положительном числе связей основано на правиле правой руки.
- Число витков ориентированной кривой в плоскости x — y равно ее номеру связи с осью z (думая о z -ось как замкнутая кривая в 3-сфере).
 {3}}, определите Карта Гаусса Γ{\ displaystyle \ Gamma} из тора в сферу с помощью
{3}}, определите Карта Гаусса Γ{\ displaystyle \ Gamma} из тора в сферу с помощью- Γ (s, t) = γ1 (s) −γ2 (t) | γ1 (s) −γ2 (t) |. {\ displaystyle \ Gamma (s, t) = {\ frac {\ gamma _ { 1}(s)-\gamma _{2}(t)}{|\gamma _{1}(s)-\gamma _{2}(t)|}}.}
Выберите точку в единичная сфера, v , так что ортогональная проекция звена на плоскость, перпендикулярную v , дает диаграмму звеньев. Обратите внимание, что точка (s, t) , которая соответствует v по карте Гаусса, соответствует пересечению на диаграмме связи, где γ1{\displaystyle \gamma _{1}} находится над γ2{\displaystyle \gamma _ {2}}. Кроме того, район (s,t) отображается под картой Гаусса в окрестности v , сохраняя или меняя ориентацию в зависимости от знака пересечения. Таким образом, чтобы вычислить число зацеплений диаграммы, соответствующей v , достаточно подсчитать знаковых раз, когда карта Гаусса покрывает v . Поскольку v является регулярным значением, это в точности степень отображения Гаусса (т.
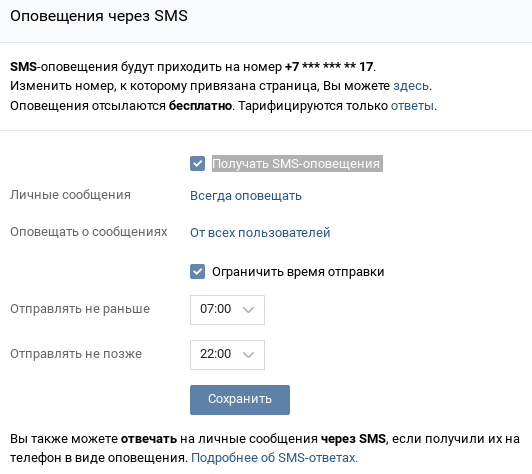 е. число раз со знаком, которое образ Γ покрывает сферу). Изотопическая инвариантность числа зацепления получается автоматически, поскольку степень инвариантна относительно гомотопических отображений. Любое другое обычное значение даст тот же номер, поэтому номер ссылки не зависит от какой-либо конкретной схемы связи.
9{3}}}\cdot (d\mathbf {r} _{1}\times d\mathbf {r} _{2}).}
е. число раз со знаком, которое образ Γ покрывает сферу). Изотопическая инвариантность числа зацепления получается автоматически, поскольку степень инвариантна относительно гомотопических отображений. Любое другое обычное значение даст тот же номер, поэтому номер ссылки не зависит от какой-либо конкретной схемы связи.
9{3}}}\cdot (d\mathbf {r} _{1}\times d\mathbf {r} _{2}).}Этот интеграл вычисляет общую площадь изображения карты Гаусса со знаком (интегральное выражение является якобианом Γ), а затем делится на площадь сферы (которая равна 4 π ).
Обобщения
- Точно так же, как замкнутые кривые могут быть связаны в трех измерениях, любые два замкнутых многообразия размерностей м и n могут быть связаны в евклидовом пространстве размерности m+n+1{\displaystyle m+n +1}. С любой такой связью связана карта Гаусса, степень которой является обобщением числа связи.
- Любой каркасный узел имеет число самосвязывания, полученное путем вычисления числа связывания узла C с новой кривой, полученной путем небольшого перемещения точек C вдоль векторов каркаса.
 Число самосвязывания, полученное путем перемещения по вертикали (вдоль рамки доски), известно как число самосвязывания Кауфмана .
Число самосвязывания, полученное путем перемещения по вертикали (вдоль рамки доски), известно как число самосвязывания Кауфмана .
Примечания
- ↑ Это та же самая маркировка, которая используется для вычисления изгиба узла, хотя в этом случае мы помечаем только те пересечения, которые включают обе кривые связи.
- ↑ Это следует из теоремы Жордана о кривой, если любая из кривых проста. Например, если синяя кривая простая, то n 1 + n 3 и n 2 + n 2 + n 1 4 представляют собой кривые, умноженные на числа, умноженные на кресты красного цвета. из области, ограниченной синей кривой.
См. также
- номер обмотки
- дифференциальная геометрия кривых
- ссылка (теория узлов)
- Инвариант Хопфа
- номер для поцелуев
Каталожные номера
- Шаблон: Springer
- Шаблон: Springer
[PDF] Gauss ‘Linking Number Revisited
- DOI: 10.
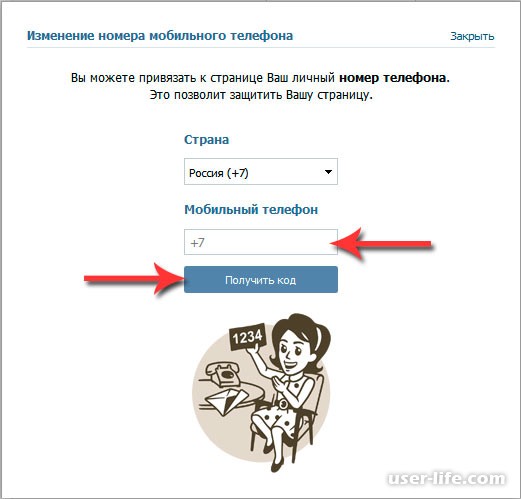 1142/S0218216511009261
1142/S0218216511009261 - CORPUS ID: 16640179
@ARTICLE. title={НОМЕР ССЫЛКИ GAUSS ПЕРЕСМОТРЕН}, автор = {Ренцо Л. Рикка и Бернардо Нипоти}, journal={Журнал теории узлов и ее разветвлений}, год = {2011}, объем = {20}, страницы={1325-1343} }- Р. Л. Рикка, Бернардо Нипоти
- Опубликовано 21 ноября 2011 г.
- Математика
- Журнал теории узлов и ее разветвлений
1833 г., предоставляя также альтернативное явное доказательство его современной интерпретации с точки зрения степени, подписанных пересечений и количества пересечений. Представленная здесь реконструкция полностью основана на тщательном изучении собственной работы Гаусса по земному магнетизму. Краткое обсуждение возможно независимого вывода, сделанного Максвеллом в 1867 г., завершает эту реконструкцию…
Просмотр через издателя
maths.ed.ac.ukДоказательство основанной на инвариантах формулы для числа связи и ее асимптотического поведения
В 1833 году Гаусс определил число связи двух непересекающихся кривых в трехмерном пространстве.
 Для открытых кривых этот двойной интеграл по параметризованным кривым является действительным и инвариантным по модулю жестких движений или…
Для открытых кривых этот двойной интеграл по параметризованным кривым является действительным и инвариантным по модулю жестких движений или…Полином Джонса для жидких узлов от спиральности
- Xin Liu, R. L. Ricca
Математика
- 2012
В этой статье мы доказываем, что в идеальных условиях спиральность жидких узлов, таких как вихревые нити или трубки магнитного потока, обеспечивает принципиально новые топологические средства, с помощью которых мы можем…
Формула для числа связи в Термины изометрических инвариантов отрезков прямых
Число зацепления обычно определяется как изотопический инвариант двух непересекающихся замкнутых кривых в трехмерном пространстве. Однако первоначальное определение 1833 года Гауссом в виде двойного…
О некоторых (мульти)симплектических аспектах инвариантов зацеплений
- Антонио Микеле Мити, М. Спера
Математика
- 2018
Wurzbacher and Zambon, RWZ), нарушающие стандартную гидродинамическую карту соимпульса Арнольда, Марсдена и Вайнштейна и…
Теория телесного угла Максвелла и построение заузленных полей
Мы даем систематическое описание функции телесного угла как средство построения заузленного поля для любой кривой или зацепления в .
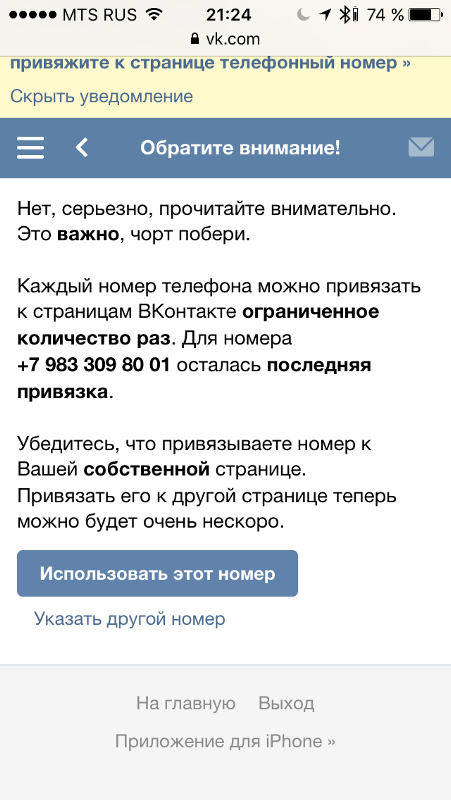 Это чисто геометрическая конструкция, в которой все…
Это чисто геометрическая конструкция, в которой все…ГИДРОДИНАМИЧЕСКАЯ ГОМОТОПИЧЕСКАЯ КАРТА КОИМПУЛЬСА И МУЛЬТИСИМПЛЕКТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ВЫСШИХ ЧИСЕЛ СВЯЗИ карта Арнольда, Марсдена, Вайнштейна и других…
Линкинг и теория Морса
- Дж. Асплунд
Математика
- 2014
В этой статье мы используем теорию Морса и градиентный поток функции Морса-Смейла для вычисления числа связей двухкомпонентной связи L в S3 путем подсчета знакового числа градиента…
Импульс вихревых клубков по взвешенной информации о площади.
- С. Цукчер, Р. Л. Рикка
Физика
Физический обзор. E
- 2019
Показан недавно представленный метод, основанный на геометрической интерпретации импульса вихревых линий, для определения динамических свойств сети узлов и звеньев, обеспечивающий мощный инструмент для диагностики вихревых нитей или другие сети нитевидных структур.

Обобщение лент и поворот решеткой ленты
- E. Dagrosa, A. Owczarek
Математика
- 2014
для стандартной канонической порибейны от дифференциации. и полный поворот ленты. Здесь мы приводим интегральное выражение,…
Спиральность, зацепление и изгиб в сферической геометрии
- Дж. Кэмпбелл, М. Бергер
Физика
- 2014
Связывающие числа, интегралы спиральности, скручивание и изгиб — все это описывает топологию и геометрию кривых и векторных полей. Однако топология пространства, в котором живут кривые и поля, может влиять…
Физика
- 1998
Кратко рассмотрена история взаимодействия физики и математики в теории узлов. В частности, исходное определение числа связи Гаусса в контексте…
Число связи Гаусса и принцип электромагнитной неопределенности
- А. Аштекар, Алехандро Коричи
Физика
- 1997 5 Показано, что существует точный смысл, в котором неопределенность Гейзенберга между потоками электрического и магнитного полей через конечные поверхности определяется (половина $\hbar$ раза) гауссовым…
- R.
 L. Ricca
L. Ricca Математика
Слушания Королевского общества A: Математические, физические и инженерные науки
- 2007
Topology Bounds Energy of Cools and Links
В этой бумаге, мы определяем два квадрата, 2007
В этой бумаге. геометрический и топологический характер, которые остались неопределенными в двух предыдущих результатах, полученных Арнольдом (Arnold 1974 In Proc. Summer School in Diff.…
ГЛАВА 11 – Геометрические аспекты в развитии теории узлов
- M. Epple
Mathematics
- 1999
Geometry of C˘ Alug˘ Areanu’s Theorem
- M. Dennis, J. Hannay
Mathematics
- 2005
A central result in пространственная геометрия замкнутых скрученных лент — это теорема Кэлугэряну (также известная как формула Уайта или теорема Кэлугэряну-Уайта-Фуллера). Это позволяет связать целое число…
Геометрия теоремы Кэлугэряну
- М. Деннис, Дж.
 Ханней
Ханней Математика
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences
- 2005
(также известная как формула Уайта или теорема Кэлугэряну – Уайта – Фуллера). Это позволяет целочисленное связывание…
Структурная сложность и динамические системы
- Р. Л. Рикка
Физика
- 2009
Этой статьей мы хотим отдать дань уважения 150-летнему опыту работы над топологической гидромеханикой. Для этого мы рассмотрим оригинальный вклад Гельмгольца (1858 г.) по топологическим вопросам, связанным с вихрем…
XI . Математическая теория магнетизма. Продолжение части I
65. В ходе некоторых исследований по обратным задачам о распределении магнетизма и по сравнению электромагнитов и обычных магнитов я нашел чрезвычайно удобным…
Бездивергентные поля: энергия и число асимптотических пересечений 2-форма co в трехмерном пространстве, которая является сохраняющейся величиной в том смысле, что она откатывается назад при эволюции во времени.
 В…
В…Обзор дифференциальной и симплектической геометрии зацепляющих чисел
- М. Спера
Математика
- 2006
Резюме. Цель настоящего обзора в основном состоит в том, чтобы проиллюстрировать некоторые недавно появившиеся дифференциальные и симплектические геометрические аспекты связывающих чисел обычного и высшего порядка…
ПОВЕРХНОСТЬ СВЯЗАННЫЙ НОМЕР | Вычисление секретов жизни: вклад математических наук в молекулярную биологию | The National Academies Press
Ниже приведен неисправленный машиночитаемый текст этой главы, предназначенный для обеспечения наших собственных поисковых систем и внешних систем очень богатыми, репрезентативными главами. текст каждой книги с возможностью поиска. Поскольку это НЕИСПРАВЛЕННЫЙ материал, рассмотрите следующий текст как полезный, но недостаточный заменитель для авторитетных страниц книги.
НАВИТАНИЕ ДВОЙНОЙ СПИРЛИ: С ИСПОЛЬЗОВАНИЕМ ГЕОМЕТРИИ, ТОПОЛОГИИ И МЕХАНИКИ ДНК 167
компоненты, которые имеют непосредственное отношение к поверхности и экспериментам, связанным с поверхностью.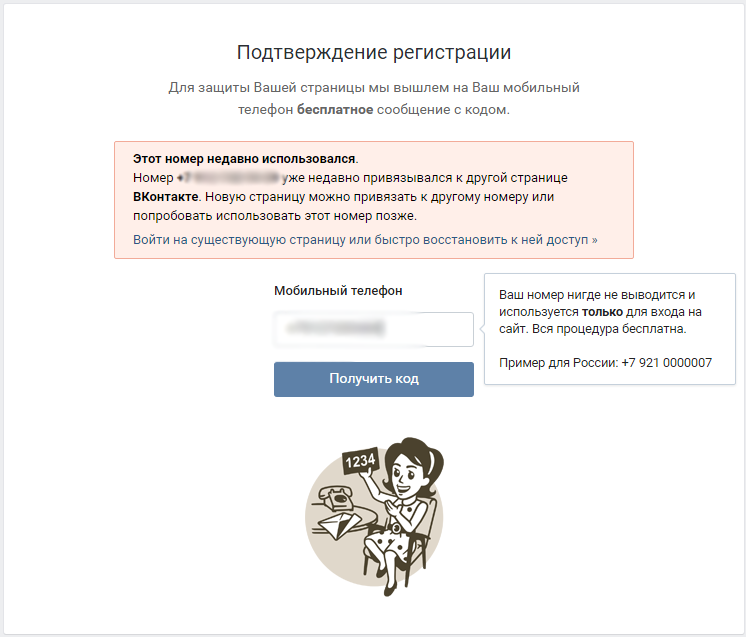 Связующий номер закрытого
ДНК, вынужденная лежать на поверхности, делится на две целые величины: число поверхностных связей, которое
измеряет намотку ДНК вокруг поверхности и число витков, которое является мерой
количество раз, когда позвоночник соприкасается с поверхностью или отрывается от нее (White et al., 1988). Экспериментально,
первое количество можно измерить с помощью рентгеновской дифракции, а второе можно измерить с помощью пищеварения или
методы следования. В частности, для нуклеосомы частичный вклад в число поверхностных связей, обусловленный
на левостороннюю обертку вокруг цилиндрического сердечника – 1,85 (Finch et al., 1981; Richmond et al., 1984).
Кроме того, число витков было измерено как число пар оснований ДНК на
нуклеосома делится примерно на 10,17 (Дрю и Трэверс, 1985).
НОМЕР СОЕДИНЕНИЯ ПОВЕРХНОСТЕЙ
Дадим теперь формальное определение двух величин, числа зацеплений поверхностей SLk и числа витков, для
замкнутая ДНК на поверхности белка.
Связующий номер закрытого
ДНК, вынужденная лежать на поверхности, делится на две целые величины: число поверхностных связей, которое
измеряет намотку ДНК вокруг поверхности и число витков, которое является мерой
количество раз, когда позвоночник соприкасается с поверхностью или отрывается от нее (White et al., 1988). Экспериментально,
первое количество можно измерить с помощью рентгеновской дифракции, а второе можно измерить с помощью пищеварения или
методы следования. В частности, для нуклеосомы частичный вклад в число поверхностных связей, обусловленный
на левостороннюю обертку вокруг цилиндрического сердечника – 1,85 (Finch et al., 1981; Richmond et al., 1984).
Кроме того, число витков было измерено как число пар оснований ДНК на
нуклеосома делится примерно на 10,17 (Дрю и Трэверс, 1985).
НОМЕР СОЕДИНЕНИЯ ПОВЕРХНОСТЕЙ
Дадим теперь формальное определение двух величин, числа зацеплений поверхностей SLk и числа витков, для
замкнутая ДНК на поверхности белка.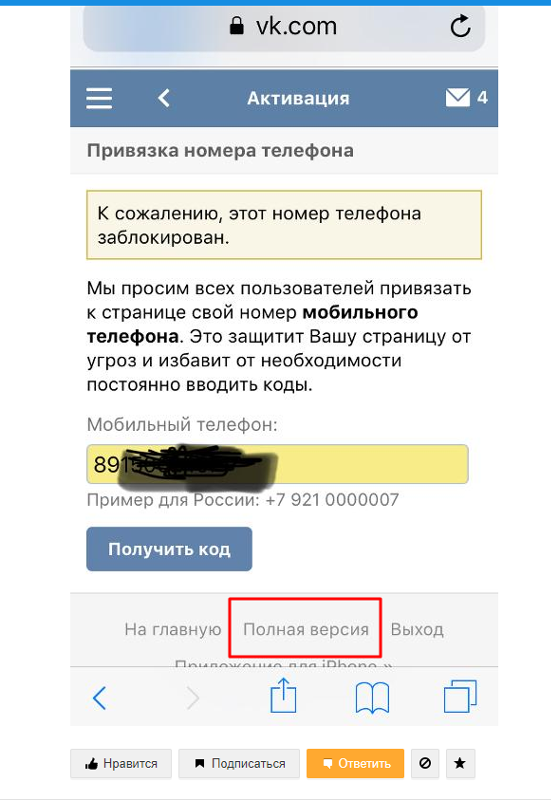 Предположим, что рассматриваемая поверхность обладает тем свойством, что в каждой точке вблизи
оси ДНК имеется хорошо выраженный вектор нормали к поверхности. Единичный вектор вдоль этого вектора будем обозначать
на v. (Мы предполагаем, что поверхности ориентируемы. В этом случае есть два возможных выбора для векторного поля
v в зависимости от стороны поверхности, на которую указывает векторное поле.) Если ось ДНК A смещена на небольшую
расстояние ε ˆ 0 вдоль этого векторного поля в каждой точке создается новая кривая Aε. ε следует выбирать достаточно малым, чтобы
что при смещении A на Aε не происходит пересечения одной кривой с другой. Кривая Aε также
замкнуты и могут быть ориентированы способом, совместимым с ориентацией A. Номер связи поверхности определяется
быть связующим числом исходной кривой A с кривой Aε (Уайт и Бауэр, 1988). Простые примеры
число поверхностных связей встречается для ДНК, оси которой лежат на плоских поверхностях или сфероидальных поверхностях. Во-первых, для
ДНК, ось которой лежит в плоскости, SLk = 0.
Предположим, что рассматриваемая поверхность обладает тем свойством, что в каждой точке вблизи
оси ДНК имеется хорошо выраженный вектор нормали к поверхности. Единичный вектор вдоль этого вектора будем обозначать
на v. (Мы предполагаем, что поверхности ориентируемы. В этом случае есть два возможных выбора для векторного поля
v в зависимости от стороны поверхности, на которую указывает векторное поле.) Если ось ДНК A смещена на небольшую
расстояние ε ˆ 0 вдоль этого векторного поля в каждой точке создается новая кривая Aε. ε следует выбирать достаточно малым, чтобы
что при смещении A на Aε не происходит пересечения одной кривой с другой. Кривая Aε также
замкнуты и могут быть ориентированы способом, совместимым с ориентацией A. Номер связи поверхности определяется
быть связующим числом исходной кривой A с кривой Aε (Уайт и Бауэр, 1988). Простые примеры
число поверхностных связей встречается для ДНК, оси которой лежат на плоских поверхностях или сфероидальных поверхностях. Во-первых, для
ДНК, ось которой лежит в плоскости, SLk = 0. Это легко увидеть, так как в этом случае векторное поле v является постоянным полем
перпендикулярно плоскости. Следовательно, кривая Aε целиком лежит по одну сторону от
Это легко увидеть, так как в этом случае векторное поле v является постоянным полем
перпендикулярно плоскости. Следовательно, кривая Aε целиком лежит по одну сторону от
НАВИТАНИЕ ДВОЙНОЙ СПИРЛИ: С ИСПОЛЬЗОВАНИЕМ ГЕОМЕТРИИ, ТОПОЛОГИИ И МЕХАНИКИ ДНК 168
плоскость и не может связать А, кривую, целиком лежащую на плоскости. Во-вторых, если ось ДНК лежит на круглой сфере,
SLk = 0. Чтобы убедиться в этом, мы можем считать без ограничения общности, что векторное поле v указывает на сферу. В этом
случай, когда смещенная кривая Aε полностью лежит внутри сферы и, следовательно, не может соединять A. Эти и дополнительные примеры
показаны на рис. 6.9..
SLk — это то, что технически называется дифференциальным топологическим инвариантом. Таким образом, SLk имеет три важных
характеристики. Во-первых, если комбинированная структура ДНК-ось-поверхность деформируется таким образом,
векторное поле v возникает в окрестности оси ДНК A, а сама A не нарушается, то остается SLk
инвариант. Например, если ДНК лежит в плоскости и эта плоскость деформирована, SLk остается равным 0; если он лежит на
деформированной сфере, SLk остается равным 0.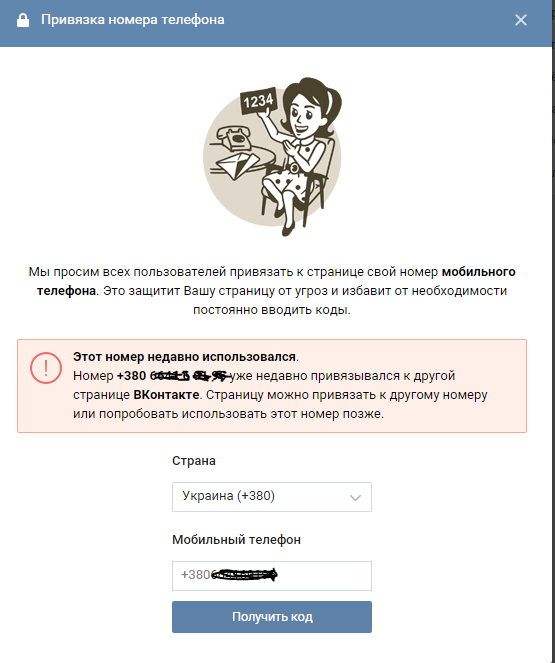 Таким образом, если ось ДНК лежит на поверхности любого типа сфероида,
SLк =0. Примеры сфероидов показаны на рис. 6.10а. Показан важный пример, когда SLk равен 0.
на рисунке 6.9г, в котором ось ДНК лежит на поверхности закрытого цилиндра. Второе важное свойство
SLk состоит в том, что он зависит только от поверхности вблизи оси. Следовательно, если поверхность, на которой лежит ось, сломана или
разрывается в местах, не близких к оси, SLk остается инвариантным. Например, если ДНК лежит на белке, а участок
белка не вблизи оси разрушается или распадается, SLk остается инвариантным. Третьим важным свойством является
что если ДНК лежит на поверхности и скользит по поверхности, то до тех пор, пока векторное поле v плавно изменяется от
точки на поверхности и до тех пор, пока в процессе скольжения ось не сломается, SLk остается инвариантной.
Таким образом, если цилиндр с крышкой на рис. 6.9d позволяли расширяться, а кривая оси должна была оставаться неизменной.
длины, он должен был бы разматываться, скользя по поверхности увеличенного цилиндра.
Таким образом, если ось ДНК лежит на поверхности любого типа сфероида,
SLк =0. Примеры сфероидов показаны на рис. 6.10а. Показан важный пример, когда SLk равен 0.
на рисунке 6.9г, в котором ось ДНК лежит на поверхности закрытого цилиндра. Второе важное свойство
SLk состоит в том, что он зависит только от поверхности вблизи оси. Следовательно, если поверхность, на которой лежит ось, сломана или
разрывается в местах, не близких к оси, SLk остается инвариантным. Например, если ДНК лежит на белке, а участок
белка не вблизи оси разрушается или распадается, SLk остается инвариантным. Третьим важным свойством является
что если ДНК лежит на поверхности и скользит по поверхности, то до тех пор, пока векторное поле v плавно изменяется от
точки на поверхности и до тех пор, пока в процессе скольжения ось не сломается, SLk остается инвариантной.
Таким образом, если цилиндр с крышкой на рис. 6.9d позволяли расширяться, а кривая оси должна была оставаться неизменной.
длины, он должен был бы разматываться, скользя по поверхности увеличенного цилиндра.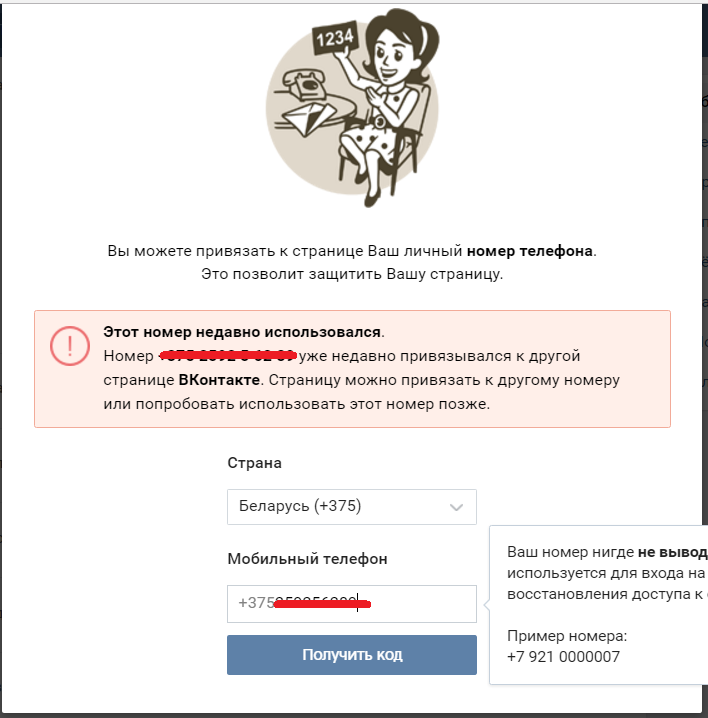 Однако SLk останется
равно 0.
Существует еще один класс биологически важных поверхностей, для которых ДНК может иметь SLk —
0. Это так называемые тороидальные поверхности. Они состоят из круглого кругового тора и их деформаций. Предполагать
осевая кривая A проходит всю длину круглой круглой ручки тора один раз, когда она оборачивает вокруг нее несколько
раз, н. Предположим далее, что внутренний радиус тора равен r. Для векторного поля v выберем
направленная внутрь поверхность нормальная. В этом случае, если выбрать ε = r, Aε будет центральной осью тора. Таким образом
SLk — номер связи кривой А с центральной осью
Однако SLk останется
равно 0.
Существует еще один класс биологически важных поверхностей, для которых ДНК может иметь SLk —
0. Это так называемые тороидальные поверхности. Они состоят из круглого кругового тора и их деформаций. Предполагать
осевая кривая A проходит всю длину круглой круглой ручки тора один раз, когда она оборачивает вокруг нее несколько
раз, н. Предположим далее, что внутренний радиус тора равен r. Для векторного поля v выберем
направленная внутрь поверхность нормальная. В этом случае, если выбрать ε = r, Aε будет центральной осью тора. Таким образом
SLk — номер связи кривой А с центральной осью
НАВИТАНИЕ ДВОЙНОЙ СПИРЛИ: С ИСПОЛЬЗОВАНИЕМ ГЕОМЕТРИИ, ТОПОЛОГИИ И МЕХАНИКИ ДНК 169
Рисунок 6.9
Примеры кривых перемещений и SLk. Для любой кривой A, лежащей на поверхности, формируется кривая перемещений Aε
путем перемещения на небольшое расстояние ε по нормали к поверхности в каждой точке кривой. Для плоских кривых, как в (а), все
векторы нормалей можно выбрать так, чтобы они указывали вверх, и тогда Aε находится выше A. Кривые не связаны между собой, и, следовательно, SLk
= 0. Для кривых на сферической поверхности, как в (b), векторы поверхности могут быть выбраны так, чтобы они указывали внутрь, и, следовательно, Aε равно
полностью внутри и, следовательно, не связывает A. SLk снова равно 0. В (c) и (d) векторы нормали к поверхности имеют
была выбрана направленной внутрь, а ε была установлена равной внутреннему радиусу поверхностей, на которые намотана ДНК.
В (c) Aε становится центральной осью тора, а SLk = +4. В (d) ДНК обернута плектонемически вокруг
закрытый цилиндр. Кривая смещения Aε целиком лежит внутри, поэтому SLk = 0.
Кривые не связаны между собой, и, следовательно, SLk
= 0. Для кривых на сферической поверхности, как в (b), векторы поверхности могут быть выбраны так, чтобы они указывали внутрь, и, следовательно, Aε равно
полностью внутри и, следовательно, не связывает A. SLk снова равно 0. В (c) и (d) векторы нормали к поверхности имеют
была выбрана направленной внутрь, а ε была установлена равной внутреннему радиусу поверхностей, на которые намотана ДНК.
В (c) Aε становится центральной осью тора, а SLk = +4. В (d) ДНК обернута плектонемически вокруг
закрытый цилиндр. Кривая смещения Aε целиком лежит внутри, поэтому SLk = 0.
НАВИТАНИЕ ДВОЙНОЙ СПИРЛИ: С ИСПОЛЬЗОВАНИЕМ ГЕОМЕТРИИ, ТОПОЛОГИИ И МЕХАНИКИ ДНК 170
тор. Отсюда следует, что если накрутка правая, то SLk = +n, а если накрутка левая, то
SLk = ân. В силу отмеченных выше инвариантных свойств SLk остается инвариантным даже при деформации круглого тора.
Примеры показаны на рисунке 6.10b.
Рисунок 6.10
(а) Деформации круглой сферы в сфероиды.