Шаблоны графиков функций: «Шаблон графиков функций» купить | ISBN 8593540100504

ИСПОЛЬЗОВАНИЕ ШАБЛОНОВ ПАРАБОЛ ДЛЯ ПОСТРОЕНИЯ ГРАФИКА ФУНКЦИИ у = а (х – т)2 + п

У р о к 14.
Использование шаблонов парабол
для построения графика функции у = а (х – т)² + п

Цель: продолжить формирование умения строить график функции у = а (х – т)² + п, используя при этом шаблоны парабол.

Ход урока

I. Организационный момент.

II. Устная работа.

Для каждого из графиков, изображенных на рисунке, найдите соответствующую функцию:

а) у = ; г) у = х² + 1;

б) у = –2х² + 1; д) у = ;

в) у = (х – 1)² – 2; е) у = (х + 1)² – 2.

III. Формирование умений и навыков.

Учащиеся выполняют з а д а н и я двух групп:

– построение графика функции у = а (х – т)² + п с использованием шаблонов;

– построение графика функции у = а (х – т)² + п с помощью преобразований.

Упражнения:

1-я г р у п п а.

1. № 107(а,г), № 112.

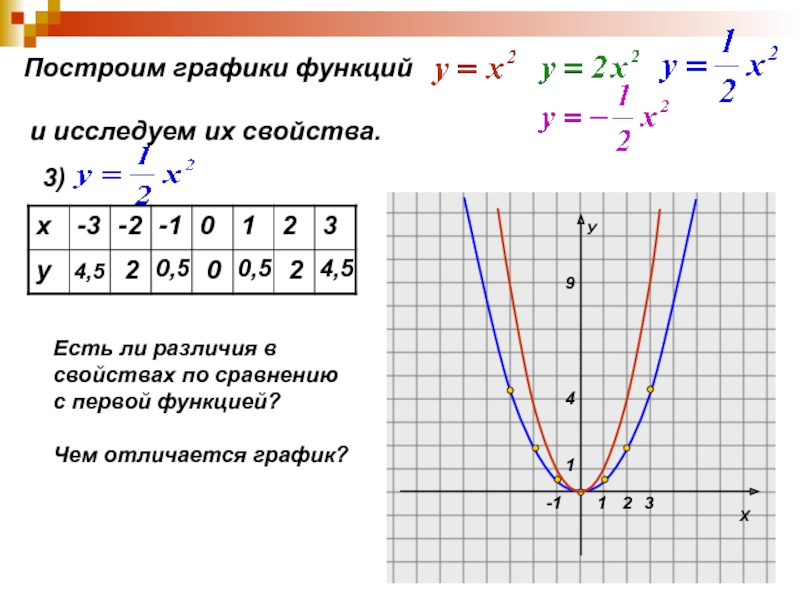
2. Используя шаблон параболы у = 2х², постройте график функций:

а) у = 2 (х + 1)² – 4; б) у = –2 (х – 3)² + 2.

3. Используя шаблон параболы у = х², постройте график функции:

а) у = ;

б) у = .

2-я г р у п п а.

1. Постройте графики функции:

а) у = ;

б) у = –3(х – 1)² + 4;

в) у =

2. Задайте формулой функцию, график которой изображен на рисунке:

IV. Проверочная работа.

В а р и а н т 1

1. Изобразите схематически графики функций:

а) у = –(х – 3)²;

б) у = х² + 1;

в) у = 2 (х + 1)² – 3.

2. Используя шаблон параболы у = х², постройте график функций:

а) у = (х + 2)² – 3;

б) у = –(х – 1)² + 4.

3*. Задайте формулой функцию, график которой изображен на рисунке:

В а р и а н т 2

1. Изобразите схематически графики функций:

а) у = –2х² + 3;

б) у = (х + 2)²;

в) у = –(х – 1)² – 2.

2. Используя шаблон параболы у = х², постройте графики функций:

а) у = (х – 3)² – 2;

б) у = –(х + 1)² + 5.

3*. Задайте формулой функцию, график которой изображен на рисунке:

V. Итоги урока.

В о п р о с ы у ч а щ и м с я:

– Что является графиком функции у = а (х – т)² + п?

– Как может быть получен график функции у = а (х – т)² + п из графика функции у = ах²?

– Какие координаты имеют вершины парабол:

у = 2 (х – 3)² + 4, у = (х + 1)² – 5?

Домашнее задание:

1. № 108, № 113.

2. Постройте графики функций:

а) у = –2 (х – 1)² + 3; б) у = (х + 2)² – 4.

В а р и а н т 1

1. Изобразите схематически графики функций:

а) у = –(х – 3)²;

б) у = х² + 1;

в) у = 2 (х + 1)² – 3.

2. Используя шаблон параболы у = х², постройте график функций:

а) у = (х + 2)² – 3;

б) у = –(х – 1)² + 4.

3*. Задайте формулой функцию, график которой изображен на рисунке:

В а р и а н т 2

1. Изобразите схематически графики функций:

а) у = –2х² + 3;

б) у = (х + 2)²;

в) у = –(х – 1)² – 2.

2. Используя шаблон параболы у = х², постройте графики функций:

а) у = (х – 3)² – 2;

б) у = –(х + 1)² + 5.

3*. Задайте формулой функцию, график которой изображен на рисунке:

НОУ ИНТУИТ | Лекция | Графика

< Лекция 2 || Лекция 3: 123456 || Лекция 4 >

Аннотация: В лекции представлены методы построения типичных графиков функций на плоскости и в пространстве, а также инструменты их редактирования, форматирования и настройки. Описаны разные технологические приемы построения графиков функций: автоматически, с помощью сетки и с применением специальных функций.

Ключевые слова: программа, координаты, панель инструментов, графика, меню, список, шаблон, прямоугольник, имя функции, курсор, область определения, функция, график, множества, значение, опция, радиус, массив

intuit.ru/2010/edi»>Цель лекции. Научить строить графики функций в разных системах координат с помощью различных технологических приемов. Показать способы форматирования и настройки разных типов графиков и диаграмм.

3.1. Инструменты графики

MathCAD предоставляет широкие возможности для построения графиков. Графические построения являются универсальными и легкими в использовании. Программа позволяет строить графики на плоскости и в трехмерном пространстве. Можно использовать декартовы и полярные координаты на плоскости, сферическую и цилиндрическую систему координат в пространстве.

Панель Математика содержит панель инструментов графики. Для построения графиков используются шаблоны. Большинство параметров графического процессора, необходимых для построения графиков, по умолчанию задается автоматически. Поэтому для начального построения графика того или иного вида достаточно задать тип графика. На панели Graph (Графика) или в меню Insert/ Graph (Вставка/Графика) содержится список из семи основных типов графиков.

Рис. 3.1.

Панель Графика

1. Декартов график [@] —шаблон двухмерного графика;
2. Полярный график [Ctrl+ 7] —шаблон графика в полярной системе координат;
3. График поверхности [Ctrl+ 2] — шаблон для построения трехмерного графика;
4. Карта линий уровня [Ctrl+ 5] —шаблон для контурного графика трехмерной поверхности;
5. 3D точечный график –шаблон для графика в виде точек в трехмерном пространстве;
6. 3D столбиковая гистограмма –шаблон для изображения в виде совокупности столбиков в трехмерном пространстве;
7. intuit.ru/2010/edi»>Векторное поле— создать шаблон для графика векторного поля на плоскости.

Для вывода шаблона двухмерной графики в декартовой системе координат служит кнопка декартов график на панели Graph [3, 8]. Она выводит в текущее положение курсора шаблон графиков в декартовых координатах (Рис.3.2). Незаполненный шаблон графика — пустой прямоугольник с шаблонами данных в виде темных маленьких прямоугольников, расположенных около осей абсцисс и ординат будущего графика.

Рис. 3.2. Шаблон графика в декартовых координатах

В средние шаблоны данных надо поместить имя функции F(x) оси абсцисс x. Если строятся графики нескольких функций в одном шаблоне, то для их разделения следует использовать запятые. Крайние шаблоны данных служат для указания предельных значений абсцисс и ординат, т. е. они задают масштабы графика. Если оставить эти шаблоны незаполненными, то масштабы по осям графика будут устанавливаться автоматически. Масштабы, могут оказаться неудобными для представления целиком всего графика в максимальном размере. Рекомендуется всегда вначале использовать автоматическое масштабирование, а затем изменять масштабы на более подходящие. Для построения графика достаточно вывести курсор за пределы графического объекта.

3.2. Построение графиков функций на плоскости

Для построения графика функции надо написать функцию, выбрать интервалы построения графика по оси X и Y и обозначить параметры графика. При этом следует учитывать область допустимых значений существования функции или область определения. Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл. График функции может быть представлен в различных системах координат. Наиболее употребительна прямоугольная координатная система – декартова. На плоскости применяют полярные системы координат, а в пространстве, наряду с декартовыми, цилиндрические и сферические системы координат.

3.2.1.Декартов график

Пример 3.1. Построить графики функций : , , . Функция не существует в точке . Но график строится и никаких дополнительных действий предпринимать не нужно. В отличие от построения графиков поверхности. Но эту проблему рассмотрим ниже.

Построение графика

Форматирование графика

Параметры изображения (цвет и толщина линий, координатная сетка, разметка осей, надписи на графиках и др.) можно изменить, вызвав команду меню Format/Graph/X-Y Plot (Формат/График/декартов график) или щелкнув дважды по полю графика. Появится окно Formatting Currently Selected X-Y Plot

(Форматирование выбранного графика), в котором устанавливаются настройки в соответствующих вкладках (Рис.3.7).

Рис. 3.7. Окно форматирования декартова графика

• Вкладка X-Y оси устанавливает для осей X и Y : тип шкалы: логарифмическая Log scale, цифровая Numbered), линии сетки (Grid Lines), Сетку автоматическую (Auto Grid) или режим задания количества меток (Number of Grid). Внизу устанавливается стиль вида осей (Axes Style)/
• Вкладка Traces устанавливает условные обозначения различных кривых графика.
• Вкладка Надпись (Labels) расположение надписей.

Установка границ на осях координат

MathCAD обеспечивает следующие возможности устанавливать границы на осях координат:

• Автоматически, с включенным режимом Авто масштаб (Autoscale)(см. закладка » X-Y Оси » ).
• Автоматически, с выключенным режимом Авто масштаб.
• Вручную, вводя границы непосредственно на графике.

При включенном режиме Авто масштаб MathCAD устанавливает границу на каждой оси соответствующей первому главному делению, выходящему за пределы значений данных

При выключенном режиме Авто масштаб MathCAD устанавливает границы на осях точно равными пределам данных.

Добавление горизонтальных и вертикальных линий

Чтобы добавить горизонтальную или вертикальную линию к графику:

• вызвать окно форматирования графика в декартовых координатах,
• в диалоговом окне Форматирование— закладка » X-Y Оси » ,
• intuit.ru/2010/edi»>щёлкнуть » Нанести риски » (для X-оси, или Y-оси). MathCAD показывает два дополнительных пустых поля на каждой оси, для которой включена опция » Нанести риски «,
• впечатать значение, для которого нужно провести линию,
• чтобы удалить линию, удалить это число или щёлкните на поле » Нанести риски «

Дальше >>

< Лекция 2 || Лекция 3: 123456 || Лекция 4 >

Шаблоны диаграмм Excel — Скачать бесплатно

PINE BI: Ultimate Excel Charting Add-in: вставляйте пользовательские диаграммы простым щелчком и другие инструменты построения диаграмм!

Excel также позволяет почти неограниченные настройки диаграмм, с помощью которых вы можете создавать множество расширенных типов диаграмм, которых нет в Excel. Ниже вы также найдете эти расширенные шаблоны диаграмм, доступные для скачивания.

Вы также найдете несколько шаблонов диаграмм, доступных для загрузки для стандартных диаграмм Excel.

Вместо этого щелкните здесь, если вам нужна информация о создании, сохранении и использовании шаблонов диаграмм в Excel.

Расширенные шаблоны диаграмм

Диаграмма шкалы

Также известна как: Диаграмма шкалы , Диаграмма спидометра

Описание: Таблицы шкалы используют стрелки для отображения информации в виде показаний на циферблате. Они часто используются при сравнении KPI или бизнес-результатов с заявленной целью.

Подробнее:  Учебное пособие по измерительной диаграмме

Скачать

Надстройка для построения калибровочных диаграмм

7 различных шаблонов калибровочных диаграмм. 5 предустановленных стилей. 9 цветовых палитр. Полностью настраиваемый.

Узнать больше

Диаграмма торнадо

Также известна как:

Диаграмма воронки продаж, диаграмма бабочки

Описание: Диаграмма торнадо представляет собой модифицированную версию гистограммы, в которой категории данных отображаются вертикально таким образом, который напоминает торнадо.

Узнайте больше: Учебное пособие по диаграмме Tornado

Скачать

График выгорания

Также известен как: Н/Д

Описание: Диаграммы выгорания представляют оставшуюся работу в зависимости от времени. Это полезно для прогнозирования, когда вся работа будет завершена.

Узнайте больше: Учебное пособие по диаграмме Burndown

Скачать

Ступенчатая диаграмма

Также известна как: Н/Д

Описание: Ступенчатая диаграмма — это линейная диаграмма, в которой вертикальные и горизонтальные линии соединяют точки данных в серии, создавая ступенчатую прогрессию.

Узнайте больше: Учебное пособие по пошаговой диаграмме

Скачать

Диаграмма термометра

Также известна как: Диаграмма целей

Описание: Диаграммы термометра показывают текущий процент выполнения задачи или цели относительно цели.

Узнайте больше: Учебное пособие по термометру

Скачать

Квадрантная диаграмма

Также известна как: Н/Д

Описание: Квадрантная диаграмма представляет собой точечную диаграмму с фоном, разделенным на четыре равные части, что позволяет классифицировать точки данных по четырем квадрантам

90 004 Узнать больше: Quadrant Tutorial

Скачать

Диаграмма Ogive

Также известна как: График совокупной частоты

Описание: Диаграммы Ogive — это графики, используемые в статистике для иллюстрации кумулятивных частот.

Узнайте больше: Учебное пособие по диаграмме Ogive

Скачать

Маркированная диаграмма

Также известна как: Маркированная диаграмма Стивена Фью. Альтернатива калибровочной диаграмме.

Подробнее: Учебное пособие по диаграммам

Скачать

Диаграмма Mekko

Также известна как: Диаграмма Marimekko, мозаика

Описание: Двухмерная диаграмма с накоплением, где ширина столбца обычно представляет относительный размер сегмента, а высота разбивает каждый сегмент.

Узнайте больше: Учебное пособие по диаграмме Mekko

Скачать

Кривая нормального распределения

Также известна как: Кривая Белла, Гауссова кривая, Диаграмма Белла

Описание: Симметричный график, иллюстрирующий тенденцию данных группироваться вокруг среднего значения.

Узнайте больше: Учебное пособие по кривой нормального распределения

Скачать

Диаграмма ствола и листа

Также известна как: Стеблограмма

Описание: Диаграмма, которая разбивает каждую точку данных на «стебель» (первые числа) и «листья» (обычно последняя цифра) для отображать частотное распределение набора данных.

Узнайте больше: Учебное пособие по стеблю и листу

Скачать

Полярный участок

Также известен как: Н/Д

Описание: Полярный график используется для определения точек в пространстве в так называемой полярной системе координат.

Узнайте больше: Учебное пособие по полярному графику

Скачать

Диаграмма Венна

Также известна как: Н/Д

Описание: Диаграмма Венна использует круги, чтобы показать отношения между наборами, где наборы имеют некоторые общие черты.

Узнайте больше: Учебное пособие по диаграмме Венна

Скачать

Панельная диаграмма

Также известна как: Н/Д

Описание: Панельные диаграммы — это диаграммы, содержащие несколько областей, каждая из которых отображает свой набор данных, а не все данные в одной области.

Узнайте больше: Учебное пособие по панельным диаграммам

Скачать

Временная диаграмма

Также известна как: Веховая диаграмма

Описание: Временные диаграммы используются для визуализации состояния проектов в хронологическом порядке.

Узнайте больше: Учебное пособие по временной шкале

Скачать

Диаграммы прогресса (гистограмма и круг)

Также известен как: Н/Д

Описание: Диаграммы прогресса используются для отображения прогресса в достижении цели.

Узнайте больше: Учебное пособие по графику прогресса

Скачать

Пирамида населения

Также известна как: Н/Д

Описание: Пирамиды населения используются для визуального отображения подмножеств внутри населения.

Узнайте больше: Учебное пособие по пирамиде населения

Скачать

Диаграмма процентного изменения/отклонения

Также известен как: Н/Д

Описание: Диаграмма процентного изменения/отклонения отображает вторичную информацию на гистограмме.

Узнайте больше: Учебное пособие по диаграмме процентного изменения/дисперсии

Скачать

Базовые шаблоны диаграмм Excel

Столбчатые диаграммы

Описание: Столбчатая диаграмма представляет собой визуализацию данных, в которой каждый элемент представлен прямоугольником, где величина значений определяет высоту прямоугольника.

Узнайте больше: Учебное пособие по гистограмме

Скачать

Гистограммы

Описание: Гистограмма представляет собой визуализацию данных, в которой каждый элемент представлен прямоугольником, где величина значений определяет ширину прямоугольника.

Узнайте больше: Учебное пособие по гистограмме

Скачать

Диаграммы с областями

Описание: Диаграмма с областями похожа на линейную диаграмму, за исключением того, что область под линией окрашена, чтобы подчеркнуть величину.

Узнайте больше: Учебное пособие по диаграмме с областями

Скачать

Линейные диаграммы

Описание: Линейная диаграмма — это график, который использует линии для соединения отдельных точек данных за временной интервал.

Узнайте больше: Учебное пособие по линейным диаграммам

Скачать

Диаграмма Парето

Описание: Диаграмма Парето представляет собой гибрид столбцовой и линейной диаграмм, отображающий относительную важность факторов в наборе данных.

Узнайте больше: Учебное пособие по диаграмме Парето

Скачать

Карта водопада

Также известна как: Схема моста, схема летающих кирпичей, схема каскада или карта Марио

Описание: Водопадная диаграмма наглядно показывает кумулятивное влияние последовательных положительных или отрицательных значений на конечный результат (например, различные статьи доходов и расходов на итоговую прибыльность).

Узнайте больше: Учебное пособие по диаграмме водопада

Скачать

Диаграмма воронки продаж

Описание: Диаграмма воронки продаж анализирует различные этапы процесса, обычно сортируя значения в порядке убывания (от наибольшего к наименьшему) таким образом, что визуально это выглядит как воронка — отсюда и название.

Узнайте больше: Учебное пособие по диаграмме воронки продаж

Скачать

Свечной график

Описание: Свечной график показывает цены открытия, максимума, минимума и закрытия актива за определенный период времени.

Узнайте больше: Учебное пособие по свечным графикам

Скачать

График функции

Ваш браузер либо не поддерживает Javascript, либо вы отключили его. Чтобы использовать Mentimeter, обязательно включите Javascript. Как включить Javascript?

Шаблоны/Образование/Математика

Этот шаблон Mentimeter можно использовать как продолжение после применения модуля «Понятие функции», но он также работает сам по себе. Шаблон уточняет, как функции могут быть визуализированы и поняты с помощью графического представления. Шаблон разработан в первую очередь как введение, но его также можно использовать в середине или в качестве подкрепления в конце тематического блока, связанного с линейными функциями.

Как пользоваться шаблоном

Ученикам нужны карандаши и бумага, чтобы ответить на некоторые вопросы презентации.

Ниже приведены некоторые идеи о том, как должны использоваться слайды, но не стесняйтесь использовать шаблон по своему усмотрению. В каждый раздел этой страницы включена цель и другая информация, которая может быть полезна вам как учителю. Общая идея относительно всех слайдов заключается в том, что учащиеся должны работать по модели «Думай, пари, делись» (TPS). При реализации TPS учащиеся должны сначала ответить на вопрос индивидуально, затем обсудить в парах (или группах по три человека), а затем обсудить в классе. В качестве заключительного замечания. Содержимое слайдов предназначено в первую очередь для развития понимания учащимися математических концепций, а не процедурного «ноу-хау». Поэтому обсуждения и вопросы учащихся являются центральной частью использования презентации, где ваш опыт как учителя играет центральную роль в прояснении неправильных представлений и ведении дискуссий в классе.

Теоретическая основа

Функция определяется как понятие порога. Это означает, что он преображает — однажды выученный, он открывает новые способы понимания концепции, и его невозможно забыть. Непонимание концепции функции помешает учащемуся в дальнейшем получить глубокое математическое понимание.

Студенты иногда делают концептуальные ошибки при интерпретации графических представлений функций. Чтобы по-настоящему правильно понять график, учащиеся могут извлечь выгоду из продуманного дизайна обучающего программного обеспечения в сочетании с более глубокими математическими знаниями. Таким образом, этот шаблон может облегчить понимание функций, представленных графами, но требует некоторых математических знаний, чтобы связать возможности обучения с содержанием шаблона и желаемыми результатами.

Слайд 1 — График функции: Познакомить с темой лекции. Например, вы могли бы упомянуть, что графическое представление функции занимает центральное место в математике.

Слайд 2. Общая информация: Сообщите учащимся о методологии TPS и о том, как они могут получить доступ к презентации.

Слайд 3 — Критерии успеха: Представьте «критерии успеха» для урока с проблемой, которая будет повторно рассмотрена и решена в конце урока. Идея здесь состоит в том, чтобы сделать обучение видимым, чтобы учащиеся могли сами убедиться, что они действительно чему-то научились.

Слайд 4. По мнению учащихся, график — это…: Пусть учащиеся индивидуально напишут, как они понимают понятие графика. Это может помочь прояснить возможные заблуждения.

Слайд 5. Куда бы вы хотели положить банан?: Учащиеся должны понять, что банан следует размещать в определенном положении в зависимости от соотношения между осью Y и осью X для разминки.

Слайд 6. Где бы вы хотели разместить арбуз?: Учащиеся получают еще одну возможность попрактиковаться в идее размещения арбуза в определенном положении в зависимости от соотношения между осью Y и осью X.

Слайд 7 — Где находится сокровище?: Мысль здесь состоит в том, чтобы вызвать чувство «ага» в понимании необходимости единого математического языка. В частности, точки в системе координат x-y задаются в виде (x, y) (а не (y, x)).

Слайд 8 – Где расположены точки?: Учащиеся получают возможность закрепить понимание (x,y)-представления с помощью точек.

Слайд 9 — Функциональная машина, которая принимает x:s и дает y:s: Это ключевой слайд. Слайд основан на предыдущем модуле («Концепция функции») и связывает «метафору-машину-функция» с графическим представлением.

Слайд 10. В какое значение преобразуются числа -4 и 2 с помощью функциональной машины?: Это ключевой слайд. Идея здесь состоит в том, чтобы укрепить интуицию из предыдущего слайда, в частности, что функция может быть представлена ​​и визуализирована с помощью графика.

Слайд 11: Какова функция машины?: Это ключевой слайд. Идея здесь состоит в том, чтобы усилить два предыдущих слайда, в частности, чтобы функцию можно было представить и визуализировать с помощью графика.

Слайд 12: Возьмите предыдущую функцию f(x)=0,5x+1 и вставьте x=1…: Идея здесь состоит в том, чтобы усилить связь между функцией и ее графиком. Идея здесь состоит в том, чтобы понять, что определенный ввод (по оси x) для функции дает определенный результат (f(x)=y по оси y) и что это справедливо для любого x.

Слайд 13: Наклон графика («подъем»/»разгон»): это ключевой слайд. Цель состоит в том, чтобы понять, что значение m относится к скорости изменения между x и y. Идея здесь состоит в том, чтобы получить концептуальное понимание, а не процедурное.

Слайд 14: Каков наклон этого графика?: Здесь понятие (рост/спад) усилено для лучшего понимания m-значения.

Слайд 15: Каков наклон двух графиков?: Здесь мы вводим отрицательный наклон. Идея здесь состоит в том, что учащийся получит представление о проблемах, связанных с применением концепции (подъем / бег) к отрицательному уклону.

Слайд 16: Каковы функции двух линий?: Применяя формулу (подъем/бег), учащийся должен быть в состоянии сформулировать функции.

Слайд 17: Формальное выражение линейной функции: «Введение» в формальное определение линейной функции. Попробуйте сообщить учащимся, что функция зависит только от одной переменной (x) и что m-значение и b-значение являются константами.

Слайд 18: Изменение значений m и b линейной функции: видео, показывающее, что происходит с функцией в визуальном представлении при изменении констант m и b.

Слайд 19: Напишите три точки пересечения по оси y для графиков: Идея здесь состоит в том, чтобы развить понимание значения b или, другими словами, точек пересечения по оси y.