Разное

Трапеция css: Геометрические фигуры на CSS / Хабр

21.08.1993

Содержание

Основные Фигуры — SVG | MDN

  • « Предыдущая статья
  • Следующая статья »

Существует несколько основных фигур, используемых в большинстве рисунков SVG. Назначение этих фигур вполне очевидно из их имён. Мы привели здесь некоторые атрибуты, определяющие положение и размер, но спецификация элемента, вероятно, содержит более точное и полное описание, вместе с другими свойствами, не описанными здесь. Однако, так как они используются в большинстве документов SVG, важно иметь некоторое представление о них.

Чтобы вставить форму, нужно создать элемент в документе. Разные элементы соответствуют разным формам и требуют разные атрибуты для описания размера и положения этих форм. Некоторые немного громоздки, поскольку могут быть созданы другими формами, но для удобства они все здесь приведены и способствуют сохранению документов SVG настолько короткими и читаемыми, насколько это возможно. Все основные формы показаны на изображении справа. Код для генерации выглядит как-то так:

<?xml version="1. 0" standalone="no"?>
<svg version="1.1" xmlns="http://www.w3.org/2000/svg">
  <rect x="10" y="10" stroke="black" fill="transparent" stroke-width="5"/>
  <rect x="60" y="10" rx="10" ry="10" stroke="black" fill="transparent" stroke-width="5"/>
  <circle cx="25" cy="75" r="20" stroke="red" fill="transparent" stroke-width="5"/>
  <ellipse cx="75" cy="75" rx="20" ry="5" stroke="red" fill="transparent" stroke-width="5"/>
  <line x1="10" x2="50" y1="110" y2="150" stroke="orange" fill="transparent" stroke-width="5"/>
  <polyline points="60 110 65 120 70 115 75 130 80 125 85 140 90 135 95 150 100 145"
      stroke="orange" fill="transparent" stroke-width="5"/>
  <polygon points="50 160 55 180 70 180 60 190 65 205 50 195 35 205 40 190 30 180 45 180"
      stroke="green" fill="transparent" stroke-width="5"/>
  <path d="M20,230 Q40,205 50,230 T90,230" fill="none" stroke="blue" stroke-width="5"/>
</svg>

Примечание: Замечание: Атрибуты stroke, stroke-width и fill описываются в руководстве далее.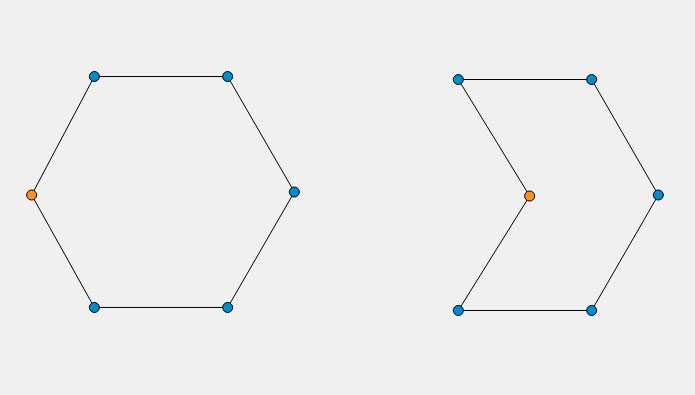

Прямоугольники

Элемент rect делает как раз то, что вы и ожидаете, то есть рисует прямоугольник на экране. Существуют только 6 основных атрибутов, которые контролируют положение и форму прямоугольника на экране. Ранее показанное изображение отображает два элемента rect, которые выглядят немного лишними. Один справа имеет набор атрибутов rx и ry, которые отвечают за округлые углы. Если этого набора нет, то по умолчанию они принимаются равными 0.

<rect x="10" y="10"/>
<rect x="60" y="10" rx="10" ry="10"/>
x

Положение x верхнего левого угла прямоугольника.

y

Положение y верхнего левого угла прямоугольника.

width

Ширина прямоугольника

height

Высота прямоугольника

rx

Радиус x углов прямоугольника

ry

Радиус y углов прямоугольника

Окружность

Как вы могли предположить, элемент circle рисует окружность на экране. Существует 3 атрибута для описания этого элемента.

<circle cx="25" cy="75" r="20"/>
r

Радиус окружности.

cx

Положение x центра окружности.

cy

Положение y центра окружности.

Эллипс

Ellipse — это наиболее общая форма элемента окружность, в котором можно масштабировать радиусы x и y (обычно называемые математиками половиной большой оси и половиной малой оси) окружности по отдельности.

<ellipse cx="75" cy="75" rx="20" ry="5"/>
rx

Радиус x эллипса.

ry

Радиус y эллипса.

cx

Положение x центра эллипса.

cy

Положение y центра эллипса.

Линия

Line изображает простую прямую линию. Её атрибутами являются две точки, которые определяют начальную и конечную точки линии.

<line x1="10" x2="50" y1="110" y2="150"/>
x1

Положение x точки 1.

y1

Положение y точки 1.

x2

Положение x точки 2.

y2

Положение y точки 2.

Ломаная линия

Элемент polyline воспроизводит группу соединённых прямых линий. Поскольку этот список может быть довольно длинным, все точки включены в один атрибут:

<polyline points="60 110, 65 120, 70 115, 75 130, 80 125, 85 140, 90 135, 95 150, 100 145"/>
точки

Список точек, каждая разделённая пробелом, запятой, EOL, или символом перевода строки. Каждая точка должна содержать два числа, координату x и координату y. Поэтому список (0,0), (1,1) и (2,2) может быть записан: «0 0, 1 1, 2 2».

Многоугольник

Элемент polygon очень похож на элемент polyline в том, что они образованы сегментами прямых линий, соединяющими список точек. Но для многоугольников путь автоматически возвращается к первой точке в конце, создавая тем самым замкнутую форму. Следует отметить, что прямоугольник является частным случаем многоугольника, поэтому polygon можно использовать для создания элемента <rect/> в случаях, когда необходимо большая гибкость.

<polygon points="50 160, 55 180, 70 180, 60 190, 65 205, 50 195, 35 205, 40 190, 30 180, 45 180"/>
точки

Список точек, каждая разделённая пробелом, запятой, EOL, или символом перевода строки. Каждая точка должна содержать два числа, координату x и координату y. Поэтому список (0,0), (1,1) и (2,2) может быть записан как: «0 0, 1 1, 2 2». Полигон замыкается финальной прямой линией от (2,2) до (0,0).

Путь

Path, вероятно, наиболее общая форма, которую можно использовать в SVG. Используя элемент path вы можете рисовать прямоугольники (с закруглёнными углами или без), окружности, эллипсы, ломанные линии и многоугольники; и по существу любые другие типы форм: кривые Безье, квадратические кривые и многое другое. По этой причине элемент path будет рассмотрен отдельно в следующей секции этого руководства, но сейчас отметим только, что существует единственный атрибут для контроля его формы.

<path d="M 20 230 Q 40 205, 50 230 T 90230"/>
d

Список точек и другой информации о том, как рисовать путь. Для подробной информации смотри секцию Пути.

  • « Предыдущая статья
  • Следующая статья »

Last modified: , by MDN contributors

Угол трапеции с помощью онлайн-калькулятора, формулы и примеры

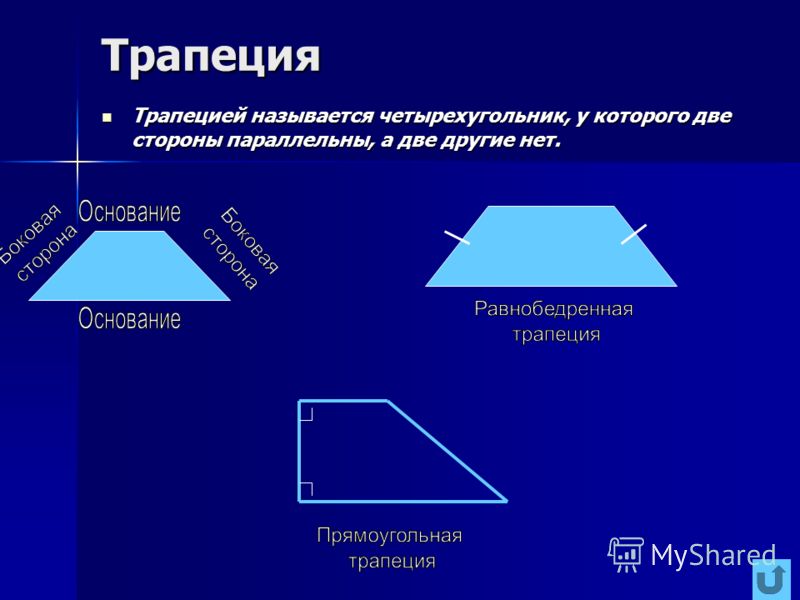
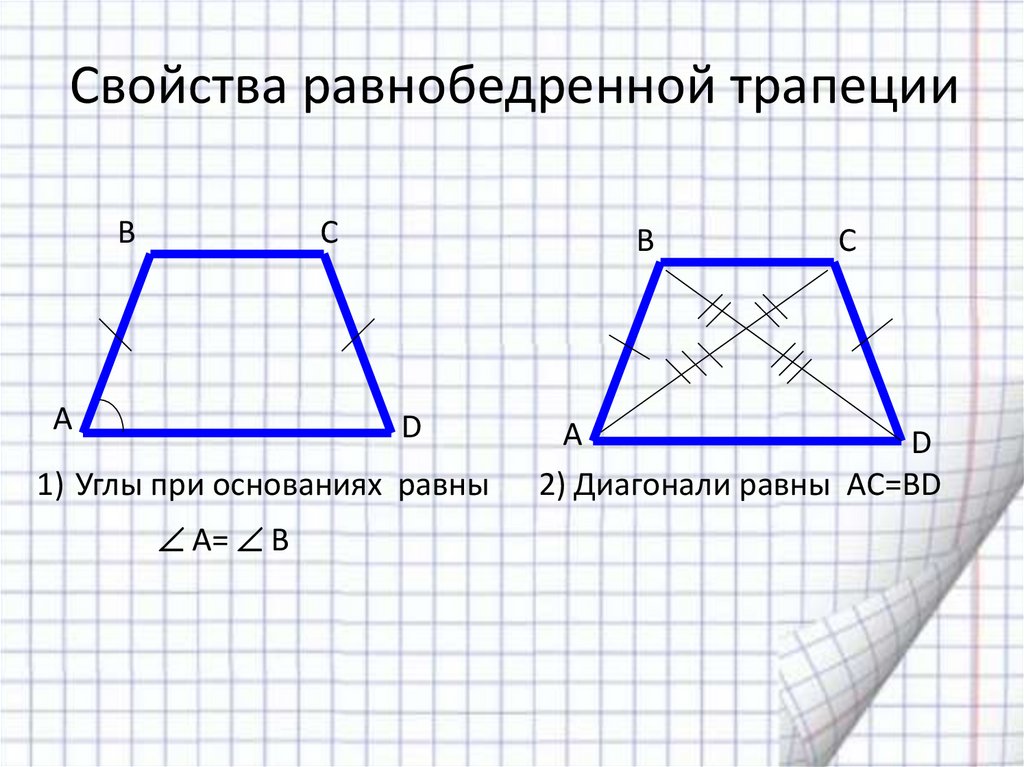
Трапеция —  геометрическая фигура представляет собой выпуклый четырехугольник с параллельными противоположными сторонами. Они называются основаниями. Две другие стороны — боковые. Трапеция, у которой они одинакового размера, называется равнобедренной. Если одна из боковых сторон образует у основания угол в 90 градусов-прямоугольной.

Прямая линия, проведенная от одного основания к другому, именуется высотой трапеции. Величина ее высчитывается делением суммы оснований на 2.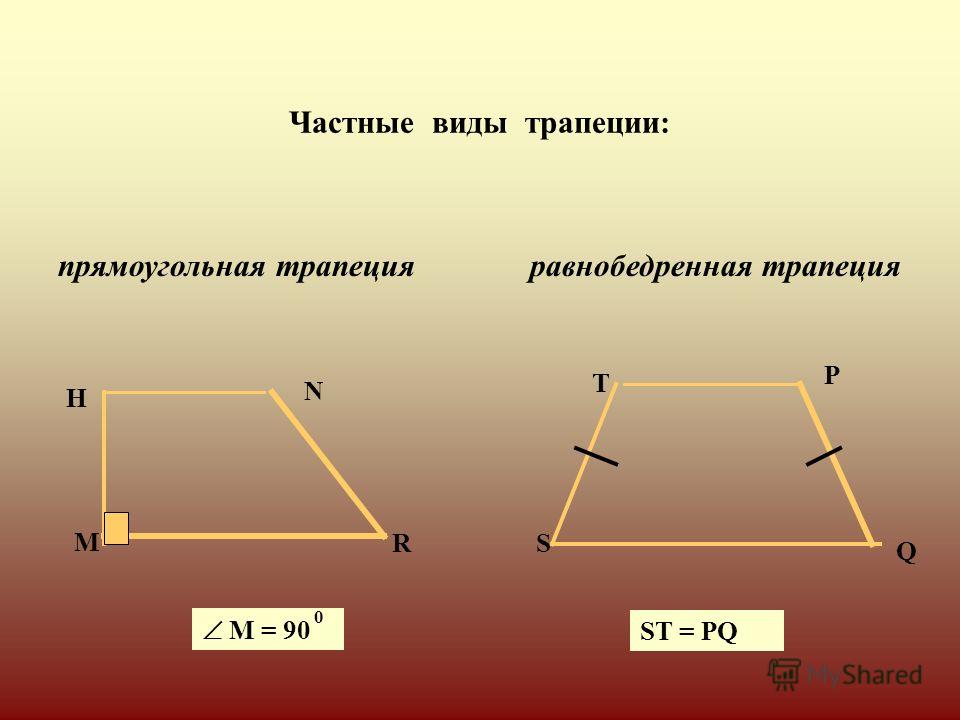 Диагонали — это отрезки, соединяющие противоположные углы фигуры. У равнобедренной трапеции они равны по длине. Средняя линия-прямая, делящая пополам боковые стороны.

  • Угол трапеции при основании через высоту и прилегающую боковую сторону
  • Угол трапеции через нижнее основание, боковую сторону и диагональ
  • Угол равнобедренной трапеции через нижнее основание, среднию линию и боковую сторону
  • Угол равнобедренной трапеции через среднию линию, верхнее основание и боковую сторону
  • Острый угол при нижнем основании прямоугольной трапеции через высоту и два основания
  • Острый угол при нижнем основании прямоугольной трапеции через два основания и боковую сторону

Угол трапеции при основании через высоту и прилегающую боковую сторону

Введем обозначения: h-высота, с — боковая сторона. Угол трапеции α при основании вычисляется с помощью формулы

sin α = h/с

где: h — высота трапеции, c — боковая сторона.

Высота (h):

ммсмдмм

Сторона (c):

ммсмдмм

Цифр после запятой:

012345678910Результат в: градусыcosрадианы

Пример. Заменим буквенные обозначения условными цифрами. Пример: если высота равна 9см, боковая сторона-11см, получим: sin α = 9 / 11 = 0,818 , отсюда α = 55º. Указанное значение находим в таблице синусов. Данный показатель синуса угла соответствует величине 55 градусов.

Через нижнее основание, среднию линию и боковую сторону в равнобедренной трапеции

Угол равнобедренной трапеции через нижнее основание, среднюю линию и боковую сторону находится по формуле:

cos α = (2a-2m) / 2c

где а — нижнее основание, m — средняя линия, с — боковая сторона.

Основание (a):

ммсмдмм

Ср.линия (m):

ммсмдмм

Сторона (c):

ммсмдмм

Цифр после запятой:

012345678910Результат в: градусыsinрадианы

Пример.Заменим буквы условными цифровыми значениями. Если нижнее основание равно 8 см, средняя линия-6, а боковая сторона-4,8 см, то косинус угла равен 0,41666, что соответствует 65 градусам. cos α = (2 * 8 — 2 * 6) / 2 * 4,8 = 0, 41666, отсюда α = 65º. Равнобедренная трапеция — геометрическая фигура с нижними острыми углами. Это ее особенность.

Угол трапеции, зная размер нижнего основания, боковой стороны и диагонали

Если известны эти величины, воспользуемся формулой:

cos α= (a²+c²-d²) / 2ac

где а-нижнее основание, d-диагональ, с-боковая сторона.

Основание (a):

ммсмдмм

Сторона (c):

ммсмдмм

Диагональ (d):

ммсмдмм

Цифр после запятой:

012345678910Результат в: градусыcosрадианы

Пример. При условной величине нижнего основания 4 см, диагонали — 5.7 см, боковой стороны — 4,4 см косинус равняется 0,081534, что соответствует углу 85 градусов по таблице функций. cos α= (4² + 4,4² — 5,7²) / 2*4*4,4 = 0,081534, отсюда α = 85º.

Через среднюю линию, верхнее основание и боковую сторону в равнобедренной трапеции

Нахождение угла равнобедренной трапеции через среднюю линию, верхнее основание и боковую сторону выполняется по предложенной формуле:

cos α = (2m-2b) / 2c

где m — средняя линия, b — верхнее основание, c — боковая сторона.

Ср.линия (m):

ммсмдмм

Основание (b):

ммсмдмм

Сторона (c):

ммсмдмм

Цифр после запятой:

012345678910Результат в: градусырадианыsin

Пример. Введем условные цифровые значения. Допустим, что у равнобедренной трапеции верхнее основание равно 4 см, средняя линия-6, боковая сторона-4 см. Косинус составляет 0,5. Значение соответствует 60 градусам по таблице Брадиса. cos α = (2 * 6 — 2 * 4) / 2 * 4 = 0,5, отсюда α = 60º

Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой стороны в прямоугольной трапеции

Находится по формуле

cos α = (a — b) / c

где a,b — основания, c — боковая сторона.

Н.основание (a):

ммсмдмм

В. основание (b):

ммсмдмм

Сторона (c):

ммсмдмм

Цифр после запятой:

012345678910Результат в: градусыsinрадианы

Пример. Если буквенные выражения заменить условными цифровыми, получится наглядный пример вычисления. Допустим, длина нижнего основания а 8 см, верхнего b-5,8 см, размер боковой стороны с-4,8. Подставив в формулу цифровые значения, получим итог: косинус равен 0,45833. Сравниваем показатель с таблицей вычисления Брадиса: он соответствует углу 63 градуса. cos α=(8 — 5,8) / 4,8 = 0,45833, отсюда α = 63º

Острый угол при нижнем основании, зная высоту и размеры двух оснований прямоугольной трапеции

При известных указанных величинах воспользуемся следующей формулой:

tg(α) = h / (a-b)

где h — высота, a,b — верхнее и нижнее основания.

Высота (h):

ммсмдмм

Н. основание (a):

ммсмдмм

В.основание (b):

ммсмдмм

Цифр после запятой:

012345678910Результат в: градусыsinрадианы

Пример. Введя условные цифровые значения h = 15, a = 11, b = 10 получим tg(α) = 15 / (11-10) = 15. При вычислении получим значение тангенса: 15. По таблице функций показатель соответствует 86 градусам.

Следует знать несколько закономерностей данной геометрической конструкции. У трапеции четыре угла, общая сумма которых составляет 360 градусов.

Равнобедренная отличается двумя равными острыми, прилегающими к нижнему основанию, и тупыми одинаковой величины-к верхнему. У прямоугольной трапеции два угла по 90 градусов, другие — острый и тупой. Если он прилегает к нижнему основанию, величина такого угла определяется делением высоты на разность между нижним и верхним основаниями.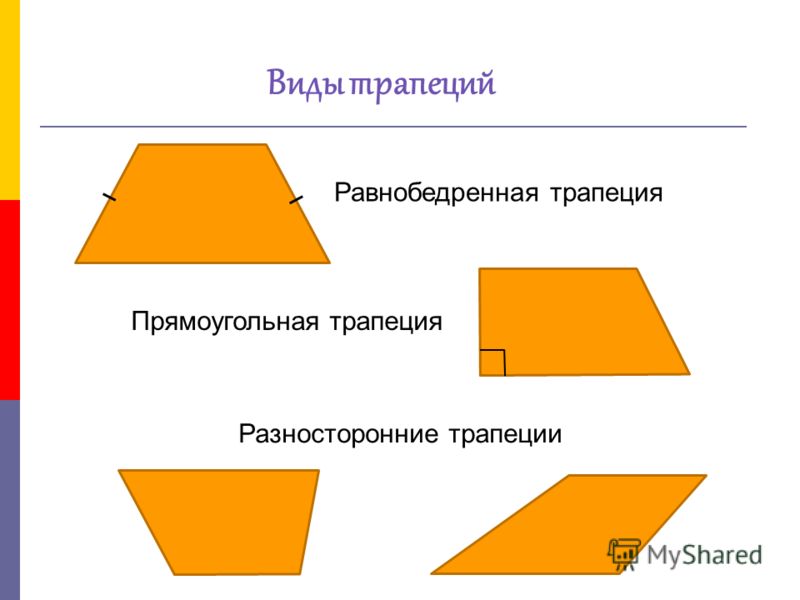 Угол трапеции при основании равен отношению высоты к боковой стороне.

html — Трапециевидная кнопка CSS со сплошной рамкой

Попробуйте следующий код:

ВАРИАНТ 1: ЧИСТЫЙ CSS

Логика этого подхода заключается в добавлении толстой нижней и толстой прозрачной правой границы для достижения эффект вкладки;

  • ПЛЮСЫ: очень минималистичный стиль и очень простой для понимания.
  • МИНУСЫ: очень ограничены в плане настройки (т.е. нельзя добавить границу на вкладку)
 .табы {
  дисплей: гибкий;
  flex-направление: строка;
}

.tab {
    высота: 0;
    ширина: 120 пикселей;
    нижняя граница: 50 пикселей сплошная #CCCCCC;
    граница справа: 20px сплошная прозрачная;
    граница-верхний-левый-радиус: 5px;
    box-sizing: граница-коробка;
    дисплей: блок;
}

.tab: не (: первый ребенок) {
    поле слева: -10px;
    z-индекс: 0;
}

.tab .метка{
  отступ: 15 пикселей;
  выравнивание текста: по центру;
  цвет: #444444;
}

. актив {
  нижняя граница: 50px сплошная #444444;
  z-индекс: 10;
}
.активный .label{
  цвет: #ffffff;
} 
 <дел>

TAB 1


TAB 2


TAB 3

ВАРИАНТ 2: ИСПОЛЬЗОВАНИЕ SVG В КАЧЕСТВЕ ФОНА ВКЛАДКИ

Логика этого подхода заключается в использовании двух отдельных векторных изображений (svg) в качестве встроенного фонового изображения:

  • ПЛЮСЫ: широкие возможности настройки; можно добавить границу на вкладку, можно добавить градиент фон для вкладки.
  • МИНУСЫ: требуются базовые знания о svg.
 .табы {
  дисплей: гибкий;
  flex-направление: строка;
  переполнение: видимое;
  отступ слева: 15px;
}

.tab {
    высота: 0;
    ширина: 130 пикселей;
    высота: 38 пикселей;
    поле слева: -15px;
    z-индекс: -1;
    курсор: указатель;
    размер фона: содержит;
    фон: прозрачный URL ("данные: изображение/svg+xml;utf8, w3.org/2000/svg' width=\"121px\" height=\"38px\" viewBox =\"0 0 121 38\"><путь d=\"M0,786477689,37.3880765 L0.786477689,5 L0.786477689,5 C0.786477689,2.790861 2.57733869,1 4.78647769,1 L102.838012,1 L102.838012,1 C104.471746,1 105.941285,1.99354246 106.549997,3.50964209 L120.152151,37.3880765 L0 .786477689,37.3880765 Z\" stroke=\"#979797\" fill=\"#F0F0F0\">") без повтора;
}

.tab .метка{
  box-sizing: граница-коробка;
  отступ: 12px;
  выравнивание текста: по центру;
  цвет: #444444;
  шрифт: 13px arial, без засечек;
  ширина: 90%;
}

.актив {
  фон: прозрачный URL ("данные: изображение/svg+xml;utf8,<путь d=\"M0,786477689,37.3880765 L0.786477689,5 L0.786477689,5 C0.786477689,2.790861 2.57733869,1 4.78647769,1 L102.838012,1 L102.838012,1 C104.471746,1 105.941285,1.99354246 106.549997,3.50964209 L120.152151,37.3880765 L0 .786477689,37.3880765 Z\" stroke=\"#2D94B5\" fill=\"#2D94B5\">") без повтора;
  z-индекс: 10;
}
. активный .label{
  цвет: #ffffff;
} 
 <дел>

TAB 1


TAB 2


TAB 3


ВКЛАДКА 4

Если вы хотите изменить цвета фона (заливки) и границы (обводки), просто проанализируйте класс .tab и .active , найдите свойство background и найдите/отредактируйте следующее во встроенном svg :

  • для обычной вкладки: штрих=\"#979797\" fill=\"#F0F0F0\"
  • для активной вкладки: штрих=\"#2D94B5\" fill=\"#2D94B5\"

Надеюсь, это поможет вам

4

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

трапециевидных фигур CSS, нарисованных на чистом CSS (и треугольников) – clubmate.

fi

трапециевидных фигур CSS, нарисованных на чистом CSS (и треугольников) формы трапеций, нарисованные на чистом CSS.

Они очень похожи на треугольники CSS, в основном это вытянутые треугольники… с большим количеством углов.

Треугольники CSS

Вот напоминание о треугольниках CSS, они работают, злоупотребляя значениями ширины границы в сочетании с размерами элемента.

903 90303
Shape Name
Arrow up
Arrow down
Arrow left
Стрелка вправо
Стрелка вправо
Стрелка вниз
Стрелка влево
влево
. :

 <дел>
<дел>
<дел>
<дел>
<дел>
<дел>
<дел>
<дел>

И стили треугольника:

 . arrow {
  отображение: встроенный блок;
  высота: 0;
  поле справа: 10px;
  ширина: 0;
}
.стрелка вверх {
  нижняя граница: сплошной черный цвет 15 пикселей;
  граница слева: 10px сплошная прозрачная;
  граница справа: 10px сплошная прозрачная;
}
.стрелка-вниз {
  граница слева: 10px сплошная прозрачная;
  граница справа: 10px сплошная прозрачная;
  граница сверху: сплошной черный цвет 15 пикселей;
}
.стрелка-вправо {
  нижняя граница: 10px сплошная прозрачная;
  граница слева: сплошной черный 15 пикселей;
  граница сверху: 10px сплошная прозрачная;
}
.стрелка-влево {
  нижняя граница: 10px сплошная прозрачная;
  граница справа: 15px сплошной черный;
  граница сверху: 10px сплошная прозрачная;
}
.стрелка-вверху справа {
  нижняя граница: 15px сплошная прозрачная;
  граница справа: 15px сплошной черный;
  border-top: 0 сплошной прозрачный;
}
.стрелка-вниз-вправо {
  нижняя граница: 0 сплошная прозрачная;
  граница справа: 15px сплошной черный;
  граница сверху: 15px сплошная прозрачная;
}
. стрелка-вниз-влево {
  нижняя граница: 0 сплошная прозрачная;
  граница слева: сплошной черный 15 пикселей;
  граница сверху: 15px сплошная прозрачная;
}
.стрелка-влево {
  нижняя граница: 15px сплошная прозрачная;
  граница слева: сплошной черный 15 пикселей;
  border-top: 0 сплошной прозрачный;
}

Трапеции CSS

Чтобы треугольники выглядели как трапеции, установите ширину на 100% (или другое подходящее значение) и поэкспериментируйте с шириной границ. Это то, что можно довольно легко извлечь в какую-то вспомогательную функцию трапеции.

А вот стили трапеций:

 .trapezoid {
 высота: 0;
 нижняя граница: 20px;
 ширина: 100%;
}
.трапеция вверх {
 нижняя граница: сплошной черный цвет 25 пикселей;
 граница слева: 20px сплошная прозрачная;
 граница справа: 20px сплошная прозрачная;
}
.трапеция-вниз {
 граница слева: 20px сплошная прозрачная;
 граница справа: 20px сплошная прозрачная;
 граница сверху: 25px сплошной черный;
}
.трапеция-справа {
 нижняя граница: сплошной черный цвет 25 пикселей;
 граница слева: 20px сплошная прозрачная;
 граница справа: 0 сплошной прозрачный;
 border-top: 0 сплошной прозрачный;
}
.
Добавить комментарий 
Ваш адрес email не будет опубликован. Обязательные поля помечены *
 
 
  
 © Орфографика.рф, 2010 - 2019
 Расшифровки, размещенные на сайте, предназначены только для личного, некоммерческого использования.
 При перепосте материалов обязательна активная ссылка: «Текст подготовлен компанией Орфографика.рф». 
Вопросы и предложения: info@орфографика.рф.