Полигон в графике: Полигональная графика. Что это такое, и как ее создавать

Полигональная графика. Что это такое, и как ее создавать

Дизайн и графика

24.11.201821.06.2022 от автора Медиасвод

Полигональные фигуры напоминают оригами или ограненные драгоценные камни. Давайте разберемся, что такое полигональная графика? И почему дизайнеры так любят использовать этот прием в своих работах?

Полигон (от греч. polýgonos – многоугольный), полигональная линия – это ломаная линия, составленная из конечного числа прямолинейных отрезков (звеньев). Под полигоном также понимают замкнутую ломаную линию, т. е. многоугольник.

Полигональная графика интеллектуальна

Это визуализация осознанной формы. Художникам и дизайнерам полигон помогает упростить, осмыслить, а значит, в дальнейшем правильно передать форму и объем объекта.

Помогает он и в трехмерной графике. Там полигон — это минимальная поверхность, элемент, из которого складываются каркасы  форм любой сложности.   Чем больше полигонов, тем более детализованной будет модель. В трехмерной графике в качестве полигонов обычно применяют треугольники.

Полигоны — простые, красивые, лаконичные и бесконечно многообразные вдохновляют многих современных дизайнеров. Из них можно составлять абстрактные композиции и стильные иллюстрации любой сложности

В этой статье вы узнаете много нового о полигонах и полигональной графике и увидите замечательные примеры ее использования. Также здесь собрано несколько уроков, которые помогут вам освоить эту технику.

Трехмерная графика. На этот вопрос нет однозначного ответа. Мастера 3D, предпочтут, несомненно, делать это в 3D max, Maya, или Cinema 4D. Последнее ПО настолько дружелюбно, что в нем может рисовать даже ребенок. В целом, полигональная графика достаточно проста в создании, особенно если сравнивать с фотореалистичной визуализацией. Она напоминает ранние дни компьютерного моделирования и анимации с налетом современных техник.  Чем меньше полигонов вы используете на стадии моделирования, тем более абстрактным будет результат. Для выраженного эффекта можно отключить функцию сглаживания в настройках рендеринга, и тогда вы получите четкие грани. Здесь все зависит от эффекта, которого вы хотите достичь. Использование низкополигональной техники совсем не означает, что сцена будет простой. Вы можете использовать сложные текстуры, реалистичные настройки отражений и преломлений в окружающей среде и т. д.

2D графика. Можно создавать полигональные шедевры в таких программах как Adobe Illustrator, CorelDraw и даже Adobe Photoshop. Эти программы, в отличие от специфичных 3D пакетов, хорошо знакомы большинству дизайнеров. Таким методом можно создавать стилизованные, декоративные изображения с потрясающими цветовыми сочетаниями.

А еще можно дополнять полигональную графику фотографиями, создавая удивительные коллажи, напоминающие дополненную реальность и намекающие о связях между реальным и виртуальными мирами. Некоторые работы дополняются типографикой.

А еще можно попробовать онлайн-генераторы полигонов

Trianglify

Очень простой генератор, который позволит создать низкополигональные фоны с заданной палитрой цветов. Можно создать красивый фон для Вашего дизайна. Готовый полигон можно бесплатно скачать в формате SVG.

Перейти

Как преобразовать растр в полигоны онлайн

Функциональный генератор для создания триангулярных изображений. Создает полигональную композицию из любого растрового изображения. Есть ряд настроек и кнопка рандомизации для получения случайных результатов. После  того как изображение будет готово Вы сможете скачать его в форматах PNG и SVG.

Перейти

Полигональные логотипы

На волне популярности полигональной графики стали создаваться логотипы в таком стиле

Создаем полигональный логотип в программе CorelDraw

Полигональный портрет

Эта техника позволяет создавать работы любой сложности.

В этих уроках показано, как создать полигональный портрет

Заставка — источник

Что такое полигональная графика? — Каждый пиксель важен

Хотите больше узнать о полигональной графике? Для чего она используется? Как сделать что-то в этой технике? Да? Тогда вы настоящий дизайнер, готовый развиваться, и расти как профессионал!

Конечно, полигональную графику вряд ли можно назвать чем-то новым, и уж тем более революционным. Тем не менее, она поможет разнообразить ваш дизайн и сделает его индивидуальным и узнаваемым. Да и очередной всплеск моды на полигоны, который бодро шагает по просторам Интернета, трудно игнорировать.

В этом посте вы узнаете о полигонах и полигональной графике и увидите потрясающие примеры ее использования. Также мы собрали для вас несколько уроков, которые помогут вам освоить эту технику. И, кто знает, может быть, вы будете рисовать полигонами даже круче, чем авторы собранных здесь работ!

Что такое полигональная графика?

Полигон (от греч. polýgonos – многоугольный), полигональная линия (математическая), ломаная линия, составленная из конечного числа прямолинейных отрезков (звеньев). Под полигоном также понимают замкнутую ломаную линию, т. е. многоугольник.

Ответ очевиден – в цифровой графике, конечно же! Это своего рода разновидность цифрового искусства. Изначально полигональная графика появилась в 3D моделировании для создания видеоигр. Благодаря низкому разрешению у таких объектов была высокая скорость рендеринга. Также отображение в виде каркаса позволяет экономить ресурсы компьютера и облегчает работу с моделью. Затем уже она стала популярна и в так называемой 2D графике.

Если вы работаете в 3D, то для вас будет вполне естественно делать это в 3D max, Maya, или Cinema 4D. Последнее ПО настолько дружелюбно, что в нем может рисовать даже ребенок. В целом, полигональная графика достаточно проста в создании, особенно если сравнивать с архитектурной визуализацией или фотореалистичным рендерингом. Она напоминает ранние дни компьютерного моделирования и анимации с налетом современных техник. А так как ретро стиль всегда в моде, практически все дизайнеры создают ее с помощью старых приемов.

Как вы уже знаете, 3D модели создают с помощью полигонов. Чем больше полигонов, тем более детализованной будет модель. Во время финальной обработки (рендеринга) объекта он приобретает «гладкий» вид. Чем меньше полигонов вы используете на стадии моделирования, тем более абстрактным будет результат. Для выраженного эффекта можно отключить функцию сглаживания в настройках рендеринга, и тогда вы получите четкие грани. Здесь все зависит от эффекта, которого вы хотите достичь. Использование низкополигональной техники совсем не означает, что сцена будет простой. Вы можете использовать сложные текстуры, реалистичные настройки отражений и преломлений в окружающей среде и т. д. Полигональные фигуры очень напоминают оригами и сейчас находятся на пике популярности в графическом дизайне.

Также можно создавать полигональные шедевры в таких программах как Adobe Illustrator, CorelDraw и даже Adobe Photoshop. Эти программы, в отличие от специфичных 3D пакетов, хорошо знакомы большинству дизайнеров.

А знаете ли вы, что полигональному дизайну предшествовало целое направление в искусстве? В начале XX века зародилось и стало невероятно популярным экспрессионистское течение. Появление фотографии только подстегивало художников, ведь теперь можно было запечатлеть образ детально, таким, какой он есть на самом деле. Экспрессионисты же напротив, стремились передать суть, настроение и характер объекта. Они намеренно уходили от деталей.  В наши дни экспрессионизм не менее популярен как в живописи, так и в среде цифрового искусства.

Вот несколько примеров современного цифрового искусства. Быть может, они впечатлят вас на создание новых шедевров:

Железный человек

The Kingdom – The King

Свобода

The little Power Giant

Wedding Invitations

Портрет Лила Уэйна

1. Создание векторных полигонов в Illustrator

В этом уроке вы создадите мозаику в Adobe Illustrator, состоящую из полигонов. В этом несложном деле поможет бесплатный плагин – Scriptographer  и ваше воображение.

1. Как создать векторную полигональную мозаику лайма

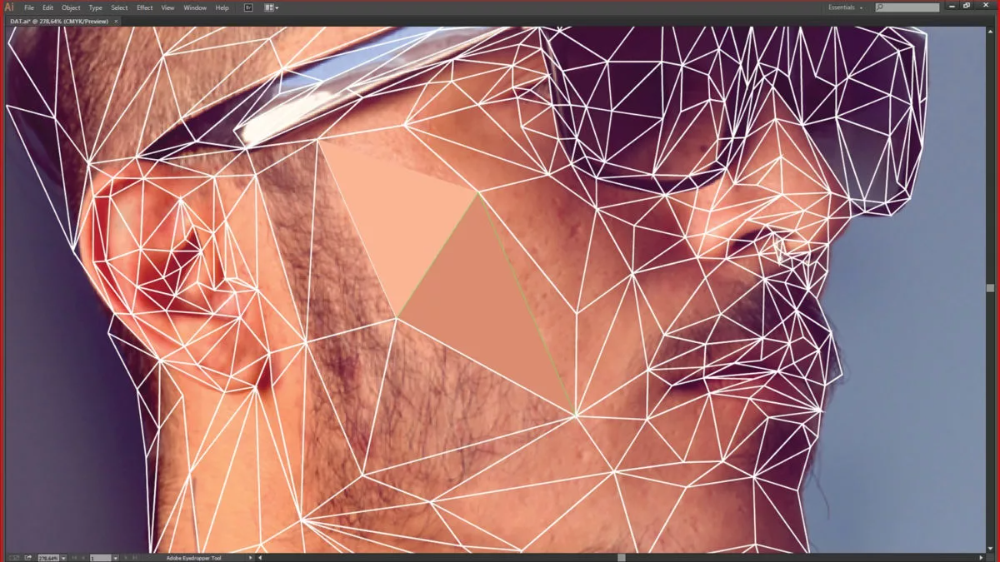
Здесь вы научитесь создавать векторную полигональную мозаику из растрового изображения при помощи бесплатного веб инструмента Triangulator и Adobe Illustrator.

1. Создание полигональной графики. Урок в 2-х частях

В этом уроке вы узнаете, как делать портреты с помощью полигонов. Автор показывает, как работать с фото используя и Photoshop и Illustrator, чтобы сделать красивый портрет в модном стиле полигональной графики.

1. Создание полигональной иллюстрации в Photoshop CS6

Этот урок так же подходит вам, если вы работаете в более ранних версиях Photoshop.

1. Создание низкополигональной модели в Cinema 4D

Подробный видео урок, который научит вас создавать трехмерные персонажи.

Полигональная графика – это смесь ретро и футуризма. Стиль не подвластный времени, который можно видоизменять, индивидуализировать, и экспериментировать с ним до бесконечности. Это всегда смотрится стильно, модно и самобытно. Попробуйте поработать с полигонами, и вы поймете, что уже больше не можете без них. Будем рады, если вы поделитесь своими идеями на этот счет в комментариях!

По материалам сайта: www. onextrapixel.com

russiachina-forum.com

Типы многоугольников — GeeksforGeeks

Многоугольник — это не что иное, как замкнутая фигура (соединенная встык), состоящая из более чем двух отрезков на двумерной плоскости. Слово Polygon состоит из двух слов: первое Poly означает «много», а gons означает «стороны». Многоугольник означает не что иное, как форму, имеющую много сторон. Или, другими словами, многоугольник создается с использованием прямолинейных отрезков, которые соединены друг с другом встык, и эти отрезки называются сторонами многоугольника, а точка называется вершиной многоугольника. Если фигура не содержит сторон и углов, то она не является многоугольной окружностью. Некоторые из полигонов: 

Свойства многоугольника:

• Мера каждого внешнего угла n-стороннего правильного многоугольника будет равна 360°/n.
• Мера каждого внутреннего угла n-стороннего правильного многоугольника будет [(n – 2) × 180°]/n.
• Количество треугольников, образованных соединением диагоналей из одного угла многоугольника, будет n – 2.
• Количество диагоналей в многоугольнике с n сторонами будет n(n – 3)/2.
• Сумма всех внутренних углов n-стороннего многоугольника будет (n – 2) × 180°.

Терминология:

1. Диагонали: Отрезок, соединяющий две непоследовательные вершины многоугольника, называется диагональю. Например, на данном рисунке AC и BD — две диагонали квадрата ABCD.

2. Смежные стороны: В многоугольнике, если две стороны имеют общую вершину, то такие стороны называются смежными сторонами. Например, на приведенном выше рисунке AD и DC являются смежными сторонами.

3. Смежная вершина: В многоугольнике, если две конечные точки или вершина одной стороны, то такой тип вершины известен как смежная вершина. Например, на приведенном выше рисунке вершины A и B являются соседними вершинами стороны AB.

Типы многоугольников:

Существует 4 типа многоугольников:

• Правильный многоугольник: Если все стороны и внутренние углы многоугольника равны или если многоугольник равноугольный и равносторонний, то многоугольник будет известен как правильный многоугольник. Пример квадрат, ромб, равносторонний треугольник и т. д.

• Неправильный многоугольник: Если все стороны и внутренние углы многоугольника имеют разную величину, то такой многоугольник называется неправильным многоугольником. Пример разностороннего треугольника, прямоугольника, воздушного змея и т. д.

• Выпуклый многоугольник: Если все внутренние углы многоугольника строго меньше 180° ^{или если отрезок прямой между двумя точками на границе не выйти за пределы многоугольника, то многоугольник будет известен как выпуклый многоугольник.}

• Вогнутый многоугольник: Если один или несколько внутренних углов многоугольника больше 180° градусов или многоугольник содержит хотя бы один отраженный внутренний угол, то такой многоугольник называется вогнутым многоугольником. Этот многоугольник может иметь по крайней мере четыре стороны.

Углы многоугольника:

В многоугольниках есть два типа углов:

• Внутренний угол: Это угол внутри фигуры, или мы можем сказать, что форма угла внутри многоугольника и сумма внутренних углов многоугольника

Сумма внутренних углов = (n – 2) x 180,

Здесь n – общее количество сторон многоугольника

или

Внутренний угол = 180° – Внешний угол,

или в радианах,

Сумма внутренних углов= = (n – 2)π радиан.

Например:

• Внешний угол: Это угол, образованный стороной и продолжением смежной стороны, а сумма внешних углов многоугольника равна 360 ^или . Сумма внешних углов многоугольника равна

Внешний угол = 180° – Внутренний угол

Если многоугольник имеет n сторон, то

Сумма всех внешних углов = n x 180° – сумма всех внутренних угол

Важные моменты:

• В каждом многоугольнике сумма внешних углов всегда будет 360°.
• Для правильного многоугольника размер каждого внешнего угла = 360° ÷ количество сторон.
• Для правильного многоугольника количество сторон = 360° ÷ размер внешнего угла.

Например:

Классификация многоугольников

Многоугольники классифицируются на основе количества сторон или вершин, которые они имеют. Итак, некоторые из многоугольников:

Полигон	№ сторон	Нет. 0159	3	0	3	60
Quadrilateral	4	2	4	90
Pentagon	5	5	5	108
Hexagon	6	9	6	120
Heptagon	7	14	7	128.571
Octagon	8	20	8	135
Nonagon	9	27	9	140
Decagon	10	35	10	144
Hendecagon	11	44	11	147,273
Dodecagon	12	54	12	54	12	54	12	54	12	54	0159	13	65	13	15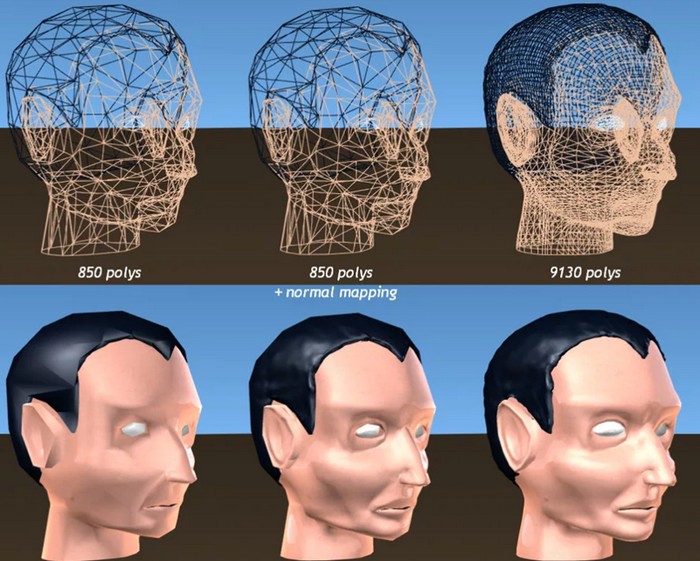8. 308
Tetrakaidecagon	14	77	14	154.286
Pentadecagon	15	90	15	156

Треугольники(3-угольник)

Треугольник — это многоугольник, он образован с помощью пересекающихся друг с другом отрезков из трех прямых, поэтому треугольник имеет 3 вершины, 3 ребра и 3 угла. Треугольники делятся на разные типы в зависимости от сторон и углов.

Некоторые свойства треугольника:

• Площадь треугольника: 1/2 × основание × высота
• В треугольнике сумма всех внутренних углов треугольника равна 180 ^o .
• Сторона, противоположная наибольшему углу, является наибольшей стороной треугольника.
• Периметр треугольника равен сумме длин всех трех сторон треугольника.

По сторонам:

• Равносторонний треугольник: Если треугольник имеет равные все стороны и равные углы, то такие типы треугольников известны как равносторонний треугольник.
• Равнобедренный треугольник: Если какой-либо треугольник имеет равные любые 2 стороны и углы, противоположные равным сторонам, равны, то такие типы треугольников известны как равнобедренные треугольники.
• Разносторонний треугольник: Если треугольник, у которого все 3 стороны не равны, то такие типы треугольников известны как разносторонний треугольник.

На основе угла:

• Остроугольный треугольник: Треугольник, каждый угол которого меньше 90°, то такой тип треугольника известен как остроугольный треугольник.
• Прямоугольный треугольник: Если любой из трех углов треугольника равен 90°, то такой тип треугольника называется прямоугольным.
• Тупоугольный треугольник: Если какой-либо из углов треугольника больше 90°, то такой тип треугольника известен как тупоугольный треугольник.

Четырехугольники (4-угольники) 

Четырехугольник — это не что иное, как многоугольник, имеющий по крайней мере 4 стороны. Многоугольник формируется путем включения четырех отрезков так, чтобы они пересекались друг с другом в вершинах, образуя 4 или более углов. Пример: Квадрат, Прямоугольник, Параллелограмм, Ромб, Трапеция.

Некоторые свойства четырехугольника:

• Четырехугольник.
• Имеет четыре вершины.
• В четырехугольнике сумма всех внутренних углов равна 360 ^o .

Примеры задач

Вопрос 1. Найдите внешний угол правильного шестиугольника?

Решение: 

Поскольку мы знаем, что шестиугольник имеет 6 сторон, следовательно,

Внешний угол = 360 ^o / n = 360 ^o / 6

Внешний угол = 60 ^o

Вопрос 2. Найдите внутренний угол правильного пятиугольника?

Решение:

Как мы знаем, что Пентагон имеет 5 сторон, поэтому

Внешний угол = 360 ^O /5 = 72 ^O

Угла внутреннего внутреннего угла = 1801107 O — 72

Угла внутреннего угла = 180 ^— —

. о = 108 ^о  

Вопрос 3. Найдите каждый внутренний угол правильного десятиугольника.

Решение : 

Как мы знаем, у десятиугольника десять сторон.

Используя формулу суммы углов, × 180°

= 8 × 180° = 1440°

Поскольку мы знаем, что все внутренние углы правильного десятиугольника равны,

Следовательно, мера каждого внутреннего угла правильного десятиугольника = сумма внутренних углов / количество сторон

Внутренний угол = 1440 / 10 = 144°

Следовательно, сумма внутренних углов десятиугольника равна 1440° и каждый внутренний угол составляет 144°.

Вопрос 4. Найдите значение x на данном рисунке:

Решение:

Так как мы знаем, что сумма углов четырехугольника 90 8 8 9 = 1070 90 3600003

so, 55 ^o + 124 ^o + 70 ^o + x = 360 ^o

249 ^o + x = 360 ^o

x = 111 ^o

Вопрос 5. Найдите значение x на данном рисунке:

Решение:

Так как мы знаем, что сумма внешних углов = 360 ^o

Значит, 120 10 8 901 +

2 х = 360 ^о

245 ^о + x = 360 ^O

x = 360 ^O — 245 ^O

x = 115 ^O

SVG Polygon

❮ предыдущий Далее ❯

Полигон SVG —

Элемент используется для создания графики, содержащей не менее три стороны.

Многоугольники состоят из прямых линий, а форма «замкнутая» (все линии подключиться).

Многоугольник происходит от греческого. «Поли» означает «много», а «гон» означает «угол».

---

Пример 1

В следующем примере создается многоугольник с тремя сторонами:

К сожалению, ваш браузер не поддерживает встроенный SVG.

Вот код SVG:

Пример

Попробуйте сами »

Объяснение кода:

• Атрибут points определяет координаты x и y для каждый угол многоугольника

---

Пример 2

В следующем примере создается многоугольник с четырьмя сторонами:

К сожалению, ваш браузер не поддерживает встроенный SVG.

Вот код SVG:

Пример

Попробуйте сами »

---

---

Пример 3

Используйте элемент для создания звезды:

К сожалению, ваш браузер не поддерживает встроенный SVG.

Вот код SVG:

Пример

  style=»fill:lime;stroke:purple;width-stroke:5;fill-rule:nonzero;» />

Попробуйте сами »

---

Пример 4

Измените свойство правила заполнения на «evenodd»:

К сожалению, ваш браузер не поддерживает встроенный SVG.

Вот код SVG:

Пример

  style=»fill:lime;stroke:purple;stroke-width:5;fill-rule:evenodd;» />

Попробуйте сами »

❮ Предыдущая Следующий ❯

ВЫБОР ЦВЕТА

---

---

---

Лучшие учебники

Учебное пособие по HTML
Учебное пособие по CSS
Учебное пособие по JavaScript
Учебное пособие
Учебное пособие по SQL
Учебное пособие по Python
Учебное пособие по W3. CSS
Учебник по Bootstrap
Учебник по PHP
Учебник по Java
Учебник по C++
Учебник по jQuery

Лучшие ссылки

HTML Reference
CSS Reference
JavaScript Reference
SQL Reference
Python Reference
W3.CSS Reference
Bootstrap Reference
PHP Reference
HTML Colors
Java Reference
Angular Reference
jQuery Reference

7 Top8 Examples Примеры HTML
Примеры CSS
Примеры JavaScript
How To Примеры
Примеры SQL
Примеры Python
Примеры W3.CSS
Примеры Bootstrap
Примеры PHP
Примеры Java
Примеры XML
Примеры jQuery

---

FORUM | О

W3Schools оптимизирован для обучения и обучения. Примеры могут быть упрощены для улучшения чтения и обучения. Учебники, ссылки и примеры постоянно пересматриваются, чтобы избежать ошибок, но мы не можем гарантировать полную правильность всего содержания.