Как узнать номер вк | Сервис поиска аудитории ВКонтакте vk.barkov.net
Ваши поисковые вопросы ВКонтакте отработают наши инструменты Сервиса VK.BARKOV.NET,если вам нужно выполнить поиск открытых данных ВК, сделав это автоматизировано, быстро и качественно.
По ссылке https://vk.barkov.net/mobilephones.aspx вы сможете спарсить номера мобильных телефонов пользователей ВКонтакте.
Указывая айди пользователей ВК или группы ВКонтакте, запускайте парсер (инструмент) в поиск и он соберет за вас из блока данных “Контакты” те номера мобильных, которые сами пользователи ВК там указали.
Привязки аккаунтов ВК к номерам телефонов мы не парсим так как эту инфу ВК не предоставляет никому.
Для того, чтобы узнать номер вк, который вы сами не можете увидеть на странице определенного человека ВКонтакте, этот инструмент не подойдет, так как скрытую информацию мы не собираем.
Запустить скрипт для решения вопроса
Полезный небольшой видеоурок по этой теме
О сервисе поиска аудитории ВКонтакте
vk.
barkov.net — это универсальный набор инструментов, который собирает самые разнообразные данные из ВКонтакте в удобном виде.
Каждый инструмент (скрипт) решает свою задачу:
Например, есть скрипт для получения списка всех подписчиков группы.
А вот тут лежит скрипт для сбора списка всех людей, поставивших лайк или сделавших репост к конкретному посту на стене или к любым постам на стене.
Ещё есть скрипт для получения списка аккаунтов в других соцсетях подписчиков группы ВКонтакте.
И таких скриптов уже более 200. Все они перечислены в меню слева. И мы регулярно добавляем новые скрипты по запросам пользователей.
Запустить скрипт для решения вопроса
Полезные ответы на вопросы по этому же функционалу для сбора данных из ВКонтакте
Телефоны из информации о людях ВК
Нужно спарсить номера телефонов ВКонтакте
Узнать номера пользователей ВК
Есть база аккаунтов ВК, нужны их номера
Собрать в ВК номера телефонов людей по определенным критериям для дальнейшего их обзвона менеджерами
Отпарсить телефоны пользователей ВКонтакте
Как делать парсинг телефонов пользователей ВКонтакте?
Как собирать телефоны подписчиков конкурентов ВК?
Собрать номера в группе ВК и сгруппировать их по странам
Нужен номер телефона ВКонтакте
Вывести список пользователей с именами и телефонами ВКонтакте
Как узнать номер страницы вк
Узнать ID ВКонтакте по базе телефонов
Как посмотреть номера подписчиков групп ВК?
Инструмент, который собирает номера телефонов ВКонтакте
Парсить телефонные номера пользователей ВКонтакте
Найти ВКонтакте телефоны
Как найти номер телефона человека по его ВК профилю?
Как сделать сбор телефонов ВКонтакте?
Парсить телефонные номера вконтакте по списку id
Виртуальные номера для ВКонтакте | Разное
04.
09.2021, 15:34,
РазноеПодписаться на Telegram-канал
Подписаться в Google News
Поддержать в Patreon
В современном мире уже трудно представить жизнь человека без социальных сетей. Они зачастую занимают большую часть нашего повседневного общения. Часто всего мы для общения используем свой смартфон, ноутбук и другие гаджеты.
Общение в социальных сетях (Facebook, Instagram, ВКонтакте, Одноклассники и др.) возможен и без сим-карты. Для общения в первое время нужно будет номер ВК регистрации.
Со временем все социальные сетей ожесточают свои правила, и многие профили удаляются или попадают в бан, что и ограничивает прием смс ВКонтакте. Для новой регистрации нужно открыть новый профиль и при этом опять пройти смс регистрацию. Понятно, что каждый раз покупать новую сим-карту и сменить номер, не удобно и не выгодно, поэтому многие решают эту проблему путем использования виртуальных номеров ВКонтакте. Это и является причиной большого спроса виртуальных номеров.
Применение виртуальных номеров
Сейчас более чем когда-то люди беспокоятся о конфиденциальности и о сохранении личных данных. Многие не хотят публиковать и вставить в известность свой мобильный номер. Это решается способом виртуальных номеров.
Услуга Hot Telecom
Услуга Hot Telecom дает возможность зарегистрироваться в ВКонтанте быстро и надёжно. Давайте перечислим ряд преимуществ услуги виртуального номера для ВКонтакте Hot Telecom:
Виртуальный номер избавляет от привязки к сим карте и от привязки к телефону,
Нет обязательности покупки сим-карты,
Есть возможность открыть несколько личных профилей,
Легкие, быстрые и доступные условия покупки виртуальных номеров,
Возможность зайти в аккаунт без привязки к мобильному устройству и другие.
Временные виртуальные номера для ВКонтакте без сим-карты позволяют получить сообщения от всех адресатов. На какое устройство или адрес получать сообщения выбирайте вы во время настроек в личном кабинете.
Виды виртуальных номеров Hot Telecom
Виртуальные номера для ВКонтакте бывают одноразовыми и постоянными. Оплата за услугу одноразового виртуального номера осуществляется едино разно, а постоянный – каждый месяц.
Создание личного профиля с применением одноразового виртуального номера удобная услуга Hot Telecom, который даёт ряд других преимуществ:
Безопасность личной информации – никто не сможет узнать ваше местоположение, прочитать переписку, взломать базу паролей и т.д.,
Услуга дает возможность обходить местные регионные блокировки входа в социальные сети, например, в Украине есть ограничения использования ВКонтакте,
Возможность создать несколько акаунтов, что повышает вероятность побед в различных активностях,
Защита от хакеров и другие.
Смотреть комментарии
номер привязки в nLab
Пропустить навигационные ссылки | Домашняя страница | Все страницы | Последние версии | Обсудить эту страницу |
Номера связейКонтекст
Теория узлов
Теория узлов
узел , ссылка
изотопия
узел дополняет
диаграммы узлов, хордовая диаграмма
Движение Райдемайстера
Примеры/классы:
узел-трилистник
торический узел
одиночный узел
гиперболический узел
ссылка Борромео
Ссылка Уайтхеда
Звено Хопфа
Типы
простой узел
мутантный узел
инварианты узлов
пересечение номер
номер моста
номер развязывания
окрашиваемость
группа узлов
узел род?
инварианты полиномиальных узлов
(наблюдаемые непертурбативной теории Черна-Саймонса)
Многочлен Джонса
Полином ХОМФЛИ
Полином Александра
Инварианты Решетихина-Тураева
Инварианты узла Васильева
(наблюдаемые пертрубативной теории Черна-Саймонса)
Гомология Хованова
Кронштейн Кауфмана?
инварианты ссылок
Милнор мю-бар инварианты
номер привязки
Связанные понятия:
Васильев мотокотношение
Поверхность Зейферта
теория виртуальных узлов
Хирургия Дена, исчисление Кирби
объемная догадка
арифметическая топология
категория: теория узлов
Топология
топология (точечно-множественная топология, бесточечная топология)
см.
также дифференциальная топология , алгебраическая топология , функциональный анализ и топологическая гомотопическая теория
Введение
Основные понятия 83
открытое подмножество, закрытое подмножество, окрестности
топологическое пространство, локаль
для топологии, база окрестности
более тонкая/грубая топология
закрытие, внутреннее, граничное
разлука, трезвость
непрерывная функция, гомеоморфизм
равномерно непрерывная функция
встраивание
открытая карта, закрытая карта
последовательность, сеть, подсеть, фильтр
сходимость
категорияTop
- удобная категория топологических пространств
Универсальные конструкции
начальная топология, окончательная топология
подпространство, частное пространство,
оптоволоконное пространство, место для крепления
пространство продукта, пространство несвязного объединения
картографический цилиндр, картографический социлиндр
картографический конус, картографический кокон
картографический телескоп
копределы нормальных пространств
Дополнительный материал, структура, свойства
красивое топологическое пространство
метрическое пространство, метрическая топология, метризуемое пространство
Пространство Колмогорова, Хаусдорфово пространство, регулярное пространство, нормальное пространство
трезвое пространство
компактное пространство, правильная карта
секвенциально компактно, счетно компактно, локально компактно, сигма-компактно, паракомпактно, счетно паракомпактно, сильно компактно
компактно сгенерированное пространство
второй счетный пробел, первый счетный пробел
сжимаемое пространство, локально сжимаемое пространство
подключенное пространство, локально подключенное пространство
односвязное пространство, локально односвязное пространство
клеточный комплекс, CW-комплекс
заостренный пробел
топологическое векторное пространство, банахово пространство, гильбертово пространство
топологическая группа
топологическое векторное расслоение, топологическая K-теория
топологический коллектор
Примеры
пустое пространство, точечное пространство
дискретное пространство, содискретное пространство
Площадь Серпинского
топология порядка, топология специализации, топология Скотта
Евклидово пространство
- реальная линия, плоскость
- цилиндр
, конус
сфера, шар
круг, тор, кольцо, лента Мебиуса
многогранник, многогранник
проективное пространство (действительное, комплексное)
место для классификации
пространство конфигурации
путь, цикл
пространства отображений: компактно-открытая топология, топология равномерной сходимости
- пространство цикла, пространство пути
Топология Зарисского
пространство Кантора, пространство Мандельброта
Кривая Пеано
линия с двумя исходными пунктами, длинная линия, линия Sorgenfrey
K-топология, пространство Даукера
Варшавский круг, пространство для гавайских сережек
Основные положения
пространства Хаусдорфа трезвые
схемы трезвые
непрерывных образа компактных пространств компактны
замкнутых подпространства компактных хаусдорфовых пространств являются эквивалентно компактными подпространствами
открытых подпространства компактных хаусдорфовых пространств локально компактны
факторпроекции из компактных хаусдорфовых пространств замкнуты в точности, если кодовая область хаусдорфова
компактных пространства эквивалентно имеют сходящуюся подсеть каждой сети
лемма числа Лебега
секвенциально компактные метрические пространства являются эквивалентно компактными метрическими пространствами
компактных пространства эквивалентно имеют конвергентную подсеть каждой сети
секвенциально компактных метрических пространства вполне ограничены
Функция со значениями в непрерывном метрическом пространстве на компактном метрическом пространстве равномерно непрерывна
паракомпактных хаусдорфовых пространств нормальны
паракомпактных хаусдорфовых пространств эквивалентно допускают подчиненные разбиения единицы
закрытые инъекции являются вложениями
собственные отображения в локально компактные пространства закрыты
инъективных собственных отображения в локально компактные пространства эквивалентны замкнутым вложениям
локально компактные и сигма-компактные пространства паракомпактны
локально компактных и счетных до секунды пространств сигма-компактны
регулярных пространства со счетом секунд паракомпактны
CW-комплексы являются паракомпактными хаусдорфовыми пространствами
Теоремы
Лемма Урысона
Теорема расширения Титце
Теорема Тихонова
трубная лемма
Теорема Майкла
Теорема Брауэра о неподвижной точке
топологическая инвариантность размерности
Теорема о кривой Жордана
Теоремы анализа
Теорема Гейне-Бореля
теорема о промежуточном значении
теорема об экстремальных значениях
топологическая теория гомотопий
левая гомотопия, правая гомотопия
гомотопическая эквивалентность, деформационный ретракт
основная группа, покрывающая пространство
фундаментальная теорема о покрытии пространств
гомотопическая группа
слабая гомотопическая эквивалентность
Теорема Уайтхеда
Теорема Фрейденталя о подвеске
теорема о нервах
свойство гомотопического расширения, корасслоение Гуревича
последовательность cofiber
Стрём модель категории
классическая модельная структура на топологических пространствах
- Знаки пересечения
- Корчиться
- Номер привязки
- Примеры
- Инвариантность?
- Номер привязки является целым числом
На диаграмме ориентированных связей мы видим два типа возможных пересечений.
Они выделяются знаком + или -.
Один из способов запомнить правила знаков — представить подход к перекрестку вдоль 9-й0203 подземный переход в направлении ориентации:
- если подземный переход проходит слева направо, переход считается положительным ;
- , если он проходит справа налево, он считается отрицательным .
Изгиб
Изгиб ориентированного узла или звена диаграммы представляет собой сумму знаков всех ее пересечений. Если DD — диаграмма, мы обозначаем ее изгиб через w(D)w(D).
Изгиб используется в определении некоторых инвариантов узла.
Это вариант корчи, более адаптированный для использования со ссылками.
Предположим, что у нас есть ориентированная диаграмма связей DD с компонентами C1,…,CmC_1, \ldots, C_m, число связи CiC_i с CjC_j, где CiC_i и CjC_j являются различными компонентами DD, должно составлять половину суммы признаков пересечений CiC_i с CjC_j; он будет обозначаться lk(Ci,Cj)lk(C_i,C_j).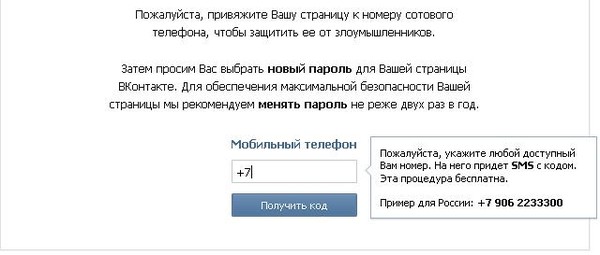
Число связей диаграммы DD тогда сумма чисел связей всех пар компонентов:
Lk(D)=∑1≤i Изгиб стандартного трилистника равен 3, звена Хопфа (оба компонента ориентированы по часовой стрелке) равно +2, а кольца Борромео равно 0, хотя это нетривиальное звено. Корч не является изотопическим инвариантом, так как его можно изменить, а скрутить стойку узла (или звена). Корч является инвариантом регулярной изотопии. Номер ссылки является инвариантом связи. Мы используем движения Рейдемейстера, поэтому необходимо проверить, не изменяют ли они номер связи диаграммы. Любое движение Рейдемейстера, которое включает по крайней мере два компонента связи (т. е. которое должно быть R2 или R3), оставляет все номера связей между компонентами неизменными. Ход R2 удаляет или вводит два перекрестка противоположного знака, в то время как ход R3 оставляет число пересечений и их знаки неизменными. Мы можем заключить, что зацепление Хопфа не изотопно двухкомпонентному разъединению (что обнадеживает), поскольку любое присвоение ориентации зацеплению Хопфа приводит к ненулевому числу зацеплений. Пусть n1n_{1} (соответственно n2n_{2}) будет суммой знаков пересечений между парой компонент L1L_{1} и L2L_{2} звена, в котором наддуга принадлежит L1L_{1 } (соответственно L2L_{2}). Таким образом, связующее число явно равно 12(n1+n2)\frac{1}{2}(n_{1} + n_{2}). Теперь возьмем пересечение между L1L_{1} и L2L_{2} так, чтобы дуга над дугой принадлежала L1L_{1}. Предположим, что мы переключили тип пересечения, так что теперь нижняя дуга принадлежит L1L_{1}. Тогда, независимо от знака пересечения, можно проверить, что сумма n1−n2n_{1} — n_{2} не меняется при этом переключении. Очевидно, что мы также можем переключать пересечения на самопересечения компонента или на пересечения двух рассматриваемых компонентов с другими компонентами, не затрагивая сумму n1−n2n_{1} — n_{2}. Кроме того, несложно проверить, что движения Рейдемейстера не изменяют сумму n1−n2n_{1} — n_{2}. Теперь очевидно, что любая пара компонентов ссылки может быть отсоединена от ссылки после выполнения соответствующих перекрестных переключений. В случае, когда L1L_{1} и L2L_{2} представляют собой окружности, не пересекающиеся друг с другом и с остальной частью звена, мы имеем, что n1−n2=0n_{1} — n_{2} = 0, Мы заключаем, что n1−n2=0n_{1} — n_{2} = 0 во всех случаях. Следовательно, n1=n2n_{1} = n_{2}, а число связей равно 12(2n1)=n1=n2\frac{1}{2}(2n_{1}) = n_{1} = n_{ 2}. В частности, номер ссылки является целым числом. Непосредственным следствием того факта, что сумма знаков пересечений между L1L_{1} и L2L_{2} четна, является то, что на самом деле должно быть четное число таких пересечений. Последняя редакция: 7 июня 2017 г., 19:09:44.
См. историю этой страницы для получения списка всех вкладов в нее. Связующее число является топологическим свойством ДНК. Связующее число — это сумма завихрений и корчей. Количество раз, когда одна нить ДНК оборачивается вокруг другой, называется поворотом, а взаимное закручивание двойной спирали называется корчей. Короче говоря, извитость — это количество раз, когда двойная спираль ДНК пересекается, накручивается друг на друга или количество раз, когда одна нить оборачивается вокруг другой. Согласно модели Уотсона и Крикса, эукариотическая ДНК является правозакрученной и имеет отрицательную суперспирализацию. Очень сложно понять топологию ДНК в двумерном пространстве, потому что топология — это наука, которую нельзя понять без свойства трехмерности. Чтобы понять номер привязки, мы можем предположить намотку модели телефонного провода. Тот же образец ДНК следует во время упаковки или суперспирализации. Подробнее об упаковке ДНК читайте в статье Упаковка ДНК у эукариот. Корчание ДНК более важно, так как это поможет в расположении ДНК. Здесь корчи могут быть перекручены или перекручены. Переплетенные корчи являются плектонемическими, что означает, что они наматываются друг на друга или вокруг оси. При перекрутке корчится по спирали. Классическим примером спиральной намотки является сборка гистонов и ДНК, дцДНК закручивается вокруг гистонов по спирали во время образования нуклеосом. Ключевые темы: Сумма общего количества изгибов и корчей называется числом связывания. Если оба конца ДНК соединены, число связей остается неизменным (число связей равно нулю в случае кольцевой молекулы ДНК). Итак, если мы хотим изменить номер связи, мы должны разорвать цепь ДНК, и эту функцию выполняет ДНК-топоизомераза. Числа близнецового пламени Пожалуйста, включите JavaScript Важно отметить, что скручивание и скручивание могут быть взаимопреобразовываемыми, в cccDNA при некоторых условиях искажения некоторые скручивания могут быть преобразованы в скручивания, а некоторые из скручиваний могут быть преобразованы в скручивания. Однако сумма обоих остается неизменной (поскольку Lk = Tw + Wr). Эукариотическая ДНК имеет форму В, правостороннюю и недозакрученную, что означает, что она имеет отрицательную сверхспирализацию. Левосторонняя ДНК положительно сверхспиральна и перекручена (не распространена в природе). Позже в этой части мы обсудим, почему важна отрицательная суперспирализация. При сверхспирализации ДНК извитость также зависит от крутки. Как мы знаем, скручивание зависит от осевого напряжения ДНК, когда число скручиваний увеличивается, это увеличивает торсионное напряжение на оси ДНК, и в конечном итоге скручивание будет увеличиваться. В кзкДНК корчи остаются нулевыми, так как между двухцепочечными ДНК не наблюдается взаимная спираль. здесь, если, Lk= Tw + Wr Для кзкДНК (writhe равно нулю) Итак, Lk= Tw. Изображение предоставлено: http://www.siumed.edu, изображение представляет собой количество связывающих молекул ДНК. на изображении a, Lk=1 и на b, Lk=6 Теперь представьте, что кзкДНК полностью релаксирована, что означает, что она не имеет суперспирализации, в этом состоянии число связывания становится равным нулю, поэтому сверхспирализация в кзкДНК обозначается как Lk 0 . Согласно модели Уотсона и Крика, двухцепочечная ДНК имеет 10,5 п.н. на спираль и является релаксированной. Расслабленная кзкДНК имеет в общей сложности 1050 п.н., поэтому общее число связей равно 9.0003 Число связей (Lk) = общее количество оснований/пар оснований на виток спирали следовательно, Lk= 1050 п. Lk= +100 (поскольку ДНК не является формой B и левосторонняя) Подробно указано, что если наша ДНК является левосторонней и имеет 10,5 п.н. на виток при длине 1050 п.н., то одна цепь перекрещивается или накручивается (положительная суперспирализация) на другую цепь 100 раз. Однако это всего лишь предполагаемый пример, поскольку полностью релаксированной ДНК (или положительно сверхскрученной ДНК) в природе не существует. Когда мы многократно уменьшаем изгибы и корчи, разрезая ферментом, число связей постепенно уменьшается и становится равным нулю. Следовательно, разность между номером связи (Lk) и нулевой связью (Lk 0 ) называется разностью связи ΔLk, Итак, ΔLk = Lk – Lk 0 Если значение ΔLk отлична от нуля ( >0 или <0 ), то ДНК называется сверхскрученной. Кроме того, Lk меньше, чем Lk 0 (число связей меньше нуля), ΔLk также <0, а полученное значение отрицательно, поэтому ДНК называется отрицательно суперскрученной. Аналогично, если Lk > Lk 0 , то ΔLk > 0, и полученное значение положительно, поэтому ДНК называется положительно сверхскрученной. Здесь значение ΔLk зависит от длины ДНК. Если длина увеличивается, сверхспирализация будет увеличиваться, и наоборот. Специфические различия в связывании являются еще одним важным свойством сверхспирализации. Ее также называют суперспиральной плотностью, которая представляет собой разницу между разностью связей (ΔLk) и количеством связей кзкДНК (Lk 0 ). Итак, Сверхспиральная плотность = ΔLk /Lk 0 Электрофорез в агарозном геле — это метод, с помощью которого мы можем идентифицировать различные формы молекул ДНК. Если у нас есть четыре молекулы ДНК одинаковой длины с разной топологией, каждая молекула по-разному мигрирует в агарозном геле. Предположим, что первая ДНК имеет тесную кольцевую форму без суперспирализации, а вторая молекула ДНК имеет обе цепи, скрученные вокруг друг друга, что означает линейную двухцепочечную ДНК. В каждом случае молекулы ДНК мигрируют по-разному. Более компактно суперскрученная ДНК быстрее мигрирует в геле. Следовательно, четвертая (сверхскрученная и компактная) мигрирует быстрее по сравнению с другой ДНК (дорожка C и D: полоса в основании). Изображение предоставлено: «Молекулярная биология гена», 7-е издание Watson. Изображение представляет миграцию различных молекул ДНК под гелем. Первая, кольцевая ДНК, не имеет суперспирализации, поэтому мигрирует медленнее, чем любая другая ДНК, и остается последней (дорожки A и D). Чем компактнее ДНК, тем легче она проходит через поры агарозы. Таким образом, кольцевая ДНК остается последней, линейная ДНК покрывает большее расстояние, чем кольцевая ДНК, а спиральная ДНК покрывает большее расстояние, чем линейная ДНК. Наконец сверхспиральная ДНК преодолевает большее расстояние, чем любая другая ДНК, и работает быстрее. Примеры
Инвариантность?
Предложение
Предложение
Доказательство
Топология ДНК.
Что такое число связей ДНК?
siumed.edu
Изображение представляет собой сверхспирализацию телефонного провода.
siumed.edu, изображение представляет связующее число в отрицательной сверхспирализации и положительной сверхспирализации.
Это изменение делает ДНК сверхскрученной и еще более плотной упакованной на хромосоме.
н. / 10,5 (п.н./виток)
Идентификация различных форм ДНК 
Положительная сверхспирализация хранит больше энергии, поэтому даже при более высоких температурах ДНК не денатурирует. Даже фермент не может распознать положительно суперскрученную ДНК и не может ее разрезать.
Третья молекула ДНК накручена вокруг друг друга с некоторыми изгибами, а четвертая сверхскручена.