Перевод чисел в различные системы счисления с решением | Онлайн калькулятор
Калькулятор позволяет переводить целые и дробные числа из одной системы счисления в другую. Основание системы счисления не может быть меньше 2 и больше 36 (10 цифр и 26 латинских букв всё-таки). Длина чисел не должна превышать 30 символов. Для ввода дробных чисел используйте символ . или ,. Чтобы перевести число из одной системы в другую, введите исходное число в первое поле, основание исходной системы счисления во второе и основание системы счисления, в которую нужно перевести число, в третье поле, после чего нажмите кнопку «Получить запись».
Исходное число записано в 23456789101112131415161718192021222324252627282930313233343536-ой системе счисления.
Хочу получить запись числа в 23456789101112131415161718192021222324252627282930313233343536-ой системе счисления.
Получить запись
=
Выполнено переводов:
Также может быть интересно:
Системы счисления
Пример 1. Возьмём число 5921 в десятичной системе счисления. Пронумеруем число справа налево начиная с нуля:
| Число: | 5 | 9 | 2 | 1 |
| Позиция: | 3 | 2 | 1 | 0 |
Число 5921 можно записать в следующем виде: 5921 = 5000+900+20+1 =
Пример 2. Рассмотрим вещественное десятичное число 1234.567. Пронумеруем его начиная с нулевой позиции числа от десятичной точки влево и вправо:
| Число: | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Позиция: | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Число 1234.567 можно записать в следующем виде: 1234.567 = 1000+200+30+4+0.5+0.06+0.007 = 1·10.
Перевод чисел из одной системы счисления в другую
Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2. Найдём сумму произведений цифр числа на основание системы счисления в степени позиции этой цифры:
1. Перевести число 1001101.1101 в десятичную систему счисления.
Решение: 10011.11012 = 1·24+0·23+0·22+1·21+1·20+1·2-1+1·2-2+0·2-3+1·2-4 = 16+2+1+0.5+0.25+0.0625 = 19.812510
Ответ: 10011.11012 = 19.812510
2. Перевести число E8F.2D16 в десятичную систему счисления.
Решение: E8F.2D16 = 14·162+8·161+15·160+2·16-1+13·16-2 = 3584+128+15+0.125+0.05078125
3727.1757812510Ответ:
E8F.2D16 = 3727.1757812510Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.
Перевод целой части числа из десятичной системы счисления в другую систему счисления
Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.
3. Перевести число 27310 в восьмиричную систему счисления.
Проверка:
4·82+2·81+1·80 = 256+16+1 = 273 = 273, результат совпал. Значит перевод выполнен правильно.Ответ:
27310 = 4218Рассмотрим перевод правильных десятичных дробей в различные системы счисления.
Перевод дробной части числа из десятичной системы счисления в другую систему счисления
Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.
4. Перевести число 0.12510 в двоичную систему счисления.
Решение: 0.125·2 = 0.25 (0 — целая часть, которая станет первой цифрой результата), 0.25·2 = 0.5 (0 — вторая цифра результата), 0.5·2 = 1.0 (1 — третья цифра результата, а так как дробная часть равна нулю, то перевод завершён).
Ответ: 0.12510 = 0.0012
programforyou.ru
Системы счисления. Перевод из одной системы в другую.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 1100 | 110 | 22 | |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
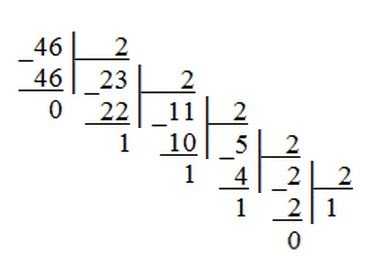
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
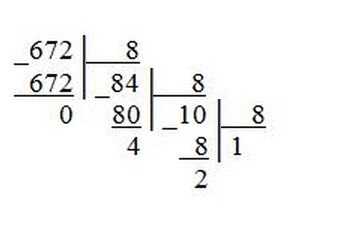
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т.е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Пи (число) — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Пи.| Иррациональные числа ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — eπ{\displaystyle e^{\pi }} и π | |
| Система счисления | Оценка числа π{\displaystyle \pi } |
| Десятичная | 3,1415926535897932384626433832795… |
| Двоичная | 11,00100100001111110110… |
| Шестнадцатеричная | 3,243F6A8885A308D31319… |
| Шестидесятеричная | 3; 08 29 44 00 47 25 53 07 … |
| Рациональные приближения | 22⁄7, 179⁄57, 223⁄71, 333⁄106, 355⁄113, 103 993⁄33 102 (перечислено в порядке увеличения точности) |
| Непрерывная дробь | [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, … ] (Эта непрерывная дробь не периодическая. Записана в линейной нотации) |
| Тригонометрия | π{\displaystyle \pi } радиан = 180° |
3,1415926535 8979323846 2643383279 5028841971 6939937510
5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128
4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091
4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436
7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548
0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798
6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872
1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960
5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881
7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778
1857780532 1712268066 1300192787 6611195909 2164201989
…
Число π{\displaystyle \pi } с первой тысячей высших разрядов десятичной дроби[1] Если диаметр окружности равен единице, то длина окружности — это число «пи»
π{\displaystyle {\boldsymbol {\pi }}} (произносится «пи») — математическая постоянная, равная отношению длины окружности к её диаметру[K 1]. Обозначается буквой греческого алфавита «π».
Трансцендентность и иррациональность[править | править код]
Число π{\displaystyle \pi } иррационально, то есть его значение не может быть точно выражено в виде дроби mn{\displaystyle {\frac {m}{n}}}, где m{\displaystyle m} и n{\displaystyle n} — целые числа. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. Иррациональность числа π{\displaystyle \pi } была впервые доказана Иоганном Ламбертом в 1761 году[2] путём разложения тангенса в непрерывную дробь. В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел π{\displaystyle \pi } и π2{\displaystyle \pi ^{2}}.
π{\displaystyle \pi } — трансцендентное число, то есть оно не может быть корнем какого-либо многочлена с целыми коэффициентами. Трансцендентность числа π{\displaystyle \pi } была доказана в 1882 году профессором Кёнигсбергского, а позже Мюнхенского университета Линдеманом. Доказательство упростил Феликс Клейн в 1894 году[3]. Поскольку в евклидовой геометрии площадь круга и длина окружности являются функциями числа π{\displaystyle \pi }, то доказательство трансцендентности π{\displaystyle \pi } положило конец попыткам построить квадратуру круга, длившимся более 2,5 тысяч лет.
В 1934 году Гельфонд доказал[4] трансцендентность числа eπ{\displaystyle e^{\pi }}. В 1996 году Юрий Нестеренко доказал, что для любого натурального n{\displaystyle n} числа π{\displaystyle \pi } и eπn{\displaystyle e^{\pi {\sqrt {n}}}} алгебраически независимы, откуда, в частности, следует[5][6] трансцендентность чисел π+eπ,πeπ{\displaystyle \pi +e^{\pi },\pi e^{\pi }} и eπn{\displaystyle e^{\pi {\sqrt {n}}}}.
π{\displaystyle \pi } является элементом кольца периодов (а значит, вычислимым и арифметическим числом). Но неизвестно, принадлежит ли 1/π{\displaystyle 1/\pi } к кольцу периодов.
Соотношения[править | править код]
Известно много формул для вычисления числа π{\displaystyle \pi }:
- 2π=22⋅2+22⋅2+2+22⋅…{\displaystyle {\frac {2}{\pi }}={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdot \ldots }
- Это первое известное явное представление π{\displaystyle \pi } с бесконечным числом операций. Доказать его можно следующим образом. Применив тождество sin2φ=2sinφcosφ{\displaystyle \sin 2\varphi =2\sin \varphi \cos \varphi } рекурсивно и перейдя к пределу, получим
- φcosφ2cosφ4⋯=sinφ.{\displaystyle \varphi \cos {\dfrac {\varphi }{2}}\cos {\frac {\varphi }{4}}\cdots =\sin \varphi .}
- Остаётся подставить φ=π2{\displaystyle \varphi ={\frac {\pi }{2}}} и воспользоваться формулой косинуса двойного угла: cos2φ=cos2φ−sin2φ.{\displaystyle \cos 2\varphi =\cos ^{2}\varphi -\sin ^{2}\varphi .}
- 21⋅23⋅43⋅45⋅65⋅67⋅87⋅89⋯=π2{\displaystyle {\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots ={\frac {\pi }{2}}}
- 11−13+15−17+19−⋯=π4{\displaystyle {\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-\cdots ={\frac {\pi }{4}}}
- 112+122+132+142+152+⋯=π26{\displaystyle {\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+{\frac {1}{5^{2}}}+\dots ={\frac {\pi ^{2}}{6}}} (ряд обратных квадратов)
- π=12∑k=0∞116k(88k+2+48k+3+48k+4−18k+7)==14∑k=0∞116k(88k+1+88k+2+48k+3−28k+5−28k+6−18k+7)==∑k=0∞(−1)k4k(24k+1+24k+2+14k+3){\displaystyle {\begin{aligned}\pi &={\frac {1}{2}}\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {8}{8k+2}}+{\frac {4}{8k+3}}+{\frac {4}{8k+4}}-{\frac {1}{8k+7}}\right)=\\&={\frac {1}{4}}\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {8}{8k+1}}+{\frac {8}{8k+2}}+{\frac {4}{8k+3}}-{\frac {2}{8k+5}}-{\frac {2}{8k+6}}-{\frac {1}{8k+7}}\right)=\\&=\;\;\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{4^{k}}}\left({\frac {2}{4k+1}}+{\frac {2}{4k+2}}+{\frac {1}{4k+3}}\right)\end{aligned}}}
- π=23∑k=0∞(−1)k3k(2k+1){\displaystyle \pi =2{\sqrt {3}}\sum \limits _{k=0}^{\infty }{\frac {(-1)^{k}}{\,3^{k}\,(2k+1)}}}
- π=8∑k=1∞∑m=1∞1(4m−2)2k=4∑k=1∞∑m=1∞m2−k2(m2+k2)2=360∑k=1∞∑m=1k1m(k+1)34{\displaystyle \pi =8\sum \limits _{k=1}^{\infty }\sum \limits _{m=1}^{\infty }{\frac {1}{(4m-2)^{2k}}}=4\sum \limits _{k=1}^{\infty }\sum \limits _{m=1}^{\infty }{\frac {m^{2}-k^{2}}{(m^{2}+k^{2})^{2}}}={\sqrt[{4\,\,}]{360\sum \limits _{k=1}^{\infty }\sum \limits _{m=1}^{k}{\frac {1}{m(k+1)^{3}}}}}}
- π=limm→∞(m!)424m[(2m)!]2m{\displaystyle \pi =\lim \limits _{m\rightarrow \infty }{\frac {(m!)^{4}\,{2}^{4m}}{\left[(2m)!\right]^{2}\,m}}}
- π=6limn→∞∏k=1pk∈Pn(1−1pk2)→{\displaystyle \pi ={\sqrt {\frac {6}{\lim \limits _{n\to \infty }\prod \limits _{k=1 \atop p_{k}\in \mathbf {P} }^{n}\,\left(1-{\frac {1}{p_{k}^{2}}}\right)}}}\quad \to } здесь pk{\displaystyle p_{k}} — простые числа
- π=limn→∞2n2−2+2+2+⋯+2,{\displaystyle \pi =\lim _{n\to \infty }2^{n}{\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+\dots +{\sqrt {2}}}}}}}}}},} где n{\displaystyle n}
ru.wikipedia.org
Онлайн прописи для письма. Буквы и цифры
Сейчас ни для кого не является секретом тот факт, что время на обучение ребенка правильному каллиграфическому письму в первом классе сведено к минимуму.
Успеть бы показать, как буква пишется и читается.
И от этой спешки неокрепшие пальчики ребенка начинают через некоторое время выводить такие каракули, что о написанном можно только догадываться.
Закрепить навык письма, выработать автоматическое правильное и что самое главное понятное написание письменных букв помогают дополнительные занятия с прописями.
На этой страничке вашему вниманию представлен онлайн-сервис по генерированию прописей, которые вы можете составить самостоятельно с учетом всех проблем и потребностей вашего ребенка.
Генератор прописей преобразует введенный вами текст в рукописные прописи, применяя специально созданный каллиграфический шрифт с пунктирной и сплошной линией.
Генератор прописей
Чтобы составить прописи, выберите на панели нужные вам функции.
Вид страницы: в косую линию, в узкую линию, в широкую линию.
Выбор страницы зависит от степени подготовленности вашего ребенка.
Для написания цифр используйте страницу в клетку.
Вид шрифта: пунктирный, сплошной серый, сплошной черный.
Для обводки букв выберете пунктирный шрифт или сплошной серый.
Для самостоятельного письма по примеру — сплошной черный.
Положение страницы: книжное, альбомное.
В отдельной строке напишите задание.
Например: обведи буквы, пропиши по образцу, пропиши самостоятельно по образцу и т.п.
Далее заполните форму текстом на свое усмотрение.
Это могут быть отдельные буквы, слоги, слова. Пропишите те буквы и слоги, при написании которых у вашего ребенка возникают трудности.
Вы можете вписать предложения или текст (стихотворение, загадку).

Для перехода на новую строку и корректного отображения текста используйте кнопку ENTER.
В книжном формате ширина строки порядка 40-42 знака, учитывая пробелы. В альбомном формате ширина строки порядка 55-58 знаков.
С помощью онлайн генератора прописей вы можете составить, скачать и распечатать задания для детей любой сложности.
Вы можете создать прописи не только на кириллице. Используя латинскую раскладку клавиатуры, вы можете сгенерировать прописи по английскому и немецкому языку.
Для дошкольного возраста используйте пунктирный шрифт и страницу с косой линией.
Пропишите отдельные строчные и заглавные буквы, слоги и слова для обводки.
Для первоклассников можно создать прописи уже со сплошной линией.
Вы можете написать по одному примеру, оставив строку пустой для самостоятельного письма.

Вы так же можете с помощью генератора прописей составить грамматическое упражнение для ребенка.
Напишите слова или текст с пропущенными буквами. Это могут быть словарные слова, слова с проверочными гласными, слова с приставками и т.п.
Не забудьте про цифры 🙂
Используйте страницу в клетку и пунктирный шрифт. Можно распечатать не только прописи с цифрами, но и прописи с математическими примерами, составив их самостоятельно.
Напомню, что если вам необходимы задания с математическими примерами по математике воспользуйтесь Генератором примеров, который поможет вам создать и распечатать математические примеры для детей разного уровня подготовки.
Надеюсь, что сервис по созданию прописей поможет вам в обучении ваших детей.
Данный генератор будет полезен для составления прописей, как для дошкольников, так и для школьников младших классов.
Для самых маленьких подойдут уже готовые развивающие прописи.
Если вдруг у вас возникнут трудности или вопросы — обязательно пишите в комментариях.
Буду рада обратной связи, отзывам и предложениям.
Так же буду признательна за поддержку в развитии генератора :))
Читайте похожие записи:
tobemum.ru
Как сделать патрон-переходник с Е27 на Е14
Раздел: ЖизньНаписано: 15.05.2009
Автор: Antonio
Предыстория.
Купили с женой в супермаркете энергосберегающие лампочки, меня подкупила мощность и цена.
15W (аналог обычной 75 Вт) — 9 грн с копейками (~1,1$)
20W (аналог по идее 100Вт) — 7 грн с копейками (~0,88$)
Красивенькие рисунки на коробках, дешевая цена, и должны светить — и это все для подъезда, чтобы там было светло и уютно :-).
Проверять их там не стали и даже не открывали, взяли и пошли.
Полежали они у меня недельку дома и решил я одну лампочку вкрутить и тут на тебе!
Маленький цоколь Е14!
Я не ожидал такого подвоха, ладно думаю, поищем переходник.
Спросил у знакомого электрика, он не видел таких переходников, прошелся по рынку и магазинам, тоже нету.
Нашел в инете картинку переходника FB24-14.
Дальше для тех, кто готов потратить 10 минут на изготовление патрона-переходника
В строительном магазине я нашел патрон под такой маленький цоколь, стоил он 2,5 грн (0,3$).
Купил его, разобрал старую сгоревшую энергосберегающую лампу (там по окружности где место соединения аккуратно поддеваем ножем), откусил кусачками схему, подпаял новые провода от патрона старой лампы, залудил провода и прикрутил их к контактам патрона.
Вставил патрон в цоколь лампы (Е27) и прикрутил внутри проволокой и замотал изолентой.
Вот что получилось :-), для подъезда вполне покатит, главное все надежно затянуто и заизолировано.




P.S. весь процесс сборки не фоткал, а уже как сделал решил выложить в блог, но в принципе все просто
Поделиться с друзьями:
nemcd.com
Основы Mid-Side записи / Habr
Когда большинство людей думают о стерео-записи, первое, что им приходит в голову — это подобранная пара микрофонов, расположенных в совпадающей (XY) системе. Обусловлено это тем, что такой способ позволяет максимально реалистично повторить пару человеческих ушей.Но в то время, как стереопара является самым очевидным методом, это не единственный игрок на поле стерео-записи. Техника Mid-Side выглядит немного сложнее, но она имеет ряд преимуществ перед обычной подобранной парой. Если вы никогда не слышали о MS-записи, или всегда боялись попробовать, то все это время вы упускали серьезное оружие в вашем звукозаписывающем арсенале.

MS-система, состоящая из AKG 414 в качестве «side»-микрофона и Audio Technica 4051 в качестве «mid»-микрофона.
Больше, чем Вы слышите
Традиционная XY-запись повторяет положение наших ушей. Как и человеческий слух, микрофоны в системе XY опираются на временную задержку в несколько миллисекунд между каналами для локализации звука в стерео-поле. Это достаточно простая концепция работает хорошо до тех пор, пока оба микрофона подобранны и равномерно распределены для получения точного звукового образа.
Одна из слабых сторон такой техники это то, что после записи остается мало возможностей для изменения стерео-изображения. В некоторых случаях прослушивание трека в моно может привести к противофазе сигналов.
MS-техника предоставляет вам гораздо больше контроля над шириной стерео-поля, чем другие, и позволяет внести изменения в любое время после записи.
Mid-Side совсем не новое понятие. Оно было разработано инженером EMI (британская медиагруппа, одна из крупнейших звукозаписывающих компаний мира — прим. переводчика) Аланом Блюмлейном, пионером стереофонического и объемного звука. Блюмлейн запатентовал технику в 1933 году и использовал её на некоторые из самых ранних стереофонических записях.
Записи микрофонами по MS-технологии широко используется в трансляции, в значительной степени потому, что правильно записанные треки всегда моно-совместимы. MS также популярна как техника для студийной и концертной записи, и ее удобство и гибкость делают её хорошим выбором для записи живого звука.
Что требуется
В то время, как XY-запись требует подобранной пары микрофонов чтобы создать согласованный образ, в MS записи часто используется два совершенно разных микрофона, или используются подобные микрофоны, установленные на различные характеристики направленности.
«Mid»-микрофон (центральный) обращен к центру источника звука. Как правило, это будет микрофон с кардиоидной или гиперкардиоидной диаграммой (хотя в некоторых вариациях техники используют ненаправленную или двунаправленную «восьмерку»). К «side»-микрофону (боковому) требования более жесткие: он должен иметь направленность строго в виде «восьмерки». Этот микрофон повернут на 90 градусов от оси источника звука. Оба микрофона следует размещать как можно ближе, как правило, один над другим.
Как это работает
Это не редкость для музыкантов быть запуганными сложностью MS-техники, и я видел, как глаза не одного человека тускнели от объяснений. Но в своей основе методика такой записи не так уж и сложна. Концепция заключается в том, что «mid»-микрофон выступает в качестве центрального канала, в то время как каналом «side»-микрофона создается атмосфера и направление путем сложения или вычитания информацию с любой стороны.
Двунаправленная «восьмерка» «side»-микрофона, повернутая на 90 градусов от источника, принимает окружающие и реверберированные звуки со стороны сцены. В результате того, что это «восьмерка», мы получаем две стороны с разностью фаз в 180 градусов. Другими словами, положительный сигнал на одной стороне диафрагмы микрофона создает равный ему отрицательный на другой стороне. Фронтальная сторона микрофона, обычно представляемая как плюс (+), направлена в левую сторону, в то время как задняя часть, или минус (-), указывает вправо.
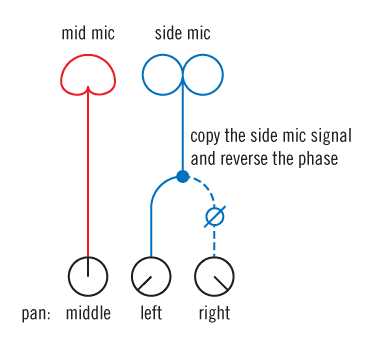
Поток сигналов при MS-записи.
Далее сигнал от каждого микрофона записывается в свой трек. Однако, для того, что бы услышать надлежащий стерео-эффект при прослушивании записи, треки должны быть матрицированы и декодированы.
Итак, вы записали только два канал аудио (центральный и боковой), и следующим шагом будет разделение бокового сигнала на два отдельных канала. Это может быть сделано либо в программном обеспечении вашей DAW (Digital Audio Workstation — прим. переводчика), либо при помощи аппаратного микшера путем переноса «side»-сигнала на два канала, и инвертированием фазы одного из них. В результате получаем два канал, представляющих именно то, что обе стороны вашего микрофона «слышали».
Теперь у вас есть три канала записанного аудио — центральный канал и два боковых канала, которые должны быть сбалансированы для воссоздания стерео-изображения. (Вот где это все становится немного запутанным, так что держитесь крепче.) MS-декодирование работает по тому принципу, что называется «сумма-разность»: добавим один из боковых сигналов — плюс (+) — к центральному сигналу для суммы, а затем вычтем другой боковой сигнал — минус (-) — из центрального сигнала для разности.
Если вы еще не уснули, то вот вам математическая формула:
Mid + (+Side) = left channel
Mid + (-Side) = right channel
После этого, если вы послушаете только центральный канал, то получите моно сигнал. Включите два боковых канала, и вы услышите стерео. А вот самое крутое — ширину стерео-поля можно изменить варьируя количество бокового канала в миксе!
Почему это работает
Инструмент на «мертвой точке» (0 градусов) создает звук, поступающий в «mid»-микрофон непосредственно по оси. Но в то же время этот звук попадает в нулевую точку «side»-микрофона. Конечный сигнал в равной мере идет в левые и правые шины микшера и громкоговорители, в результате к центру изображения.
Инструмент, расположенный на 45 градусов влево, создает звук, который попадает в «mid»-микрофон и одну из сторон «side»-микрофона. Из-за того, что фронтальная сторона «side»-микрофона направлена влево, звук вызывает положительную полярность. Эта положительная полярность в совокупности с положительной полярностью «mid»-микрофона в левом канале приводит к повышенному уровню на левой стороне звукового поля.
Между тем, на правом канале бокового микрофона, тот же сигнал вызывает сдвинутый по фазе сигнал отрицательной полярности. Эта отрицательная полярность в сочетании с сигналом среднего микрофона в правом канале приводит к понижению уровня справа.
Инструмент, расположенный на 45 градусов вправо, создает противоположный эффект, увеличивая сигнал на правой стороне при одновременном снижении его слева.
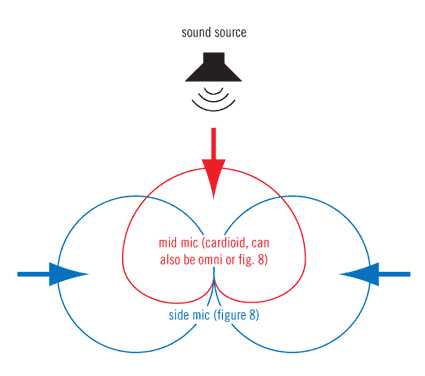
Средний микрофона выступает в качестве центрального канала, в то время как сигнал бокового микрофона создает стерео атмосферу.
В чем преимущество?
Одно из самых больших преимуществ MS-записи является гибкость, которую она предоставляет. Так как стерео изображение находится в прямой зависимости от количества сигнала, поступающего в сторону бокового канала, повышение или снижение соотношения среднего и боковых каналов делает стерео-поле шире или уже. Результатом является то, что вы можете изменить звук вашей стереофонической записи после того, как она уже была записана, что было бы невозможно с использованием традиционной XY-микрофонной записи.
Попробуйте поэкспериментировать с этим — слушайте только средний канал, и вы услышите прямой, монофонический сигнал. Теперь опустите уровень среднего канала и в то же время поднимите уровни боковых каналов. Как только повысятся боковые сигналы и понизится центральный, вы заметите, что стерео становится более широким, а центр отодвигается дальше от вас. (Полное удаление среднего канала приведет к сигналу, являющегося по большей частью звуком атмосферы комнаты — полезно для эффектов, но не более того.) Начав только с центрального канал и постепенно добавляя боковые, вы придете к созданию правильного стерео-изображения трека.
Еще одно большое преимущество MS-техники является то, что она обеспечивает истинную совместимость с моно. Поскольку два боковых канала компенсируют друг-друга, когда вы переключите микс в моно, то останется только центральный «mid», предоставляя вам идеальный монофонический сигнал. А так как боковые каналы также содержат большую часть атмосферы комнаты, переключение микса в моно исключает этот звук, в результате чего получаем микс с повышенной четкостью. Хотя большинство XY-записей моно-совместимы, вероятность подавления фаз больше, чем при MS-записи. Это одна из причин, по которой MS-технология всегда была популярна в мире вещания.
Другие возможности
Хотя большинство MS-записей производятся с использованием кардиоидного микрофона в качестве «mid», его замена может привнести некоторые интересные эффекты. Попробуйте использовать микрофон с ненаправленной диафрагмой для резкого возрастания «просторности» звучания и расширения диапазона низких частот.
Эксперименты с различными комбинациями микрофонов также могут иметь значение. По большей части оба микрофона должны быть крайне схожи в своем звучании. Это особенно важно, когда источник звука достаточно большой, как, например, пианино или хор, потому что каналы обмениваются информацией о панорамировании; в ином случае качество тона будет меняться в стерео-поле. Для небольших источников, таких как акустическая гитара, соответствие микрофонов менее важно. При меньших источника проще экспериментировать с разными микрофонами. Например, попробуйте более ярко звучащую сторону микрофона, что бы окрасить стерео-картину и сделать ее более просторной.
Как вы видите, в Mid-Side записи есть куда больше, чем то, что слышит ваше ухо. Даже если в теории эта техника выглядит устрашающей, на практике вы найдете ее невероятно полезной для достижения полного контроля над стерео-полем в ваших записях.
Примеры
habr.com
Образование (веб 2.0)
Уважаемые специалисты Управлений образования, директора и завучи!
В разделе меню
Мой кабинет/Мониторинг качества услуги опубликован предваритель…
Уважаемые специалисты Управлений образования, директора и завучи!
В разделе меню Мой кабинет/Мониторинг качества услуги опубликован итоговый отчет о работе школ за…
Уважаемые специалисты Управлений образования, директора и завучи!
В разделе меню Мой кабинет/Мониторинг качества услуги опубликован предварительный отчет о работе …
Вниманию пользователей!
В пятницу
01.11 с 08:00 до 11:00 в связи с проведением технических работ портал будет недоступен. Приносим извинения за доста…
«Образование web2.0»
Наш Портал объединяет школы разных регионов России в единую образовательную сеть.Учителя ведут в системе электронные журналы своих школ. Ученики и родители смотрят расписание занятий, домашние задания и оценки. Все участники общаются между собой в рамках безопасной социальной сети, ведут блоги и участвуют в увлекательных конкурсах, которые мы регулярно проводим на Портале.
Присоединяйтесь к нам!
Мы будем рады видеть вас на страницах Портала «Образование web2.0»!
Подключиться
Автономная некоммерческая организация
«Акселератор социально-культурных проектов»
|
На площадке Портала с 2009 года регулярно проводятся некоммерческие культурные мероприятия и реализуются социально-значимые проекты для школьников, их родителей и учителей края.
За период с 2010 по 2016 год было организовано и успешно проведено порядка 50 мероприятий при содействии и поддержке Министерства образования и науки Пермского края и других партнеров. Ежегодно в проектах, проводимых на портале, принимают участие около 1500 человек, при этом: 75% из них – школьники Пермского края, 10% – их родители и 15% – учителя.
В 2016 году для реализации некоммерческих проектов, в том числе, на Портале, было решено создать АНО «Акселератор социально-культурных проектов» (АНО «АСП»). |
 |
Предметом деятельности АНО «АСП» является предоставление услуг по организации, реализации и оказанию содействия в реализации социально-значимых проектов в сфере культуры, физической культуры и спорта, иных сферах.
Целями деятельности АНО «АСП» являются:
- Поддержка и популяризация научно-технического творчества, образования и просвещения, духовно-нравственного и патриотического воспитания, всестороннего развития личности.
- Популяризация изучения и сохранения культурного и исторического наследия, памятников культуры и истории, традиций и самобытности, создание новых конструктивных форм досуга.
- Формирование экологической культуры, пропаганда экологических знаний в области защиты и охраны окружающей среды, защиты животных, поддержка благоустройства и озеленения территории, развитие познавательного и экологического туризма.
- Пропаганда здорового образа жизни, укрепление институтов семьи, поддержка и создание условий для развития физической культуры и спорта, профилактика социально опасных форм поведения.
- Поддержка и продвижение ценностей и практики благотворительности, добровольчества, волонтерства.
|
Контактная информация.
Руководитель проектов — Елена Игоревна Юрьева + 7 (342) 238-53-00 (1071)
Приглашаем стать нашим партнером и участвовать в совместных проектах, направленных на организацию внешкольного досуга детей учебных заведений и центров дополнительного образования, а также родителей и учителей. Прошедшие мероприятия |
Отзывы и благодарности
На портале «Образование web 2.0» вы сможете не только узнать свои оценки, посмотреть расписание уроков, домашнее задание и темы пройденных уроков, но и познакомиться и подружиться с вашими сверстниками из Пермского края и других регионов России.
Простые в использовании социальные сервисы позволят вам вести личный блог, создавать сообщества по интересам, добавлять файлы и фотографии, участвовать в разнообразных интересных конкурсах.
Портал сообщит о важных событиях и изменениях в жизни класса, школы, территории и региона.
Электронный дневник Вашего ребенка, представленный на портале «Образование web 2.0», в отличие от его бумажного аналога, всегда доступен, предоставляет больше информации в наглядной и понятной форме:
— выписки всех оценок с комментариями педагога
— рейтинг учащегося
— точные данные о посещаемости каждого урока
— темы уроков
— сведения о домашнем задании и необходимом времени для его выполнения.
Вы сможете непосредственно общаться с преподавателями Вашего ребенка, получать консультации высококвалифицированных специалистов (он-лайн или в блогах) различных образовательных учреждений по всей России, узнавать новости образования класса, школы, вашей территории, края.
Дневник Вашего ребенка станет для Вас доступным через сеть Интернет в любое удобное для Вас время – дома или на работе, с компьютера, ноутбука или мобильного телефона.
Портал «Образование web 2.0» поможет вам накапливать свой индивидуальный педагогический опыт в виде «копилки» уроков, методических материалов, файлов и другой полезной для обучения информации. Вы всегда будете знать своё расписание и учебную
нагрузку, сможете отследить прохождение программы, общаться напрямую с учениками и родителями, выстраивать индивидуальные траектории обучения для детей, эффективно работать с классом, используя современные интерактивные технологии.
Вы сможете обмениваться опытом и знаниями с ведущими педагогами Пермского края и других регионов России, участвовать в системе совместной подготовки к урокам, а так же в педагогических конкурсах.
Данные за предыдущие учебные года хранятся
на специальных узлах http://2009.web2edu.ru/, http://2010.web2edu.ru/ и http://2011.web2edu.ru/,
http://2012.web2edu.ru/, http://2013.web2edu.ru/,
http://2014.web2edu.ru/,
http://2015.web2edu.ru/, http://2016.web2edu.ru,
http://2017.web2edu.ru. В архивные копии перенесены сведения о текущей и итоговой
успеваемости, расписании, заменах уроков. Для просмотра информации нужно авторизоваться. В архивную копию перенесены только сведения о текущей и итоговой успеваемости, расписании, заменах
уроков за 2008-2009, 2009-2010, 2010-2011, 2011-2012, 2012-2013, 2013-2014, 2014-2015 уч. года. Читать
подробнее…
О безопасном поведении детей в сети Интернет подробнее…
|
Карпович Светлана Ирековна
|
|||
|
Серова Наталья Сергеевна
|
|||
 |
Грабко Ольга Александровна
|
||
|
Гаранин Евгений
|
|||
|
Попова Марина Николаевна Подробнее… |
|||
|
Мальцева Татьяна Евгеньевна Подробнее…
|
|||
| Все отзывы | |||
| Мы будем рады опубликовать Ваши отзывы о портале. Пожалуйста, присылайте Ваши отзывы вместе с информацией о себе и фотографией на электронный адрес [email protected]. | |||
Ваша школа еще не участвует в проекте?
Вы можете зарегистрировать школу несколькими способами:
1. Отправить заявку с портала, заполнив все обязательные поля отмеченные звездочкой.
2. Написать письмо на [email protected] или отправить письмо с портала, в тексте письма обязательно указать регион, населенный пункт, наименование школы, ФИО директора и контактный телефон.
3. Связаться с нами по телефону 8 800 300 4444 или (342) 2 385 280
Как организовать работу? С чего начать?
Вы зарегистрировали школу? Далее действуйте по алгоритму!
Возникли вопросы? Посмотрите, может быть мы уже ответили на них!
Предлагаем вам принять участие в бесплатных мастер-классах, посвящённых введению электронных образовательных услуг!
Дорогие друзья!
Для вас в разделе Интерактив/Мастер-классы работают постоянные Мастер-классы:
1.
Ознакомление с Ролями пользователей портала «Образование 2.0»,
2.
Организация и продвижение в школе электронных услуг,
3.
Работа с родителями с использованием возможностей портала «Образование 2.0»
4.
Представление актуальных it-решений для образования
5.
Представление автономного приложения для работы с электронным журналом web2edu.ru
Мы вас ждём! Регистрируйтесь! Подключайте школу! Звоните 8 800 300 4444 или (342) 2 385 280!
Вы можете познакомиться с функциями рабочих мест ролей Ученика и Родителя, Учителя-предметника, Классного руководителя, Заведующего учебной частью и Директора, для этого щелкните по одной из ссылок. Логин и пароль одинаковые.
* Обращаем Ваше внимание, что под демо-пользователями невозможно изменение данных, Система будет сообщать об ошибке при каждой попытке сохранения любого объекта.
web2edu.ru
