Что такое полигоны в графике: HTTP 429 — too many requests, слишком много запросов

3D в играх: Полигоны | StopGame

3D в играх. Часть 2

Полигоны
Как мы выяснили в прошлой части, современные трехмерные компьютерные игры строятся на основе полигонов. Но, что же это за зверь такой?

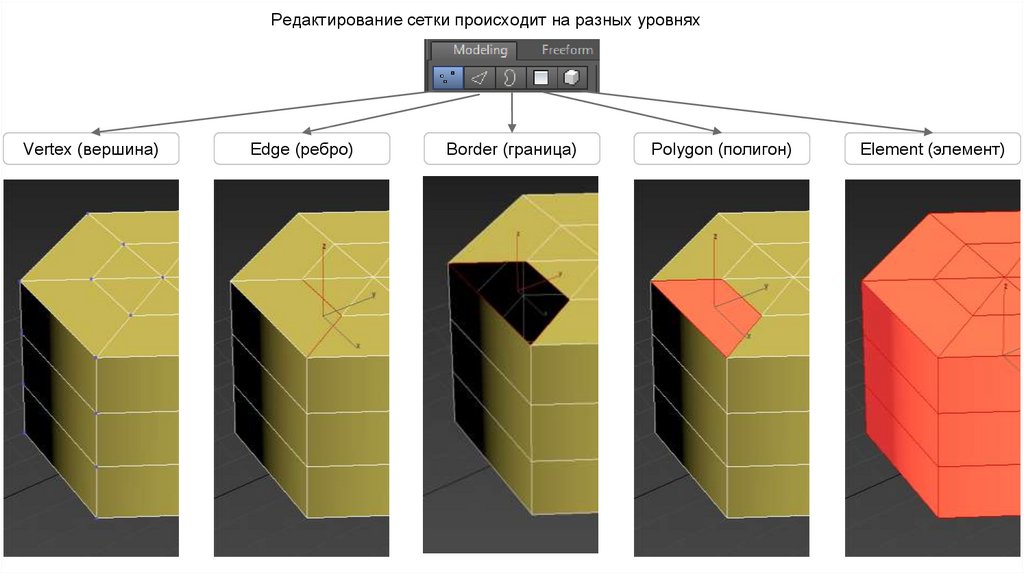
Полигон (Polygon) – это плоскость в евклидовом пространстве. Пространство имеет размерность три, соответственно, имеются три координаты: X, Y, Z. Условно их можно обозвать как длина, высота и глубина. В программном обеспечении для 3D нет единого стандарта относительно, так сказать, ориентации данных координат, хотя, как правило, координата X параллельна условном горизонту, т.е. это длина, а вот условной высотой может быть как Y так и Z. Соответственно, условной глубиной может быть как Z, так и Y. Но нам это не столь суть важно, примем для последующего материала представление, показанное ниже.

У полигона есть вершины, минимум три, максимум, теоретически, бесконечность. Практически максимум – много. Но в играх используются треугольные полигоны, т.

е. полигон имеет три вершины. Почему именно три? Через три точки в пространстве можно провести только одну плоскость, что упрощает расчеты и позволяет избежать искажений (артефактов) на итоговой картинке связанных с тем, что вершины полигона могут лежать не в одной плоскости.

Однако в программах трехмерного моделирования принято пользоваться 4-х угольными полигонами, а вот 5-ти и больше, как правило, под запретом. Поэтому при моделировании приходится следить за тем, чтобы все 4 вершины полигона были в одной или почти одной плоскости. А как же игры? спросите вы. Полигон с 4-мя вершинами математически очень просто превратить в два треугольных с двумя общими вершинами, что и делается автоматически при экспорте в игровой движок.

На рисунке ниже показаны треугольный полигон и четырехугольный, условно разделенный на два треугольных. На изображении это прямоугольный треугольник и прямоугольный параллелограмм, но по факту полигон может иметь различные длины сторон, соответственно, и различные углы между ними. Хотя стараются, по возможности, все стороны делать приблизительно одинаковыми, это называется равномерная полигональная сетка.

Почему сетка? Из полигонов создаются трехмерные объекты для игр (и не только), и если рассматривать все эти полигоны издалека включив отображение сторон полигона, они же ребра, то все это похоже на сетку.

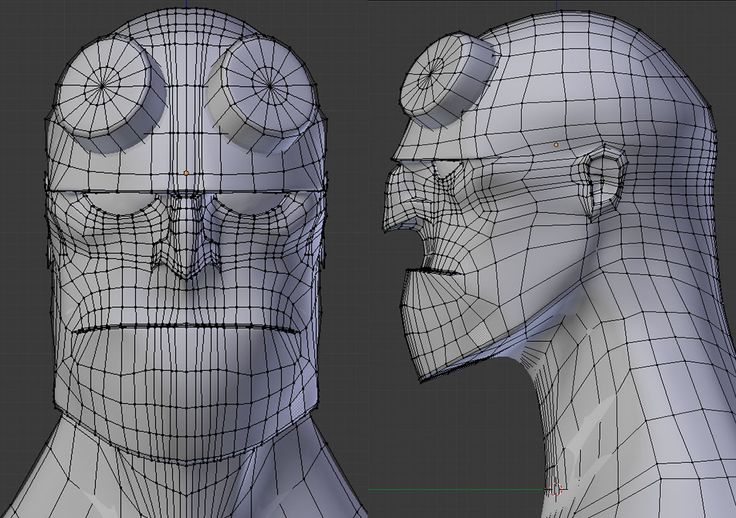
Вообще, полигон – это то, чего на самом деле не существует, это всего лишь математика. У него нулевая толщина. Это координаты трех (для игр, далее будем говорить только о треугольных полигонах, если не будет указано иное) точек в трехмерном пространстве. И то, как отображать эти несуществующие полигоны, — зависит исключительно от той или иной компьютерной программы. Как правило, существуют три основных вида отображения: каркасная сетка, полигональная сетка, «чисто» полигональное представление. На рисунке ниже даны все три вида.

При моделировании, тестировании и т.п. для закрашивания плоскости между вершинами полигона используется произвольный цвет, но зачастую это так называемый сермат, RGB 128,128,128.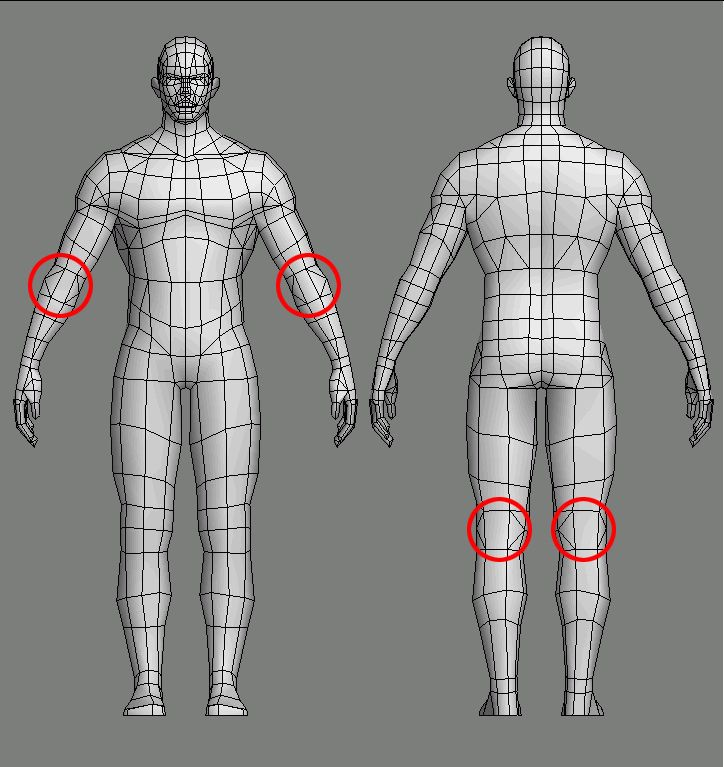

На нем удобно тестировать, в частности, освещение. Да и однородная заливка, в отличии от полновесных текстур, использует не так много ресурсов компьютера.

Приведенный выше рисунок показывает как, на самом деле, с помощью плоских поверхностей создаются объекты практически любой формы. Правило тут простое: чем меньше каждый полигон, тем более точно можно передать форму исходного объекта. Это как с мозаикой, про которую разговор был в первой части. Но и увеличивать до бесконечности количество полигонов тоже нельзя, так как это сказывается на производительности, ведь компьютеру желательно не менее 30 раз в секунду пересчитать положение каждой, по крайней мере видимой зрителю, вершины полигона. Но и эти расчеты лишь малая часть того, что видеокарта в сотрудничестве с ЦП делают для расчета финальной картинки. Но об этом мы поговорим в следующих частях.

Кроме координат вершин есть у полигона такое свойство как нормаль. Это вектор, перпендикулярный одной из сторон плоскости полигона. Так как это вектор, то у него есть направление. Это направление указывает лицевую сторону полигона, вернее его начало находится у лицевой стороны полигона. Нужна нормаль для наложения текстур и расчета освещенности. Так же хочу заметить, что математически полигон не имеет никакого отношения к тому, как он выглядит, т.е. к текстурам. Полигон отдельно, текстуры – отдельно.

Так вот, та сторона, из которой «выходит» вектор нормали — и определяет лицевую сторону полигона, поэтому с противоположной стороны полигон прозрачен при визуализации, вернее обратной стороны просто не существует. Именно поэтому когда игровой персонаж из-за некорректных коллизий проваливается сквозь текстуры, то почти все сверху кажется полупрозрачным – текстур, вернее обратной стороны у полигона не существует.
Ниже скриншот из игры Batman Arkham Knight.

То же можно наблюдать, если попасть туда, куда игровой персонаж попадать не должен по задумке разработчиков: за уступы скал, в закрытые помещения и т.

п. И это не баг игрового движка, это его особенность, ну, и недосмотр при тестировании (или разработчики не отреагировали должным образом на отчет тестировщиков). Необходима такая особенность для оптимизации расчетов итоговой картинки, или, по-другому, рендеринга. Ведь совсем незачем тратить вычислительные ресурсы на то, что никто никогда увидеть не должен.

Внимательный читатель может спросить: а как же быть в том случае, если игровой персонаж должен зайти в помещение? Тогда необходимо, как и в реальном здании, придавать стенам (потолку, крыше, дверям и т.д.) толщину с помощью двух полигонов у которых нормали смотрят в противоположные стороны.

Ниже показан фрагмент модели здания со стеной, имеющей реальную толщину. Синим показано направление нормали у полигонов.

Для совсем тонких предметов, таких как лист бумаги, применяется другой подход и зависит он от конкретного игрового движка. Например, может применяться специальный двухсторонний материал или отключаться параметр Backface culling, и в этом случае объект будет выглядеть одинаково с обеих сторон.

(Подробнее про Backface culling можно почитать тут: Полигоны, свободная камера и MGS 5)

Теперь поговорим о том, какие бывают трехмерные полигональные модели.

3D модели принято делить на низкополигональные (low poly) и высокополигональные (high poly). Как несложно догадаться – разница в количестве полигонов, причем разница не абсолютная, а, как и все в нашем мире, относительная.

Высокополигональной можно назвать модель с самодостаточной геометрией, т.е. когда даже мелкие детали (в разумных, конечно, пределах) смоделированы с помощью полигонов и при этом модель выглядит достаточно правдоподобно даже без текстур. Непосредственно в играх high poly модели, как правило, не применяются, однако они необходимы в процессе разработки 3D игры, о чем будет рассказано ниже.

Высокополигональные модели применяются для статического рендеринга, например интерьерной визуализации или предметной, когда необходимо фотореалистичное качество и большие разрешения итоговой картинки. Для получения такого изображения используются специальные программы рендеринга и просчет одного кадра может занимать несколько десятков часов, поэтому в играх это неприменимо.

Низкополигональные модели применяются в основном в играх или для анимации, когда визуальный реализм не имеет первостепенного значения. Есть два основных способа получения низкополигональной модели: непосредственное моделирование с прицелом на малое количество полигонов или упрощение высокополигональной модели. То же справедливо и для high poly моделей (если не брать в расчет 3D сканирование): их получают путем усложнения и добавления полигонов низкополигональной модели, либо моделируют сразу из расчета максимально необходимого количества полигонов. Какой подход применятся в том или ином случае зависит от многих факторов, как то: геометрии самой модели, применяемого программного обеспечения, наличия похожих моделей, принятого в студии-разработчике порядка разработки, предпочтений 3D-художника и т.п.

Хочу особо обратить внимание на то, что разделение на high poly и low poly очень и очень относительно. Зависит от многих факторов, и одна и та же модель может быть как низкополигональной, так и высокополигональной. Например, для игры для ПК была разработана высокополигональная модель персонажа, затем из нее получили низкополигональную, условно, уменьшив количество полигонов в два раза. А позже решили портировать игру на мобильные устройства. И количество полигонов, опять же, условно, для этого сократили в четыре раза по сравнению с изначальной моделью, или в два раза по сравнению с моделью для ПК-версии игры. Ведь мобильные устройства мало того, что не такие мощные, как ПК, так еще и размер экрана не позволяет различить мелкие детали, поэтому такая высокая детализация, как для полноразмерного монитора, там попросту не нужна.

Ниже показаны сферы одинакового диаметра с различным количеством полигонов.

Да и с каждым новым процессором, каждой новой видеокарточкой мощность компьютерного железа растет, соответственно, и в играх получается отображать в кадре все больше и больше полигонов без ущерба производительности.

Ниже представлена эволюция полигональной Лары Крофт.

Как же получают 3D модели? Традиционно для этого используется полигональное моделирование в специальных программных пакетах, как то: 3ds Max, Maya, Cinema 4D и т.п. В последнее время к разработке также подключают программы для так называемой трехмерной лепки, к примеру ZBrush и 3D-Coat. Ну, и с развитием технологии 3D сканирования, модели получают путем этого самого сканирования с последующей оптимизацией полигональной сетки.

Если используется традиционное полигональное моделирование, то 3D художнику необходимо от чего-то отталкиваться. Для этого используются так называемые референсы, или, по-другому, изображения того, что необходимо смоделировать. Это могут быть фотографии (для реальных предметов или персонажей), концепт-арты (для вымышленных), или даже существующие объекты. К примеру, необходимо смоделировать существующие кубики Lego. Самая в данном случае хорошая идея – иметь их под рукой и моделировать, непосредственно вертя в руках эти самые кубики.
Ниже изображение референса и 3D модели (без текстур).

Теперь вернемся к вопросу: а зачем при разработке 3D игры иметь в наличии сразу две модели одного и того же объекта — high poly и low poly? Высокополигональная модель непосредственно в игре использоваться не будет, но она необходима для такого важного процесса, как запекание текстур. Так называют подготовку целого ряда текстур или, как их еще называют, карт. Это обычные файлы изображений (с необычными, на первый взгляд, рисунками в них) цель которых как можно реалистичнее представить модель в игре и взять на себя, так сказать, часть геометрии. По сути – это создание 3D иллюзии там, где добиться этого полигонами сложно, неподъемно по производительности или просто нецелесообразно.

Возьмем, к примеру, старую доску. В ней может быть множество трещин и мелких сколов. В реальности это перепад высот (или глубин) материала самой доски. И, по-хорошему, полигоны также должны повторять эти перепады. Но тогда модель может оказаться настолько высокополигональной, что никакое железо не потянет это количество полигонов.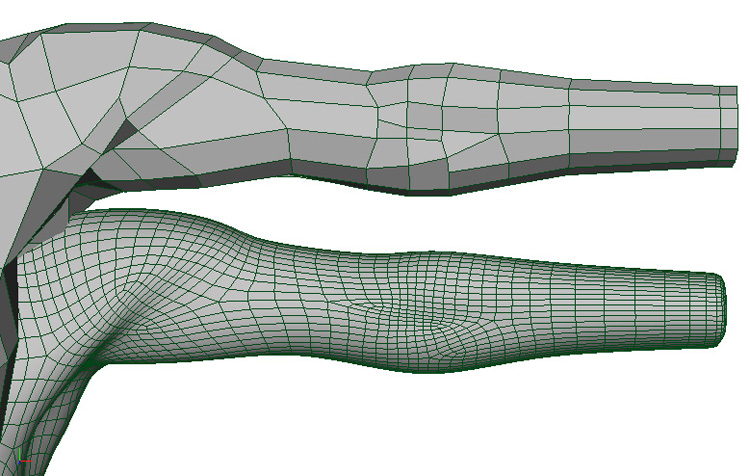 Поэтому для начала моделируют как можно более подробную высокополигональную модель этой самой доски, а затем с помощью специальных программ генерируют (запекают) карты высот, затенения и т.п. для имитации этих самых трещин и сколов на низкополигональной модели.

Ниже упрощенно схематически показано как смешивание запеченных с high poly модели карт, в сочетании с текстурой дерева, в результате дает реалистичное изображение.

Ведь как мы различаем эти самые трещинки и сколы? По изменению яркости и цвета текстуры дерева благодаря тому, что свет по-разному отражается от неровностей поверхности, а кое-где и отбрасывает тень. К тому уже, в трещинах, как правило, накапливается грязь и т.п. Все это и позволяет нам отличить старую древесину от новой. Вот эти эффекты и запекаются в файлы изображений. Такой прием позволяет создавать довольно реалистичные объекты с использованием значительно меньшего количества полигонов. При отображении объекта в игре эти карты накладываются друг на друга по определенным алгоритмам, что и создает иллюзию наличия геометрии, которой на самом деле то и нет.

Правда, тут есть один недостаток: эффект лучше всего действует когда наблюдатель расположен под углом 90° относительно полигонов с такой вот имитацией дополнительной геометрии. С уменьшением или увеличением угла обзора «обман» становится виден все отчетливее и отчетливее. Но это неизбежная плата за возможность приблизить картинку к реализму, не превратив игру в неиграбельную.

Это мы забежали немного вперед, затронув тему текстур, но без этого трубно было бы объяснить необходимость на один игровой объект делать как минимум две модели.

Если уж мы говорим про 3D в играх, то следует обязательно упомянуть такую технологию, как LOD, сокращенно от Level of Detail, она же уровень детализации. Суть ее сводится к тому, что в зависимости от того, насколько тот или иной объект близко располагается от игрового персонажа, или какой процент высоты экрана занимает, то используются модели с различного рода детализацией. Опять же, все ради оптимизации. Чем ближе к виртуальной камере тот или иной объект, тем более детализированная модель подставляется. На практике часто количество таких моделей ограничивается тремя: для переднего, среднего и заднего планов. И обозначаются, как правило: LOD_0, LOD_1, LOD_2. Это все варианты низкополигональной игровой модели.

Различные варианты полигональной детализации могут создаваться как в сторонних программах, так и автоматическими игровыми движками (очевидно, не всеми). Причем автоматически в сторону упрощения геометрии, т.е. загруженный в игровой движок вариант по умолчанию воспринимается как LOD_0. Иногда в играх, особенно с большими открытыми мирами, можно заметить как изначально угловатый и неказистый объект вдруг скачкообразно «похорошел» — это произошла замена на более высокополигональный LOD.

Вот, наверно, вкратце и все про полигоны. Если остались необозначенные или нераскрытые моменты – пишите про это в комментариях.

По идее, далее необходимо продемонстрировать этот самый процесс полигонального моделирования, дабы наглядно показать, как это делается. И пример должен быть не очень простой, ради показа хотя бы нескольких приемов моделирования, но и не очень сложный, чтобы не нагонять сон на зрителя. Я думал-думал над предметом моделирования и пришел к выводу, что модель керосиновой лампы неплохо впишется в данную концепцию. Но, дабы не утомлять читателя, решил собственно процесс моделирования вынести в третью, или, если хотите, в 2,5 часть повествования, которую надеюсь опубликовать в ближайшем будущем.

А на этом пока все, до новых встреч!

---

Теги

3ds Max polygon трехмерное моделирование текстуры

Новость

Valve собралась дарить по Steam Deck за каждую минуту эфира The Game Awards 2022

Лина Скорич 9 Новость

Хендерсон: студия Splash Damage делает MMO про трансформеров

Андрей Маковеев 2 Первая полоса

Выбираем лучший бесплатный клон Diablo

Кирилл Волошин 45 Рефанд

Ищем хорошие игры

17 Новость

Анонс Amnesia: The Bunker — хоррора-песочницы с аналогом Чужого из Alien: Isolation

Руслан Присекин 26 Видеообзор

God of War: Ragnarök: Последний BOY

Василий Гальперов 94 Истории серии

История серии The Elder Scrolls. Выпуск 1. Заря над Тамриэлем

Иван Лоев 66 Новость

Скоро в Game Pass — LEGO SW: The Skywalker Saga, High On Life, Potion Craft…

Руслан Присекин 1

Основы трёхмерной графики — Полигон

Основы 3D графики Пятница, 02.12.2022, 11:07 | RSS Меню сайта Опрос Полигон — единая величина в моделировании. Как известно, если три или более точек координат заданы в качестве вершин и соединены ребрами, то они формируют многоугольник (полигон), который может иметь цвет и текстуру. Соединение группы таких полигонов позволяет смоделировать практически любой объект. Недостаток полигонального моделирования состоит в том, что все объекты должны состоять из крошечных плоских поверхностей, а полигоны должны иметь очень малый размер, иначе края объекта будут иметь ограненный вид. Это означает, что если для объекта на сцене предполагается увеличение, его необходимо моделировать с большим количеством полигонов (плотностью) даже, несмотря на то, что большинство из них будут лишними при удалении от объекта. Форма входа Block title Block content Календарь «  Декабрь 2022  » Пн Вт Ср Чт Пт Сб Вс       1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 Календарь Block content Babich Alex. FIIT. © 2022

Типы многоугольников — GeeksforGeeks

Многоугольник — это не что иное, как замкнутая фигура (соединенная встык), состоящая из более чем двух отрезков на двумерной плоскости. Слово Polygon состоит из двух слов: первое Poly означает «много», а gons означает «стороны». Многоугольник означает не что иное, как форму, имеющую много сторон. Или, другими словами, многоугольник создается с использованием прямолинейных отрезков, которые соединены друг с другом встык, и эти отрезки называются сторонами многоугольника, а точка называется вершиной многоугольника. Если фигура не содержит сторон и углов, то она не является многоугольной окружностью. Некоторые из полигонов: 

Свойства многоугольника:

• Мера каждого внешнего угла n-стороннего правильного многоугольника будет равна 360°/n.
• Мера каждого внутреннего угла n-стороннего правильного многоугольника будет [(n – 2) × 180°]/n.
• Количество треугольников, образованных соединением диагоналей из одного угла многоугольника, будет n – 2.
• Количество диагоналей в многоугольнике с n сторонами будет n(n – 3)/2.
• Сумма всех внутренних углов n-стороннего многоугольника будет (n – 2) × 180°.

Терминология:

1. Диагонали: Отрезок, соединяющий две непоследовательные вершины многоугольника, называется диагональю. Например, на данном рисунке AC и BD — две диагонали квадрата ABCD.

2. Смежные стороны: В многоугольнике, если две стороны имеют общую вершину, то такие стороны называются смежными сторонами. Например, на приведенном выше рисунке AD и DC являются смежными сторонами.

3. Смежная вершина: В многоугольнике, если две конечные точки или вершина одной стороны, то такой тип вершины известен как смежная вершина. Например, на приведенном выше рисунке вершины A и B являются соседними вершинами стороны AB.

Типы многоугольников:

Существует 4 типа многоугольников:

• Правильный многоугольник: Если все стороны и внутренние углы многоугольника равны или если многоугольник равноугольный и равносторонний, то многоугольник будет известен как правильный многоугольник. Пример квадрат, ромб, равносторонний треугольник и т. д.

• Неправильный многоугольник: Если все стороны и внутренние углы многоугольника имеют разную величину, то такой многоугольник называется неправильным многоугольником. Пример разностороннего треугольника, прямоугольника, воздушного змея и т. д.

• Выпуклый многоугольник: Если все внутренние углы многоугольника строго меньше 180° ^{или если отрезок прямой между двумя точками на границе не выйти за пределы многоугольника, то многоугольник будет известен как выпуклый многоугольник.}

• Вогнутый многоугольник: Если один или несколько внутренних углов многоугольника больше 180° градусов или многоугольник содержит хотя бы один отраженный внутренний угол, то такой многоугольник называется вогнутым многоугольником. Этот многоугольник может иметь по крайней мере четыре стороны.

Углы многоугольника:

В многоугольниках есть два типа углов:

• Внутренний угол: Это угол внутри фигуры, или мы можем сказать, что форма угла внутри многоугольника и сумма внутренних углов многоугольника

Сумма внутренних углов = (n – 2) x 180,

Здесь n – общее количество сторон многоугольника

или

Внутренний угол = 180° – Внешний угол,

или в радианах,

Сумма внутренних углов= = (n – 2)π радиан.

Например:

• Внешний угол: Это угол, образованный стороной и продолжением смежной стороны, а сумма внешних углов многоугольника равна 360 ^или . Сумма внешних углов многоугольника равна

Внешний угол = 180° – Внутренний угол

Если многоугольник имеет n сторон, то

Сумма всех внешних углов = n x 180° – сумма всех внутренних угол

Важные моменты:

• В каждом многоугольнике сумма внешних углов всегда будет 360°.
• Для правильного многоугольника размер каждого внешнего угла = 360° ÷ количество сторон.
• Для правильного многоугольника количество сторон = 360° ÷ размер внешнего угла.

Например:

Классификация многоугольников

Многоугольники классифицируются на основе количества сторон или вершин, которые они имеют. So, some of the polygons are:

Polygon	No. of sides	No. of Diagonal	No. of vertices	Interior Angle
Triangle	3	0	3	60
Quadrilateral	4	2	4	90
Pentagon	5	5	5	108
Hexagon	6	9	6	120
Heptagon	7	14	7	128. 571
Octagon	8	20	8	135
Nonagon	9	27	9	140
Decagon	10	35	10	144
Hendecagon	11	44	11	147.273
Dodecagon	12	54	12	150
Triskaidecagon	13	65	13	158.308
Tetrakaidecagon	14	77	14	154.286
Pentadecagon	15	90	15	156

Треугольники(3-угольник)

Треугольник — это многоугольник, он образован с помощью пересекающихся друг с другом отрезков из трех прямых, поэтому треугольник имеет 3 вершины, 3 ребра и 3 угла. Треугольники делятся на разные типы в зависимости от сторон и углов.

Некоторые свойства треугольника:

• Площадь треугольника: 1/2 × основание × высота
• В треугольнике сумма всех внутренних углов треугольника равна 180 ^o .
• Сторона, противоположная наибольшему углу, является наибольшей стороной треугольника.
• Периметр треугольника равен сумме длин всех трех сторон треугольника.

По сторонам:

• Равносторонний треугольник: Если треугольник имеет все стороны равные и углы равны, то такие типы треугольников известны как равносторонний треугольник.
• Равнобедренный треугольник: Если какой-либо треугольник имеет равные любые 2 стороны и углы, противоположные равным сторонам равны, то такие типы треугольников известны как равнобедренные треугольники.
• Разносторонний треугольник: Если треугольник, у которого все 3 стороны не равны, то такие типы треугольников известны как разносторонний треугольник.

В зависимости от угла:

• Остроугольный треугольник: Треугольник, каждый угол которого меньше 90°, то такой тип треугольника известен как остроугольный треугольник.
• Прямоугольный треугольник: Если любой из трех углов треугольника равен 90°, то такой тип треугольника называется прямоугольным.
• Тупоугольный треугольник: Если какой-либо из углов треугольника больше 90°, то такой тип треугольника известен как тупоугольный треугольник.

Четырехугольники (4-угольники) 

Четырехугольник — это не что иное, как многоугольник, имеющий по крайней мере 4 стороны. Многоугольник формируется путем включения четырех отрезков так, чтобы они пересекались друг с другом в вершинах, образуя 4 или более углов. Пример: Квадрат, Прямоугольник, Параллелограмм, Ромб, Трапеция.

Некоторые свойства четырехугольника:

• Четырехугольник.
• Имеет четыре вершины.
• В четырехугольнике сумма всех внутренних углов равна 360 ^o .

Примеры задач

Вопрос 1. Найдите внешний угол правильного шестиугольника?

Решение: 

Поскольку мы знаем, что шестиугольник имеет 6 сторон, следовательно,

Внешний угол = 360 ^o / n = 360 ^o / 6

Внешний угол = 60 ^o

Вопрос 2. Найдите внутренний угол правильного пятиугольника?

Решение:

Как мы знаем, что Пентагон имеет 5 сторон, поэтому

Внешний угол = 360 ^O /5 = 72 ^O

Угла внутреннего угла = 180 ^O — 72

. о = 108 ^о  

Вопрос 3. Найдите каждый внутренний угол правильного десятиугольника.

Решение : 

Как мы знаем, у десятиугольника десять сторон.

Используя формулу суммы углов, × 180°

= 8 × 180° = 1440°

Поскольку мы знаем, что все внутренние углы правильного десятиугольника равны,

Следовательно, мера каждого внутреннего угла правильного десятиугольника = сумма внутренних углов / количество сторон

Внутренний угол = 1440 / 10 = 144°

Следовательно, сумма внутренних углов десятиугольника равна 1440° и каждый внутренний угол составляет 144°.

Вопрос 4. Найдите значение x на данном рисунке:

Решение:

Поскольку мы знаем, что сумма углов четырехугольника 90 10 8 9 = 1070 8 3600003

so, 55 ^o + 124 ^o + 70 ^o + x = 360 ^o

249 ^o + x = 360 ^o

x = 111 ^o

Вопрос 5.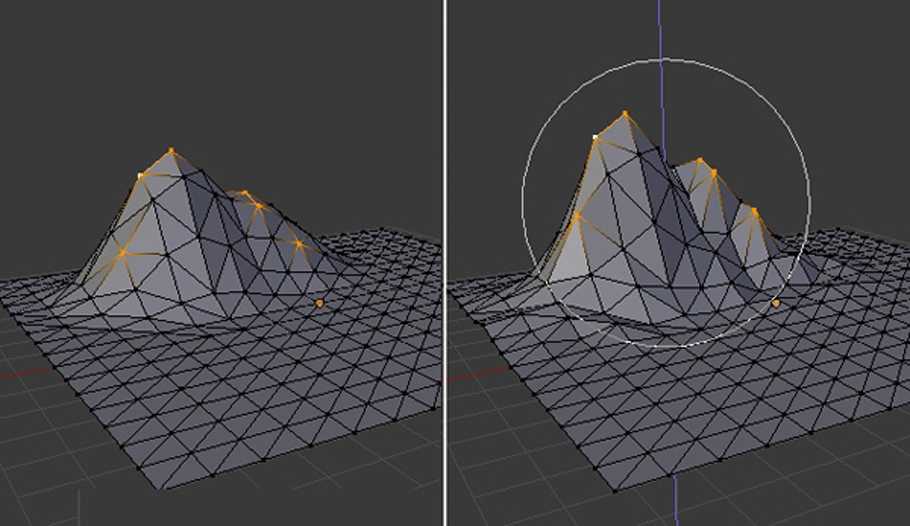 Найдите значение x на данном рисунке:

Решение:

Так как мы знаем, что сумма внешних углов = 360 ^o

Значит, 120 108

х = 360 ^о

245 ^о + x = 360 ^O

x = 360 ^O — 245 ^O

X = 115 ^O

5 Простые факты для мебели. , заказывая 3D-модели продукта, маркетологи не знают, нужны ли им высокополигональные или низкополигональные 3D-объекты. В свою очередь, менеджеры 3D-студий должны точно знать, какой вариант выбирает клиент, чтобы они могли подготовиться к проекту. Но что такое полигоны в 3D-моделировании? Честно говоря, мало кто из непрофессионалов знает об этом.

Из-за незнания терминологии 3D-моделирования маркетологи могут заказать неправильный тип 3D-моделей. В результате готовые 3D-объекты не будут работать по своему назначению. Поэтому им приходится перезаказывать их и тратить дополнительные деньги на новый виток 3D-моделирования.

Чтобы наладить продуктивное сотрудничество со студией 3D моделирования , для начала нужно разобраться, что такое полигоны. Чтобы помочь производителям и маркетологам, мы сузили всю тему полигонального 3D-моделирования до 5 основных фактов, которые им следует знать. Без лишних слов, давайте приступим к чтению!

№1. Многоугольники — это базовые геометрические компоненты 3D-модели

Геометрия многоугольника состоит из прямых ребер и вершин. Образованная плоскость называется гранью, которая обычно представляет собой трехстороннюю геометрическую форму, или «треугольный многоугольник». Также существуют четырехсторонние «четверки» и «n-угольники» с несколькими вершинами. Каждый полигон соединяется с другими полигонами, и вместе они создают полигональную сетку, которая по сути является 3D-моделью. Итак, отвечая на вопрос «что такое полигоны в 3D-моделировании?» мы говорим, что они являются ключевыми компонентами любого 3D-объекта.

Количество полигонов в сетке называется полигоном, а плотность полигонов — разрешением. Те части 3D-модели, в которых много деталей — например, фурнитура, ручки, элементы декора — имеют более высокое разрешение. А большие плоские поверхности, такие как столешница или дверца шкафа, являются низкополигональными секциями меша.

#2. С помощью полигонального 3D-моделирования компьютерные художники могут создавать любые формы

Теперь, когда мы объяснили, что такое полигоны, пришло время поговорить о творческой свободе, которую они предоставляют для этого типа 3D-моделирования. Прежде всего, полигональная сетка может быть любой формы. Даже когда речь идет о сложных конструкциях мебели с изогнутыми поверхностями и резьбой, многоугольники создают идеальную сетку из треугольников и n-угольников, чтобы повторять форму объекта.

Однако даже при такой гибкости специалисты по компьютерной графике стараются избегать создания сверхсложных сеток с миллиардами полигонов. Вместо этого они создают сложные трехмерные объекты, используя меньшее количество полигонов. Таким образом, специалисты по 3D-моделированию могут быть уверены, что в сетке нет выступов полигонов или узлов. Любая ошибка, допущенная на этапе 3D-моделирования, позже проявится в 3D-рендеринге, поэтому компьютерные художники максимально упрощают геометрию.

№3. Каждый полигон и полигональная сетка легко модифицируются 

После того, как сетка готова, разработчики 3D-моделей все еще могут трансформировать ее, манипулируя ее полигонами. Например, вытягивая вершину или ребро, они могут разделить или выдавить грань многоугольника, а также скрутить и растянуть сетку по мере необходимости.

Такие свойства полигональных 3D-моделей позволяют художникам компьютерной графики использовать базовые фигуры, такие как кубы, цилиндры, сферы, в качестве основы. Изменяя вершины многоугольников, они могут лепить из них любую форму. Естественно, что при полигональном моделировании требуются навыки и опыт для создания объектов точных пропорций. Поэтому лучше всего использовать профессиональные услуги 3D-моделирования, чтобы все было сделано на месте.

#4. Существуют высокополигональные и низкополигональные 3D-модели

Так в чем же разница между высокополигональным и низкополигональным 3D-моделированием? Чем больше полигонов состоит из объекта, тем лучше его детализация и качество. Поэтому высокополигональные объекты лучше всего подходят для высокофотореалистичных 3D-визуализаций, таких как рендеринг продуктовых хранилищ и 3D-изображений образа жизни. Для таких визуалов крайне важно качество, ведь они необходимы для печатных журналов и наружной рекламы — билбордов, баннеров, сити-лайтов и т. д.

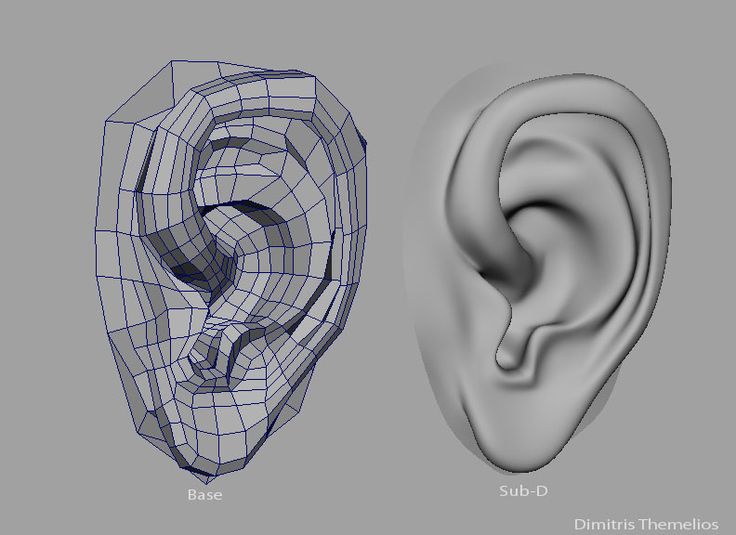
В свою очередь, низкополигональное 3D-моделирование позволяет CG-художникам создавать 3D-объекты для интерактивных CG-решений, таких как 360-градусный обзор, 3D-конфигуратор продуктов , VR/AR-приложения, игры и т. д. Дело в том, что чем меньше полигонов , тем быстрее 3D-объект может быть отображен движком в режиме реального времени. В результате каждый объект выглядит реалистично и плавно перемещается в приложении или движке.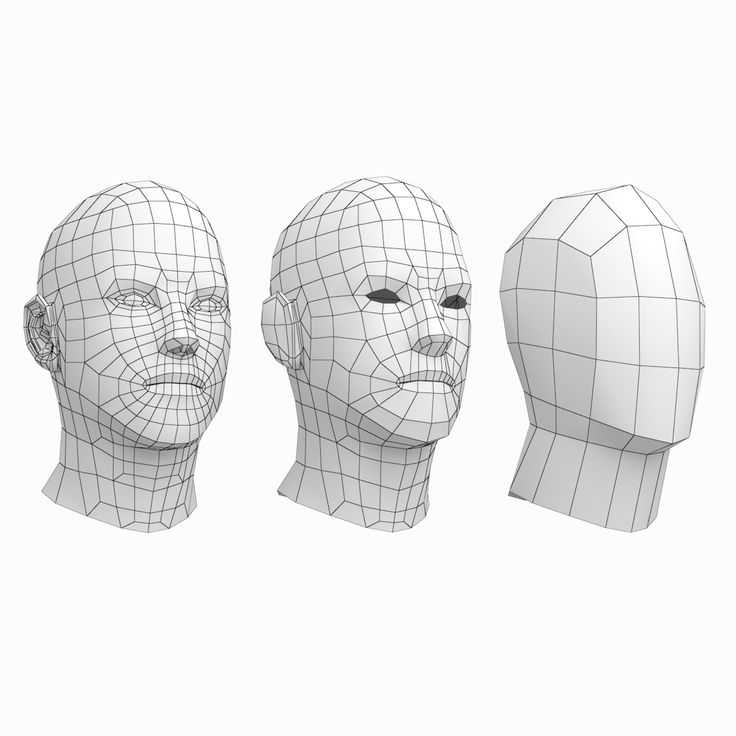

№5. CG-художники часто делают ретопологию для оптимизации 3D-моделей

Что такое полигоны в 3D-моделировании и насколько важно их количество? Пришло время поговорить о ретопологии 3D модели. Ретопология — это оптимизация полигональных объектов, которая позволяет художникам компьютерной графики уменьшить количество полигонов в сетке и преобразовать высокополигональные элементы в низкополигональные. Таким образом, они могут адаптировать высококачественные 3D-модели к игровым движкам, приложениям и конфигураторам 3D-продуктов.

Как мы уже упоминали выше, производителям часто нужны как высоко-, так и низкополигональные 3D-модели для разных задач. Поэтому художники компьютерной графики начинают с создания высокополигональных объектов для высококачественной 3D-рендеринга и 3D-анимации. Затем они ретопологизируют те же 3D-элементы и превращают их в легкие и удобные для рендеринга 3D-объекты для приложений.

Скачайте прайс-лист CGIFURNITURE и узнайте стоимость топовых проектов 3D визуализации разного масштаба!

Посмотреть наши цены

Итак, что такое полигоны в 3D моделировании и как заказать нужный тип 3D моделей? Помните, что количество полигонов и плотность сетки напрямую влияют на качество 3D-элементов.