Четырёхмерное пространство | это… Что такое Четырёхмерное пространство?
ТолкованиеПеревод
- Четырёхмерное пространство
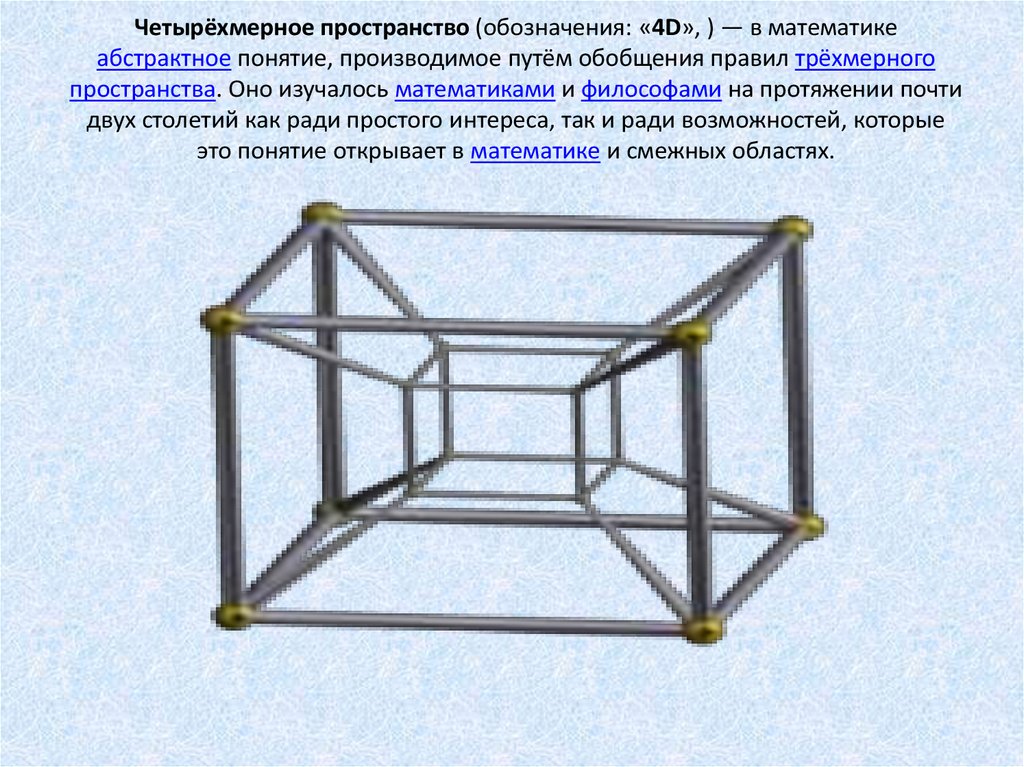
3D проекция тессеракта, простое вращение
Четвёртое измерение, или четырёхмерное («4D») пространство — в математике абстрактное понятие, производимое путём обобщения правил трёхмерного пространства. Оно изучалось математиками и философами на протяжении почти двух столетий как ради простого интереса, так и ради возможностей, которые это понятие открывает в математике и смежных областях.
Алгебраически оно получено путём применения правил векторов и координатной геометрии к пространству с четырьмя измерениями. В частности, вектор с четырьмя компонентами может быть использован для представления позиции в четырёхмерном пространстве.
Это Евклидово пространство, поэтому имеет метрику и норму, и таким образом все измерения рассматриваются одинаково: дополнительное измерение неотличимо от трёх других.В современной физике пространство и время объединены в единый четырёхмерный континуум, называемый пространством Минковского, метрика которого рассматривает временное измерение иначе, чем пространственные измерения. Таким образом, пространство Минковского является псевдоевклидовым, а не евклидовым.
Аналогично 2- и 3-мерным пространствам, скалярное произведение векторов вычисляется по формуле:
Стереографическая проекция тора Клиффорда: множество точек (cos(a), sin(a), cos(b), sin(b)), который является подмножеством 3-сферы.
См. также
- N-мерная евклидова геометрия
- Старшие размерности
- Гиперкуб
Ссылки
- Dimensions — видео-прогулка по математическим размерностям, различные представления многомерных объектов, подробные примечания со ссылками (рус. )
- Эбботт Э., Бюргер Д. Флатландия. Сферландия. (рус.)
- MagicCube 4D 4-мерный аналог традиционного кубика Рубика (англ.)
- Покадровая анимация 4D—3D аналогий (англ.)
- Найти выход из лабиринта в 3Д и 4Д. Удобное управление на клавиатуре. Java (англ.) или для WinXP
- Jenn3D (англ.) — управляемый полет в 3-стереографической проекции 4-политопов, например, тессеракта
- 4D евклидово пространство (англ.)
- 4D Building Blocks — Interactive game to explore 4D space (англ.)
- 4DNav — Простой инструмент для просмотра 4-мерного объекта в четырех 3-мерных проекциях (фр.) использует алгоритм прямолинейного проектирования ADSODA (англ.)
- TeV scale gravity, mirror universe, and … dinosaurs статья Зураба К. Силагадзе из Acta Physica Polonica B (англ.)
- Вики-сборник 4-мерия Гаррета Джонса (англ.)
- Т.Бриггс. Исследование гиперпространства с помощью геометрического произведения (англ.)
Это Евклидово пространство, поэтому имеет метрику и норму, и таким образом все измерения рассматриваются одинаково: дополнительное измерение неотличимо от трёх других.
) Wikimedia Foundation.
2010.
Игры ⚽ Нужен реферат?
- Четырёхкратный залп
- Четырёхтактный двигатель
Полезное
Что такое четырехмерное пространство? — Hi-News.ru
Представление мира в различных измерениях меняет то, как мы воспринимаем все вокруг, включая время и пространство. Думать о разнице между двумя измерениями и тремя измерениями легко, но что насчет четвертого? Важно понимать, что имеют в виду ученые и другие исследователи, когда говорят о различных измерениях: наш мир имеет три пространственных измерения: ширину, глубину и высоту, а четвертым измерением может быть время. Ученые много лет проводят исследования в попытках выяснить что же такое четвертое пространственное измерение, однако по причине того, что наблюдать четвертое измерение мы не можем, доказательства его существования найти очень трудно.
Моделирование движения камеры в четырёхмерном пространстве.
Сколько существует измерений?
Чтобы лучше понимать, на что может быть похоже четвертое измерение, давайте поближе посмотрим на то, что именно делает три измерения трехмерными, и, следуя этим идеям, подумаем о том, что такое четвертое измерение.
Итак, длина, ширина и высота составляют три измерения наблюдаемого мира. Все три измерения мы можем наблюдать благодаря эмпирическим данным, а также органами чувств – такими как зрение и слух.
Определить положение точек и направления векторов в трехмерном пространстве можно вдоль опорной точки. Проще всего представить себе трехмерное пространство как трехмерный куб с тремя пространственными осями, которые определяют ширину, высоту и длину куба. Оси движутся вперед и назад, вверх и вниз, влево и вправо вместе со временем – измерением, которое мы непосредственно не наблюдаем, но воспринимаем. При сравнении 3D и 4D, учитывая наблюдения трехмерного пространственного мира, четырехмерный куб будет Тессерактом – объектом, который движется в трех измерениях, которые мы и воспринимаем и в четвертом, которое е можем наблюдать.
Четырехмерный куб (тессеракт) выглядит так
Еще больше статей о последних открытиях в области теоретической физики и высоких технологий читайте на нашем канале в Яндекс.
Дзен. Там регулярно выходят статьи, которых нет на сайте.
Четырехмерные объекты и тени
Как пишет Sciencing.com, поскольку трехмерные существа отбрасывают тень на двумерную поверхность Куба, это привело исследователей к предположению о том, что четырехмерные объекты отбрасывают трехмерную тень. Вот почему можно наблюдать «тень» в трех пространственных измерениях, даже если непосредственно наблюдать четыре измерения нельзя.
Математик Генри Сегерман из университета штата Оклахома создал и описал свои собственные 4-мерные скульптуры. Точно так же, как трехмерный объект отбрасывает двумерную тень, Сегерман утверждал, что его скульптуры являются трехмерными тенями четвертого измерения. Хотя эти примеры теней не дают прямых способов наблюдения четвертого измерения, они являются хорошим индикатором того, как думать о четвертом измерении.
Фигуры математика Генри Сегермана выглядят так
Математики часто приводят аналогию с муравьем, идущим по листу бумаги, описывая границы восприятия относительно измерений.
Муравей, идущий по поверхности бумаги, может воспринимать только два измерения, но это не значит, что третьего измерения не существует. Это просто означает, что муравей может непосредственно видеть только два измерения и выводить третье измерение через рассуждения об этих двух измерениях. Точно так же люди могут размышлять о природе четвертого измерения, не воспринимая его непосредственно.
Вам будет интересно: Мозг строит странные структуры в 11 измерениях
Четырехмерный куб Тессеракт – это один из примеров того, как трехмерный мир, описываемый x, y и z, может расширяться в четвертый. Математики, физики и другие ученые могут представлять векторы в четвертом измерении, используя четырехмерный вектор, который включает в себя другие переменные, такие как w. Геометрия объектов в четвертом измерении более сложна, так как включает в себя 4-многогранники, которые являются четырехмерными фигурами. Эти объекты показывают разницу между 3D и 4D изображениями.
Существует ли жизнь в четвертом измерении?
То, как выглядели бы существа или жизнь в четырех измерениях, занимало ученых и других специалистов на протяжении десятилетий. В рассказе писателя Роберта Хайнлайна 1940 года «Дом который построил Тим» речь шла о постройке здания в форме Тессеракта. Писатель Клифф Пиковер представлял себе четырехмерных существ как «воздушные шары телесного цвета, постоянно меняющиеся в размерах. Эти существа будут казаться вам разрозненными кусками плоти, точно так же, как двумерный мир позволяет вам видеть только поперечные сечения и остатки мира трехмерного.»
Кадр из мультсериала «Футурама», 15 серия 7 сезона. Перед вами герои в 2D
Четырехмерная форма жизни может видеть вас изнутри точно так же, как трехмерное существо может видеть двумерное со всех сторон.
Джон Нортон из Отдела истории и философии науки Питтсбургского университета считает, что можно прийти к пониманию природы четвертого измерения, задавая вопросы о том, что делает одно -, двух — и трехмерные объекты и явления такими, какие они есть, экстраполируя их в четвертое измерение.
Существо, живущее в четвертом измерении, может обладать таким «стереовидением», описанным Нортоном, чтобы визуализировать четырехмерные образы, не будучи стесненным тремя измерениями.
Однако точно ответить на вопрос о том, существуют ли 4D существа сегодня не может никто. Я полагаю, что даже концепция 4D-пространства ожесточенно обсуждается в физических лабораториях, хотя некоторые теории, такие как Теория струн и М-теория, используют существование нескольких измерений для объяснения нашей Вселенной. Важно также отметить, что биологически 4d жизнь не может существовать. А что вы думаете по этому поводу? Присоединятйесь к обсуждению этой темы в комментариях, а также с участниками нашего Telegram чата.
ВселеннаяНаука физика
Четыре измерения
Четыре измерения| ГЭС 0410 | Эйнштейн для всех | |
Назад на страницу основного курса
Нортон Кафедра истории и философии науки
Университет Питтсбурга
- Одномерный интервал
- Двумерный квадрат
- Трехмерный куб
- Четырехмерный куб: тессеракт
- Стереовидение
- Сводная таблица
- Вместительный вызов
- Запутанный вызов
- Использование цветов для визуализации дополнительного измерения
- Что вы должны знать
Мы уже видели, что нет ничего страшного таинственно о добавлении одного измерения к пространству, чтобы сформировать пространство-время. Тем не менее трудно устоять перед затянувшимся беспокойство по поводу идеи четырехмерного пространства-времени. проблема не в
Но куда нам
поставить четвертую ось, чтобы сделать четырехмерное пространство? Моя текущая цель — показать вам, что в
все таинственное в четырех измерениях пространства-времени. Для этого я брошу
временная часть полностью. Я просто рассмотрю четырехмерный
космос; то есть пространство точно такое же, как наше трехмерное пространство, но с
одно дополнительное измерение. Каково это?
Без всяких усилий я могу визуализировать трехмерное -мерное пространство — и вы тоже можете. Что бы это быть как жить в трехмерном кубе? Чтобы его попросили визуализировать это как просят дышать или моргать. Это легко. Там мы сидим в куб с шестью квадратными стенками и восемью углами. Наш разум позволяет мы парим внутри.
Могу ли я представить, каково было бы жить в
четырехмерный аналог куба, четырехмерный куб или
«тессеракт»? Я не могу представить это с таким же легким
непосредственность. |
Дверь в четвертое измерение открывается.
Одномерный интервал
Одномерным аналогом куба является интервал. Это
формируется путем взятия безразмерной точки и ее перетаскивания на определенное расстояние.
Это расстояние может быть 2 дюйма или 3 фута или что-то еще. Давайте позвоним
расстояние «Л».
Интервал имеет длину L. Он ограничен двумя точками как его грани — две точки на обоих концах интервала.
Двумерный квадрат
Двумерным аналогом куба является квадрат. Это образованный перетаскиванием одномерного интервала на расстояние L в второе измерение.
Квадрат имеет площадь L 2 . Он ограничен гранями
на 4 стороны. Грани — это интервалы длины L. Мы знаем, что их четыре.
их, поскольку его двумерные оси должны быть закрыты с обоих концов гранями.
Итак, у нас есть 2 измерения x 2 грани в каждой = 4 грани. грани вместе образуют периметр длиной 4xL.
Трехмерный куб
Объем куба L 3 . Он ограничен гранями
на 6 сторон. Грани представляют собой квадраты площадью L 2 .
Мы знаем, что есть
6 из них, так как его трехмерные оси должны быть закрыты с обоих концов
лица.
Итак, у нас есть 3 измерения x 2 грани в каждой = 6 граней. грани вместе образуют поверхность площадью 6xL 2 . Рисование изображение трехмерного куба на двумерной поверхности одинаково легко. Берем две его грани — два квадрата — и соединяем углы.
Есть несколько способов сделать рисунок, который соответствует взгляду на куб под разными углами. На рисунке показано два способа сделать это. Первый дает косой обзор; второй смотрит по одной из осей.
Четырехмерный куб: тессеракт
Пока я надеюсь, что вы нашли наши конструкции полностью
безупречный. Следующий шаг в четыре измерения можно сделать одинаково
механически. Мы просто систематически повторяем каждый шаг выше. Единственный
разница в том, что на этот раз мы не можем легко сформировать ментальную картину
что мы строим.
Чтобы сформировать тессеракт, мы берем куб и перетаскиваем его
расстояние L в четвертом измерении . Мы не можем точно представить
как это выглядит, но это примерно так:
Тессеракт имеет объем L 4 . Он ограничен
грани с 8 сторон. Грани представляют собой кубы объема L 3 . Мы знаем
их 8, так как его четыре оси должны быть ограничены
любой конец гранями — две кубические грани на ось. Еще раз, мы не можем
визуализируйте все четыре из этих закрытых измерений. Мы можем в лучшем случае визуализировать
три направления перпендикулярны друг другу. Затем мы каким-то образом добавим в
четвертый (красный):
Итак, у нас есть 4 измерения по 2 грани в каждой = 8 граней.
грани вместе образуют «поверхность» (на самом деле трехмерный объем) размером 8xL 3 в объеме. Рисование изображения четырехмерного тессеракта в трехмерном
размерное пространство прямолинейно.
Мы берем два его лица — два
кубики — и соедините углы.
Есть несколько способов сделать рисунок, который
соответствует взгляду на тессеракт под разными углами. Фигура
показывает два способа сделать это. Первый дает косой обзор; второй
смотрит по одной из осей.
Итак, теперь мы, кажется, знаем все, что нужно знать о тессеракт! Мы знаем его объем в четырехмерном пространстве, как он выражается вместе из восьми кубов как поверхностей и даже каков объем его поверхность (8xL 3 ).
Стереовидение
«Чертежи» тессеракта плохо видны.
Это потому, что они действительно должны быть трехмерными моделями в
трехмерное пространство. Итак, что у нас есть выше, это два
объемный
чертежи трехмерных моделей четырехмерного
тессеракт. Неудивительно, что он становится грязным!
Изображения ниже представляют собой стереопары. Если вы знакомы
с тем, как их просматривать, вы увидите, что они дают вам хороший стереофонический вид
трехмерной модели.
Если это новое для вас, они берут
практика, чтобы увидеть. Вам нужно расслабить свой взгляд, пока ваш левый глаз не смотрит на
левое изображение и правый глаз смотрит на правое изображение.
Но как научиться этому? мне проще всего
начать, если я сижу далеко от экрана и смотрю вдаль
над верхней частью экрана. Я вижу два несколько размытых изображения на
край моего поля зрения. Пока я не сосредотачиваюсь на них, они начинают
дрейфовать вместе. Это то движение, которое вам нужно. Чем больше они дрейфуют
вместе тем лучше. Я стараюсь усилить дрейф, насколько это возможно, пока
осторожно перемещая свой взгляд к изображениям. Цель состоит в том, чтобы получить два
изображения для слияния. Когда они это делают, я продолжаю смотреть на объединенные изображения,
улучшается фокусировка и появляется полный трехмерный стереоэффект
резко. Эффект поразителен и стоит небольших усилий.
Эту пару легче сплавить:
и этот немного сложнее:
Сводная таблица
Мы можем подытожить развитие свойств
tesseract следующим образом:
| Размер | Фигурка | Лицо | Том | Номер лиц | Том поверхность/периметр |
|---|---|---|---|---|---|
| 1 | интервал | точка | л | 1×2=2 | два очки |
| 2 | квадрат | интервал | л 2 | 2×2=4 | 4 л |
| 3 | куб | квадрат | л 3 | 3×2=6 | 6 л 2 |
| 4 | тессеракт | куб | л 4 | 4×2=8 | 8 л 3 |
Вместительный вызов
Если бы вы жили в тессеракте, вы могли бы выбрать
жить на своей трехмерной поверхности, как двухмерный человек
могли бы выбрать жить в 6 квадратных комнатах, которые образуют двухмерный
поверхность куба.
Таким образом, ваш дом будет состоять из восьми кубов, образующих поверхность.
из тессеракта. Представьте себе, что есть двери, где когда-либо две из
эти кубики встречаются. Если вы находитесь в одной из этих комнат, сколько дверей будет
Понимаете? Как бы выглядела следующая комната, если бы вы прошли через одну из
двери? Через сколько дверей нужно пройти, чтобы добраться до самой дальней
комната? Сколько путей ведут в эту самую дальнюю комнату? Можете ли вы иметь какие-либо
окна снаружи тессеракта? Как насчет окон внутрь?
тессеракт?
Некоторые из этих вопросов непростые. Чтобы ответить на них, перейдите вернемся к простому случаю трехмерного куба с гранями, состоящими из квадраты. Задайте аналогичные вопросы там и просто экстраполируйте ответы на тессеракт.
Запутанный вызов
Доступ к четвертому измерению делает возможным многое
иначе это было бы совершенно невозможно. Чтобы увидеть, как это работает, мы будем использовать
стратегия обдумывания процесса в трехмерном пространстве.
Затем
мы воспроизвели его в четырехмерном пространстве.
Рассмотрим монету, лежащую в рамке на столе.
Монета не может быть удалена из рамки в пределах ограничивает двумерную поверхность стола. Теперь вспомните что у нас есть доступ к третьему измерению. Монета легко удалить, просто подняв его в третье измерение, высота над столом. После этого мы можем передвигать монету по своему усмотрению в более высокую слой, а затем опуститься обратно на столешницу за пределами рамы. |
При подъеме следует обратить внимание на то, что движение
вообще не двигает монету в двух горизонтальных направлениях двух
объемное пространство. Таким образом, движение никогда не приближает его к кадру и там
нет опасности столкновения с рамой.
| Теперь повторите этот анализ для его аналог в одном более высоком измерении, мрамор запертым в трехмерном ящике. |
| |
| Теперь, наконец, рассмотрим два зацепленных колец в некотором трехмерном пространстве. Можем мы разделить их, используя доступ к четвертому измерению? |
Это можно сделать точно так же
процесс подъема одного из колец в четвертое измерение. Как
прежде обратите внимание, что подъем не перемещает кольцо ни в одном из
три направления трехмерного пространства, удерживающие
первоначально связанные кольца. Так что движения рисков нет
столкновения перемещаемого кольца с другим. Подъем просто
поднимает перемещенное кольцо на новый трехмерный слой из четырех
размерное пространство, в котором нет ни одной части другого кольца. перемещенное кольцо может быть свободно перемещено в этот новый слой, и если мы
с удовольствием опустился обратно в исходное трехмерное пространство в
совсем другое место. |
А теперь самое сложное. Мы знакомы в нашем трехмерное пространство с завязыванием узлов на веревке. Некоторые узлы просто кажущиеся клубки, которые могут довольно легко разойтись. Остальные настоящие и можно расстегнуть, только продев конец веревки в петлю. Так примите это за настоящий узел: тот, который не может быть развязаны любыми манипуляциями с веревкой, если мы не сможем ухватиться за заканчивается. (Представьте, если хотите, что каждый из них прикреплен к стене и нельзя удалить.)
Задача состоит в том, чтобы убедить
сами понимаете, что в четырехмерном пространстве на веревках нет настоящих узлов.
космос. Основная помощь, которая вам понадобится, — это описанная выше манипуляция с
связанные кольца.
Для начала представьте, как бы вы использовали четвертый
измерение, чтобы развязать какой-нибудь простой узел, который вы легко можете себе представить.
Использование цветов для визуализации дополнительных размер
Общая идея «поднятия» объекта в четвертое измерение все еще кажется неуловимым? Если да, то вот техника для визуализация этого может просто помочь. Хитрость заключается в том, чтобы представить, что различия в положении в дополнительном измерении пространства может быть представлено различия цветов.
Вот как это работает, когда мы начинаем с двухмерного пространства и подняться в третье измерение. Объекты в оригинале два мерное пространство черное. Когда мы поднимаемся через третий измерения, они последовательно приобретают синий цвет, зеленый и красный. |
Теперь давайте применим этот цветной слой. трюк к более раннему примеру подъема монеты из рамки.
монета начинается в том же двухмерном пространстве, что и рамка. Мы поднимаем
это в третье измерение в более высокое
пространственный слой, который мы закодировали красным цветом. В этом высшем
слой, монета может свободно перемещаться влево/вправо и вперед/назад без
пересекающие рамку. Мы перемещаем его вправо, пока он не пройдет
над рамой. Затем опускаем обратно вниз снаружи. |
А теперь представьте, что мы не можем
воспринимать третье измерение напрямую. Вот как мы
представить побег монеты. Он начинается внутри кадра в
пространство кадра. Затем он поднимается из рамы в
третье измерение. В этот момент на это указывает призрачный
красная монета. Его пространственное положение слева/справа и
направление вперед/назад не изменилось. Все, что изменилось, это его
высота. Теперь он находится на красном слое высоты. Если мы переместим монету влево
или справа, или спереди и сзади, в этом красном слое уже не
пересекает рамку и может двигаться прямо над ней. мы этого не увидим
однако перемещайтесь по кадру. Насколько нам известно, это будет
просто пройди через это.Движение монеты в этом трехмерном побеге иллюстрируется призрачным красным монета. |
Этот последний анализ монеты в
кадр является шаблоном для работы с
реальный случай шарика, заключенного в трехмерную коробку. Если
шарик движется в любом из трех известных измерений (вверх/вниз,
влево/вправо и вперед/назад), его движение пересекает стены
ящик, и он не может убежать. Итак, мы поднимаем шарик в четвертый
измерение, не меняя своего положения в трех привычных
размеры.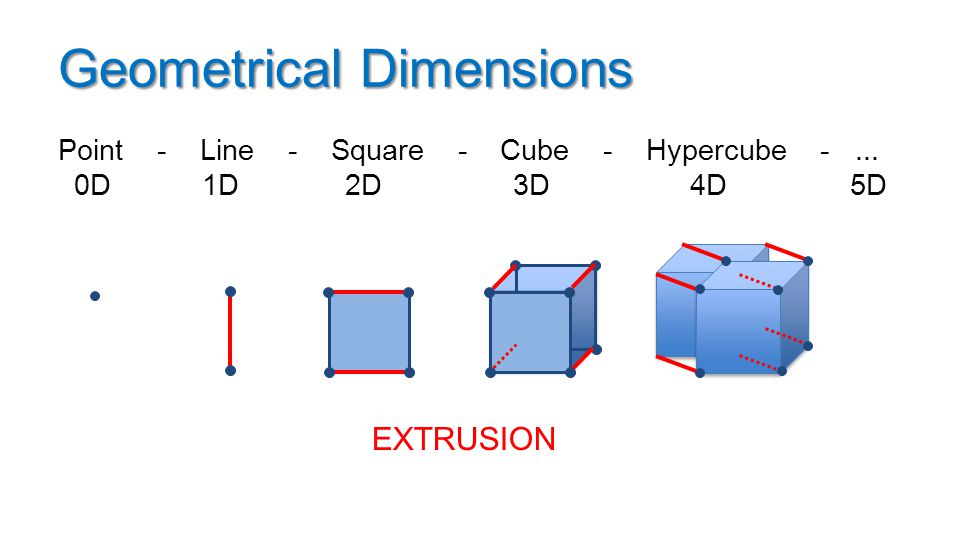 На рисунке это показано тем, что мрамор становится призрачным.
красный. В красном поле шарик может двигаться вверх/вниз,
слева/справа и спереди/сзади, не пересекая стенки коробки.
Затем мрамор перемещается так, что проходит над одной из стен. Это
затем опустили из красного пространства обратно к исходным трем
мерное пространство коробки, но уже вне стен. |
| То же анализ относится к связанным кольцам. Одно кольцо снято из трехмерного пространства исходной установки. В этом красное пространство, кольцо может свободно двигаться, не пересекаясь с другим кольцо. Мы отодвигаем его подальше от другого кольца, а затем опускаем обратно. в исходное трехмерное пространство. Теперь он не связан с другое кольцо. |
Что следует знать
- Свойства квадратов, кубов и тессерактов.
- Как получить свойства тессеракта и других четырехмерные фигуры путем экстраполяции методов, используемых для получения свойства куба.
Авторское право Джон Д. Нортон. февраль 2001 г.;
июль 2006 г., 2 февраля 2008 г.; 6 февраля 2012 г.; 30 апреля 2014. Январь
30, 2022.
Что вам нужно знать о 4-м измерении и технологии 4D
Категории
Новинки
Популярные
Что вам нужно знать о 4-м измерении и технологии 4D
Ожидается, что к настоящему времени почти все пользователи Интернета знакомы с концепцией 3D. Тем не менее, есть новая технология, которая начинает заставлять 3D звучать старее: технология 4D. Что такое 4D-технологии? Стоит ли вообще пытаться с ним познакомиться?
Чтобы помочь вам лучше понять эту технологию, ниже обсуждаются некоторые из наиболее важных моментов, которые вы должны знать о технологии 4D.
- 4D — это не просто обновленное 3D, и мы, вероятно, не можем его воспринимать.
.jpg)
Во-первых, переход от 3D к 4D не похож на переход от 3G к 4G. 4D — это не просто улучшенное 3D. Это совершенно другая область. Хотя можно сказать, что 3D — это 2D с дополнительным измерением, а 4D — это 3D с еще одним измерением, эти геометрические пространства полностью отличаются друг от друга.
Эту разницу можно выделить при восприятии. Говорят, что 2D существа не могут воспринимать 3D, а 3D существа (люди и другие живые существа) не могут воспринимать 4D. 3D существа могут воспринимать 2D, но не могут воспринимать 4D. Вот почему мы находим невозможным или очень трудным визуализировать 4D, хотя некоторые математически подготовленные люди утверждают, что могут это сделать.
Изображение предоставлено: JasonHise через Викисклад. Было бы неправильно говорить, что объекты в 4D-мире анимированы так же, как анимированное изображение выше. Прямо сейчас никто не может точно дать четкое и точное описание того, как выглядит 4D-объект. Возможно, это действительно невозможно.
Есть предположения, что четвертым измерением в 4D является время, что демонстрируется континуумом Минковского, называемым пространством-временем. Однако это только усложняет визуализацию 4D. Что ж, если вы можете визуализировать время, возможно, вы сможете его визуализировать.
Короче говоря, 4D находится в совершенно другом мире. Это похоже на окружающий нас мир, в котором объекты существуют на противоположных сторонах одновременно и (если они разумны) могут видеть все три измерения (длину, ширину и высоту) одновременно, не меняя точки зрения. Это похоже на то, как мы можем видеть 2D-объекты (плоские изображения) во всей их полноте, не меняя точки зрения.
- 4D в настоящее время является просто маркетинговым термином.
4D-кинотеатры, 4D-печать, 4D-тематические парки и другие продукты, рекламируемые как 4D, не являются настоящими четырехмерными творениями. 4D-фильм называется только 4D, поскольку это в основном 3D-фильм (который, кстати, тоже не настоящий 3D, а просто оптическая иллюзия) с добавленными элементами, чтобы сделать просмотр более захватывающим.
Эти элементы включают стробоскопическое освещение, вибрации, дождь, ветер, пузыри и запахи. Точно так же 4D-печать на самом деле создает не 4D-объекты, а объекты, которые могут трансформироваться в ответ на стимул.
Изображение предоставлено Владимиром Соломоновичем через Wikimedia Commons
- 4D-печать не имеет ничего общего с четвертым измерением.
Опять же, 4D-печать — это просто маркетинговый термин. 3D- и 4D-печать на самом деле не так уж сильно отличаются. 4D-распечатки можно создавать с помощью 3D-принтеров. Разница заключается в выходе и используемых материалах. Результатом 4D-печати являются объекты, которые могут самонастраиваться или изменять форму в зависимости от окружающей среды или воздействия раздражителей. Одним из хороших примеров 4D-распечатки является 4D-платье, представленное ранее в этом блоге.
- Ожидается, что коммерциализация 4D-печати произойдет в 2019 году.
Согласно недавнему отчету Research and Markets, 4D-печать может быть коммерциализирована уже к 2019 году.
к 2019 году она станет отраслью с оборотом в 63 миллиона долларов, а к 2025 году — около 500 миллиардов долларов. Индустрия 4D-печати будет состоять из различных сегментов материалов, а именно программируемого древесного волокна, программируемого углеродного волокна и программируемого текстиля. Программируемое углеродное волокно станет крупнейшим сегментом с предполагаемой долей не более 62% рынка 4D-печати.
- 4D-печать в основном определяет время как четвертое измерение.
Мы уже знаем, что 3D означает длину, ширину и высоту, а 4D — это 3D плюс четвертое измерение. Однако четвертое измерение остается спорным. Нет единого мнения, что это такое на самом деле. Однако когда дело доходит до 4D-печати, четвертым измерением является время. Если вам все еще трудно понять, как результат 4D-печати можно назвать 4D-объектом, просто помните, что это 3D + время или 3D-объект, который меняет свою форму с течением времени (или после введения какого-либо стимула).