Подготовка к алгоритмическому собеседованию — бесплатный курс — Яндекс Практикум
Без жёстких дедлайнов — можно проходить в своём темпе
Примеры реальных задач с собеседований
Личный опыт авторов курса
Опытным разработчикам, которые ещё не изучали алгоритмы
Курс позволит не потеряться в обилии фактов. В нём мы собрали то, что нужно изучать для подготовки к собеседованиям.
Разработчикам, которые уже знакомы с алгоритмами и структурами данных
Курс поможет оценить уровень вашей подготовки и сфокусироваться на том, что пригодится на интервью.
Поймёте структуру алгоритмических собеседований, требования и критерии оценки
Проверите свой уровень знаний алгоритмов и структур данных
Попрактикуетесь на реальных задачах с собеседований
Узнаете, как проводятся собеседования и как их успешно проходить
Повторите нужную теорию и проверите свои знания
Потренируетесь решать задачи
Блок 1
Начало
Блок 2
Как проходят алгоритмические собеседования
Блок 3
Какие алгоритмы нужно знать
Блок 4
Какие структуры данных нужно знать
Блок 5
Подготовка и практика
Примеры с кодом написаны на C++ и Python
А практические задачи можно сдавать ещё и на Java
или JavaScript. Для прохождения курса пригодятся знания одного из языков.
Для прохождения курса пригодятся знания одного из языков.
Нет дедлайнов и команды сопровождения
Это курс для самостоятельного изучения. Здесь нет наставников и ревью кода.
Подойдёт ли мне этот курс?
Курс предназначен для разработчиков, которые планируют проходить алгоритмические собеседования. Материалы будут полезны разработчикам независимо от уровня алгоритмической подготовки.
Достаточно ли курса для того, чтобы с нуля разобраться в алгоритмах и структурах данных?
К сожалению, нет. Курс помогает самостоятельно подготовиться к алгоритмическому собеседованию. Если хотите подробнее разобраться в теории алгоритмов и структур данных, присмотритесь к платному курсу «Алгоритмы и структуры данных».
Какие навыки и знания нужны, чтобы пройти курс?
Примеры с кодом написаны на C++ и Python. Сдавать задачи можно также на Java или JavaScript. Студенту нужно знать один из этих четырёх языков.
Как и когда я буду учиться?
В отличие от других курсов Практикума, здесь нет дедлайнов, сопровождения и ревью кода.
Смогу ли я пройти алгоритмическое собеседование после курса?
Знания из курса повысят ваши шансы на успешное прохождение собеседований. В курсе мы сфокусировались на том, что нужно для подготовки к собеседованиям, а также поделились опытом разработчиков и подсветили много неочевидных моментов. А ещё собрали список материалов для самостоятельной подготовки.
Получу ли я какой-то документ после курса?
| 1 |
2 июля 2007 |
«Версия 7» (новая формула ранжирования, повышение числа факторов, анонс состоялся только на searchengines.guru/showthread.php?t=149644). |
|---|---|---|
| 2 |
20 декабря 2007, 17 января 2008 |
«Версия 8» и «Восьмерка SP1». |
| 3 |
16 мая, 2 июля 2008 |
Магадан (Fast Rank для быстрого подбора претендентов, мягкость, расширение базы аббревиатур и синонимов, расширенные классификаторы документов), Магадан 2.0 (уникальность контента, новые классификаторы запросов пользователей и документов). |
| 4 |
11 сентября 2008 |
Находка (учёт стоп-слов в поисковом запросе, новый подход к машинному обучению, тезаурус). |
| 5 |
10 апреля, 24 июня, 20 августа, 31 августа, 23 сентября, 28 сентября 2009 |
Арзамас / Анадырь (учёт региона пользователя, снятие омонимии), Арзамас 1. |
| 6 |
17 ноября 2009 |
Снежинск (запуск технологии машинного обучения MatrixNet, кратный рост числа факторов ранжирования, 19 локальных формул для крупнейших регионов России, сильнейшие изменения выдачи). |
| 7 |
22 декабря 2009, 10 марта 2010 |
Конаково (неофициальное название, но далее будет именно Обнинск, свои формулы для 1250 городов по всей России), Конаково 1.1 (Снежинск 1. |
| 8 | 13 сентября 2010 |
Обнинск (перенастройка формулы, повышение производительности, новые факторы и ранжирование для геонезависимых запросов, доля которых в потоке составляет более 70%). |
| 9 |
15 декабря 2010 |
Краснодар (технология «Спектр» и повышение разнообразия выдачи, разложение запроса пользователя на интенты), далее: повышение локализации выдачи по геозависимым запросам, независимые формулы для 1250 городов России. |
| 10 |
17 августа 2011 |
Рейкьявик (учёт языковых предпочтений пользователей, первый шаг персонализации выдачи). |
| 11 |
12 декабря 2012 |
Калининград (существенная персонализация выдачи: подсказки, учёт долгосрочных интересов пользователя, повышение релевантности для «любимых» сайтов). |
| 12 | 30 мая 2013 |
Дублин (дальнейшая персонализация выдачи: учёт сиюминутных интересов пользователей, подстройка результатов выдачи под пользователя прямо во время поисковой сессии). |
| 13 |
12 марта 2014 |
Началово* «Без ссылок» (отмена учета ссылок / ряда ссылочных факторов в ранжировании для групп коммерческих запросов в Московском регионе). |
| 14 |
5 июня 2014 |
Одесса* «Острова» (новый «островной» дизайн выдачи и сервисов, внедрение интерактивных ответов, в дальнейшем эксперимент были признан неуспешным и завершен). |
| 15 |
1 апреля 2015 |
Амстердам* «Объектный ответ» (дополнительная карточка с общей информацией о предмете запроса справа от результатов выдачи, Яндекс классифицировал и хранит в базе десятки миллионов различных объектов поиска). |
| 16 |
|
Минусинск (понижение в ранжировании сайтов с избыточным числом и долей SEO-ссылок в ссылочном профиле, массовое снятие SEO-ссылок, дальнейшее возвращение учёта ссылочных факторов в ранжировании по всем запросам в Московском регионе). |
| 17 |
14 сентября 2015 (± 3 месяца) |
Киров* «Многорукие Бандиты Яндекса» (рандомизированная добавка к численному значению релевантности ряда документов с оценкой «Rel+», с целью сбора дополнительной поведенческой информации в Московском регионе, в дальнейшем — рандомизация была внедрена и в регионах России). |
| 18 |
2 февраля 2016 |
Владивосток (учёт адаптированности сайта к просмотру с переносных устройств, повышение в результатах мобильной выдачи адаптированных проектов). |
| 19 |
2 ноября 2016 |
Палех (соответствие поисковому запросу семантического вектора в трёхсотмерном пространстве с целью определения близости данного вектора к заголовкам (Title) проиндексированных документов в сети; алгоритм вычисления соответствия пары запрос-документ основан на искусственной нейронной сети; основная цель — повышение качества поиска для редких запросов и запросов, заданных на естественном языке). |
| 20 |
23 марта 2017 |
Баден-Баден (алгоритм определения переоптимизированных текстов, ранее переоптимизированные тексты пессимизировались с помощью текстовых пост-фильтров, теперь поисковая система дополнительно встроила в основной алгоритм ряд факторов, которые ответственны за понижение документов с данными текстами в результатах выдачи). |
| 21 |
22 августа 2017 |
Королёв (алгоритм ранжирования, который является логическим развитием «Палеха»; основная особенность подхода — выявление смысла пользовательского запроса и сопоставление его с теми интентам, которые могут быть удовлетворены на странице; в отличии от «Палеха» — для вычисления новых факторов анализируется весь текст документа, а не только заголовок окна браузера Title). |
| 22 |
19 ноября 2018 |
Андромеда (обновление поиска, которое, формально подытоживает сотни изменений, внедренных со времени анонса алгоритма Королёв; большинство нововведений касаются отображения множества колдунщиков и сервисов Яндекса в SERP; основные изменения — улучшение «быстрых ответов», интеграции с другими сервисами поисковой системы, в том числе — Коллекции, появление значков у сайтов). |
| 23 |
17 декабря 2019 |
Вега (значимое обновление, которое объединяет сразу несколько несвязанных направлений; 1. разбивка базы хранения документов по смысловым кластерам с целью ускорения поиска и повышения полноты индексации, рост объема базы в 2 раза; 2. пререндеринг SERP по запросу, который, с большой вероятностью будет задан пользователем, цель — ускорение отрисовки результатов; 3. внедрение экспертности в оценках асессоров с целью повышения качества выдачи по тематикам, где пользователю особенно важен экспертный контент; 4. гиперлокальность поиска и учёт местоположения пользователя не только на уровне города, но и на уровне района). |
| 23 |
Сентябрь-ноябрь 2020 года |
YATI или Yet Another Transformer (with Improvements). Суть алгоритма состоит в применении тяжелых нейросетей для «поиска по смыслу». Механика схожа с проектом BERT от Google (2018 год запуска). По заверению сотрудников поисковой системы — запуск принёс рекордное улучшение в ранжировании за последние 10 лет (с момента запуска MatrixNet и алгоритма Снежинск, см. выше). |
| 24 |
10 июня 2021 года |
Y1. Новая версия, которая объединяет 2 000+ улучшений, которые внедрялись на протяжении нескольких месяцев. Основа: технология нейросетей-трансформеров и алгоритмы YATI и YALM. YALM — языковая модель, способная генерировать тексты в заданной стилистике. Основные возможности: быстрые ответы (более число), поиск внутри видео, оценка сайтов и бизнесов по отзывам, визуальный поиск, повышение безопасности. Языковые модели и ранее использовались в поиске. YALM просто более мощная версия, способная быстро обучаться и учитывать стилистику на нескольких примерах. |
Algorithm sample problems
Algorithm sample problems
A. Time Through The Glass
Solve this problem at Yandex.Contest
Statement| Time limit | 1 second |
| Memory limit | 512Mb |
| Ввод | стандартный ввод или ввод.txt |
| Вывод | стандартный вывод или вывод.txt |
Бомбослав работает в хорошем и красивом офисе. Весь офис украшен стильными дизайнерскими часами. Их лицо представляет собой стандартную окружность с 60 равноудаленными отметками вдоль нее, которые обозначают минуты. 12 из этих 60 отметок больше остальных (начиная с самой верхней, равноудаленные с шагом в пять отметок), эти отметки обозначают часы. Часы стильные тем, что на них вообще не написаны цифры, автор полагал, что всем известно их местонахождение и какая отметка соответствует какому значению.
Часы стильные тем, что на них вообще не написаны цифры, автор полагал, что всем известно их местонахождение и какая отметка соответствует какому значению.
Сегодня кто-то повесил эти часы над рабочим местом Бомбослава. Он проверил их несколько раз и заметил, что их поведение какое-то странное. Приглядевшись, он понял, что на самом деле смотрит в зеркало, в котором отражаются часы, расположенные позади него. Это означает, что циферблат часов отражается вдоль вертикальной линии, проходящей через центр циферблата. Теперь он хочет иметь возможность определять текущее время, зная время в зеркальной версии часов.
Часы сделаны таким образом, что движение обеих стрелок дискретно , т. е. часовая стрелка всегда указывает на одну из 12 больших отметок, показывающих текущий час, а минутная стрелка всегда указывает на одну из 60 отметок, показывающих текущий час. минута.
Формат ввода
Единственная строка входных данных содержит два целых числа h и m(0≤h≤11, 0≤m≤59) — текущее положение часовой стрелки и текущее положение минутной стрелки в отраженной версии часов. ч=0 означает, что часовая стрелка указывает вверх, ч=3 обозначает позицию, указывающую вправо, ч=6 — вниз и ч=9- Слева. То же самое относится к минутной стрелке и значениям м=0, м=15, м=30 и м=45
ч=0 означает, что часовая стрелка указывает вверх, ч=3 обозначает позицию, указывающую вправо, ч=6 — вниз и ч=9- Слева. То же самое относится к минутной стрелке и значениям м=0, м=15, м=30 и м=45
Формат вывода
Выведите два целых числа x и y(0≤x≤11, 0≤y≤59) — фактическое время, отображаемое на часах.
Образец 1
Образец 2
Примечания
На рисунке ниже показан первый образец. Левые часы показывают то, что видит Бомбослав, а правые часы обозначают исходное положение стрелок часов. Часовая стрелка красная, а минутная — синяя.
РешениеРешение
Рассмотрим движение «реальной» и «отраженной» рук. Если «настоящая» рука поворачивается на некоторый угол, то «отраженная» рука проходит точно такой же угол в другом направлении. Таким образом, сумма углов двух стрелок всегда равна 360 градусам. Для каждой руки мы найдем ее результирующую позицию независимо. Для часовой стрелки это 12 минус текущая позиция, а для минутной стрелки 60 минус текущая позиция. В обоих случаях мы не должны забывать заменить 12 или 60 на 0,9.0009
В обоих случаях мы не должны забывать заменить 12 или 60 на 0,9.0009
B. Palindromic Feature
Solve this problem at Yandex.Contest
Statement| Time limit | 1 second |
| Memory limit | 512Mb |
| Input | standard input or input .txt |
| Вывод | стандартный вывод или output.txt |
Аркадий очень любит машинное обучение, он пытается применять его в каждой задаче, над которой работает. Он верит в невероятную магическую силу этой популярной молодой части компьютерных наук. Вот почему Аркадий всегда изобретает новые функции машинного обучения, чтобы вычислять их для своих любимых объектов.
Напомним, что строка называется палиндром , если она читается одинаково с начала до конца и наоборот, с конца в начало. Для каждой строки в своей базе данных Аркадий хочет вычислить ее кратчайшую подстроку , которая состоит как минимум из двух символов и является палиндромом.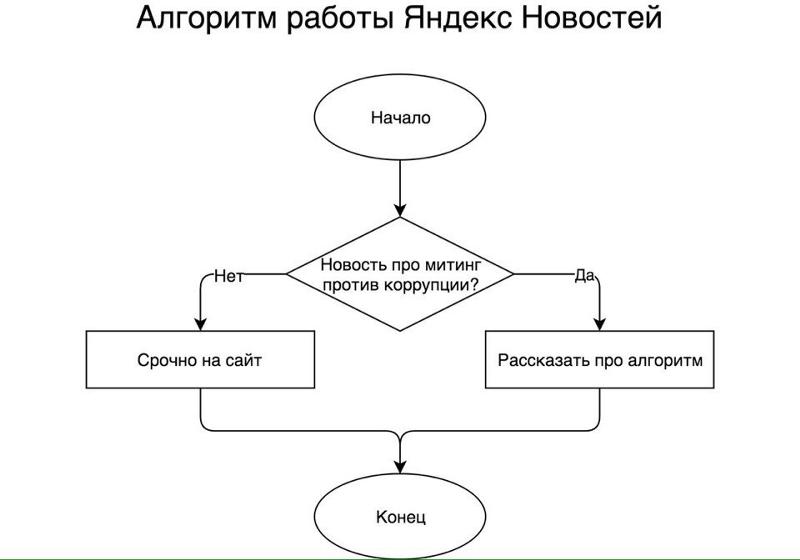 Если таких строк несколько, Arkday хочет выбрать лексикографически наименьшую из них.
Если таких строк несколько, Arkday хочет выбрать лексикографически наименьшую из них.
Формат ввода
Единственная строка входных данных содержит единственную строку из базы данных Аркадия, то есть непустую последовательность строчных латинских букв. Длина этой строки не менее 2 и не превышает 200 000 символов.
Формат вывода
Выведите кратчайшую подстроку входной строки, состоящую не менее чем из двух символов и являющуюся палиндромом. Не забывайте, что Аркадий хочет найти лексикографически наименьшую возможную такую строку.
Образец 1
Образец 2
Примечания
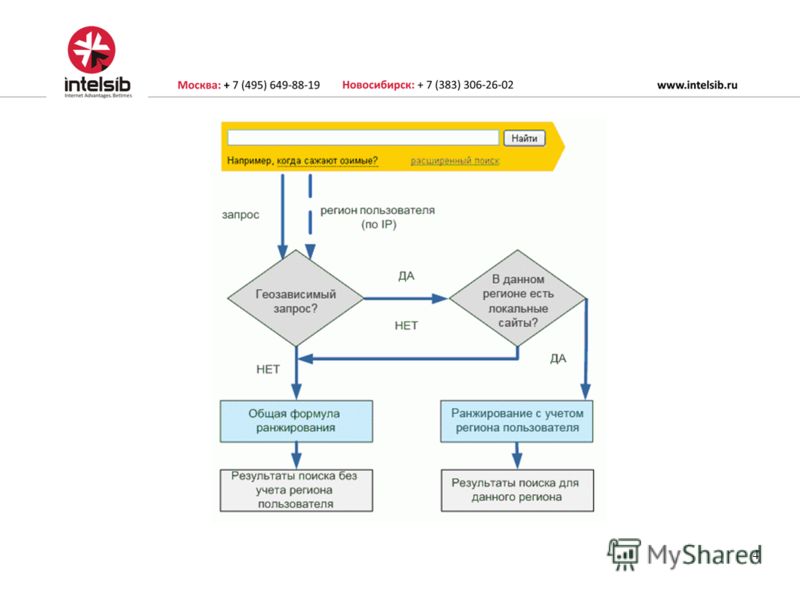
Мы говорим, что строка а=а1а2 … ан) лексикографически меньше, чем строка b=b1b2 … bm) если верно одно из следующих утверждений:
- если nm и a1=b1, a2=b2, …, an=bn, то есть первая строка является префиксом второй строки.
- такая позиция существует 1≤i≤min(n,m), что a1=b1, a2=b2 …, ai-1=bi-1 и ai=bi, то есть первая строка имеет меньший символ в первой позиции, где строки отличаются.
Раствор
Рассмотрим некоторую подстроку заданной строки, являющуюся палиндромом. Мы можем удалить ее первый символ и ее последний символ, и строка останется палиндромом. Продолжайте этот процесс, пока длина строки не станет равной двум или трем (в зависимости от четности).
Количество подстрок длины два или три линейно, как и их общая длина. Таким образом, мы можем применить наивный алгоритм для выбора оптимального палиндрома. Если нет палинромной подстроки длины два или три, выведите -1.
C. Divide Them All
Solve this problem at Yandex.Contest
Statement| Time limit | 1 second |
| Memory limit | 512Mb |
| Ввод | стандартный ввод или ввод.txt |
| Вывод | стандартный вывод или вывод.txt |
После тяжелого рабочего дня Оля и Толя решили сходить на стрельбище. Они уже прослушали вводный инструктаж, получили в руки винтовки и теперь стоят на огневых позициях. Через них проходит стена, на которой расположены n мишеней. Каждая мишень может рассматриваться как фигура на плоскости и представляет собой либо круг, либо прямоугольник. Цели могут перекрываться и пересекаться любым образом.
Они уже прослушали вводный инструктаж, получили в руки винтовки и теперь стоят на огневых позициях. Через них проходит стена, на которой расположены n мишеней. Каждая мишень может рассматриваться как фигура на плоскости и представляет собой либо круг, либо прямоугольник. Цели могут перекрываться и пересекаться любым образом.
Перед началом стрельбы Оля и Толя решили провести линию, которая разделит самолет со всеми мишенями на две части, чтобы можно было идентифицировать выстрелы. Однако для справедливости они хотят, чтобы эта линия делила каждую из мишеней на две равные части. То есть для каждого круга и каждого прямоугольника линия должна делить эту фигуру на две равные по площади части.
Оля и Толя долго спорили, чтобы придумать этот план разделения. Однако они не уверены, что такая линия вообще существует, и просят вас проверить, возможно ли желаемое деление или нет.
Формат ввода
Первая строка ввода содержит одно целое число n(1≤n≤100 000) количество целей.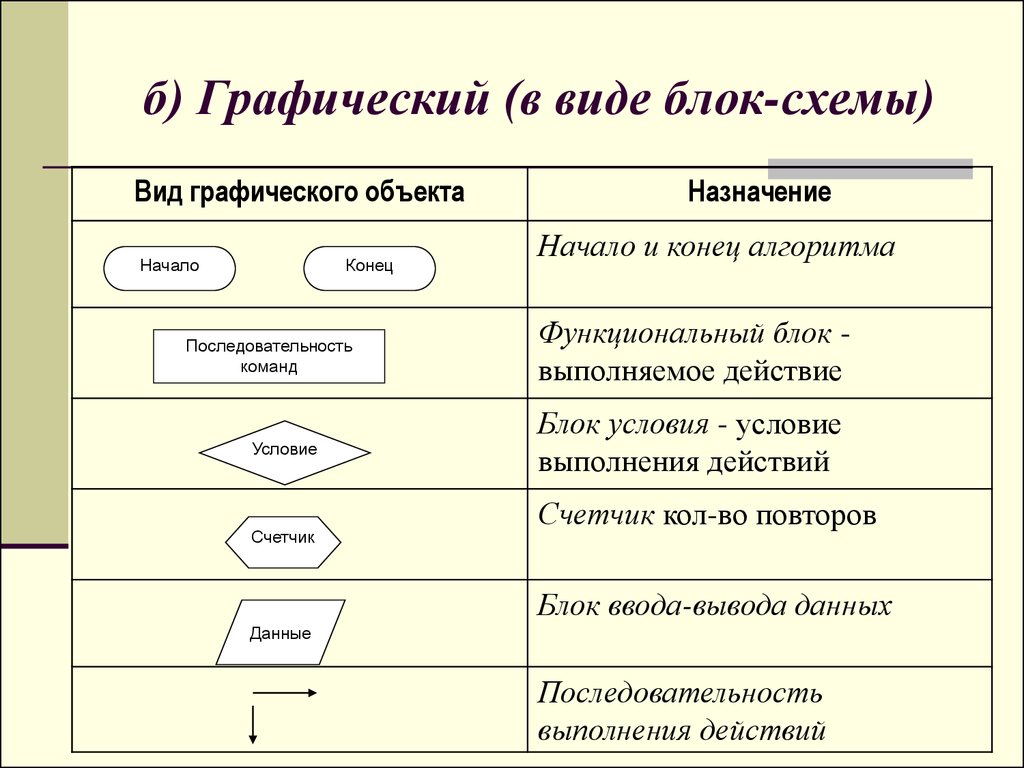 Каждая из следующих n строк начинается с целого числа ти(0≤ти≤1), которые определяют тип этой цели.
ти=0, означает, что эта цель представляет собой круг и еще три целых числа ри, xi и yi, следовать (1≤ri≤1000, −10 000≤xi, yi≤10 000) . Они определяют радиус и координаты центра окружности соответственно. Если ти=1, то эта цель представляет собой прямоугольник и определяется еще восемью целыми числами x1,i, y1,i, x2,i, y2,i, x3,i, y3,i, x4,i, y4,i — координаты его вершин в порядке обхода по или против часовой стрелки
(−10 000≤xj,i, yj,i≤10 000). Гарантируется, что данные четыре точки образуют прямоугольник положительной площади.
Каждая из следующих n строк начинается с целого числа ти(0≤ти≤1), которые определяют тип этой цели.
ти=0, означает, что эта цель представляет собой круг и еще три целых числа ри, xi и yi, следовать (1≤ri≤1000, −10 000≤xi, yi≤10 000) . Они определяют радиус и координаты центра окружности соответственно. Если ти=1, то эта цель представляет собой прямоугольник и определяется еще восемью целыми числами x1,i, y1,i, x2,i, y2,i, x3,i, y3,i, x4,i, y4,i — координаты его вершин в порядке обхода по или против часовой стрелки
(−10 000≤xj,i, yj,i≤10 000). Гарантируется, что данные четыре точки образуют прямоугольник положительной площади.
Формат вывода
Если существует линия, которая делит каждую из целей на две части равной площади, выведите «Да» . в единственной строке вывода. В противном случае напечатайте «Нет» .
Образец 1
Образец 2
Образец 3
РешениеРешение
Для решения этой задачи воспользуемся простым геометрическим фактом, что линия делит окружность на две части равной площади тогда и только тогда, когда эта линия проходит через центр окружности. Точно так же прямая делит прямоугольник на две части равной площади тогда и только тогда, когда она проходит через точку пересечения его диагоналей. В обоих случаях достаточность следует из точечной симметрии, а необходимость можно показать, рассмотрев прямую, проходящую через центр и параллельную данной.
Точно так же прямая делит прямоугольник на две части равной площади тогда и только тогда, когда она проходит через точку пересечения его диагоналей. В обоих случаях достаточность следует из точечной симметрии, а необходимость можно показать, рассмотрев прямую, проходящую через центр и параллельную данной.
Теперь нам нужно только проверить, существует ли линия, содержащая все центры. Ради простоты мы будем работать с удвоенными координатами, чтобы они оставались целыми. Это позволяет нам получить центр прямоугольника, вычислив сумму координат двух противоположных вершин.
Если среди множества всех центров не более двух различных точек, то ответ однозначно положительный. В противном случае рассмотрите любую пару различных точек и убедитесь, что каждый центр принадлежит линии, которую они определяют. Чтобы проверить, являются ли три точки а, б и в (а≠б) принадлежат одной прямой, мы можем вычислить векторное произведение векторов б-а и с-а. Общая сложность этого решения На).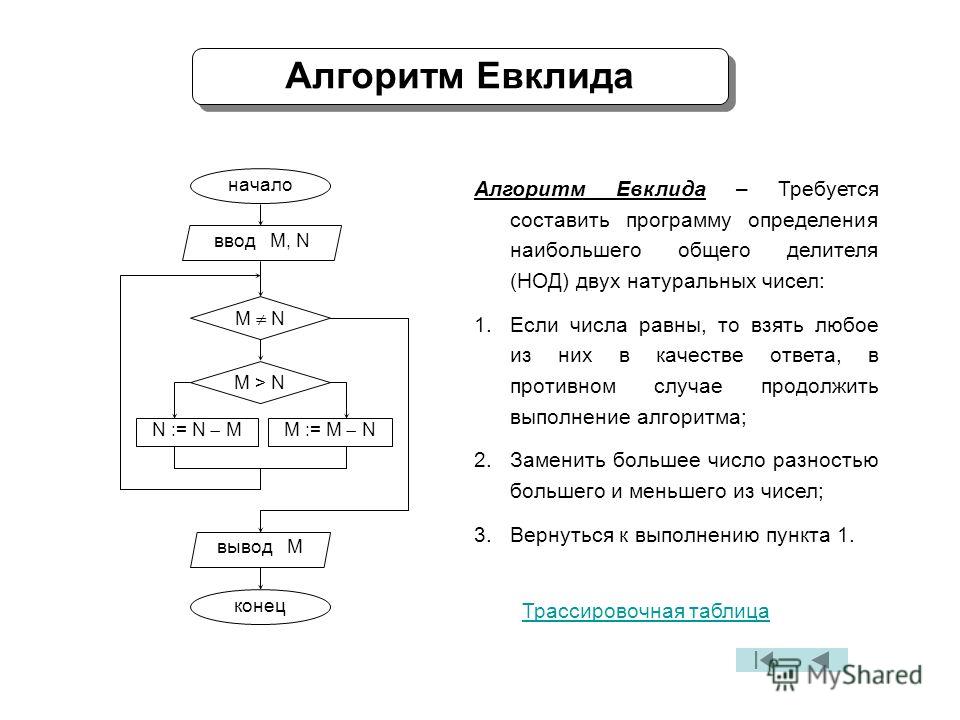
D. Interview Task
Solve this problem at Yandex.Contest
Statement| Time limit | 3 seconds |
| Memory limit | 512Mb |
| Input | standard input or input .txt |
| Вывод | стандартный вывод или output.txt |
Алексей очень опытный интервьюер. Несмотря на то, что он дал несколько сотен собеседований на стажировку, он чувствует, что пора что-то менять. Кандидаты теперь легко решают все замечательные задачи, которыми он успешно пользовался все эти годы.
Выбора нет, поэтому Алексей придумал новое задание. Вам дана последовательность целых чисел, которая на первом шаге состоит из двух целых чисел 1. На каждом шаге вы вставляете новый элемент между любыми двумя соседними элементами последовательности, и значение нового элемента равно их сумме. После нескольких первых шагов последовательность выглядит следующим образом:
• 1 1
• 1 2 1
• 1 3 2 3 1
• 1 4 3 5 2 5 3 4 1
Во время собеседования Алексей планирует попросить кандидата написать программу, которая по заданному целочисленному значению n будет вычислять, сколько раз значение n встречается в последовательности на шаге n. Хотя Алексей понятия не имеет, как решить эту задачу, он слышал, что следующий кандидат — опытный участник соревнований по программированию, поэтому он должен придумать решение.
Хотя Алексей понятия не имеет, как решить эту задачу, он слышал, что следующий кандидат — опытный участник соревнований по программированию, поэтому он должен придумать решение.
Формат ввода
Ввод состоит из одного целого числа n(1≤n≤1013).
Формат вывода
Выведите одно целое число, сколько раз целое число n встречается в последовательности на шаге n.
Образец 1
Образец 2
РешениеРешение
Мы хотели бы начать с некоторых лемм.
Лемма 1 . Любые два соседних целых числа взаимно просты на любом шаге.
Используйте математическую индукцию. Базовый случай тривиален, так как 1 и 1 взаимно просты. Предположим, что утверждение верно для первых n шагов. Затем любое целое число, полученное на шаге п+1 представляет собой сумму двух взаимно простых чисел. Однако, НОД(а+b, b)=НОД(a, b), таким образом, любые два соседа по-прежнему взаимно просты.
Лемма 2 . Каждая упорядоченная пара целых чисел (а, б) появляется в качестве соседей ровно один раз (и только на одном шаге).
Каждая упорядоченная пара целых чисел (а, б) появляется в качестве соседей ровно один раз (и только на одном шаге).
Доказательство от противного. Пусть k — первый шаг, при котором некоторая упорядоченная пара появилась во второй раз. Обозначим эту пару как (р, q) и я≤к это шаг другого появления этой пары. Без ограничения общности пусть р>q , то p было получено как сумма p-q и q, таким образом, на шагах я-1 и к-1 также имело место повторение какой-либо пары, порождающее противоречие.
Лемма 3 . Любая упорядоченная пара взаимно простых чисел встретится на каком-то шаге.
Пусть p и q соседи на каком-то шаге. Тогда, если
р>q он был получен как сумма
p-q и q, значит, они были соседями на предыдущем шаге. В двух шагах позади нас было либо
р-2q
и q, или
p-q
и
2q-p
(в зависимости от того, что больше,
p-q или q) и так далее. Процесс аналогичен алгоритму Евклида и продолжается, пока у нас нет 1 и x. Наконец, пары (1, х) и (х, 1) всегда появляются на шаге x$.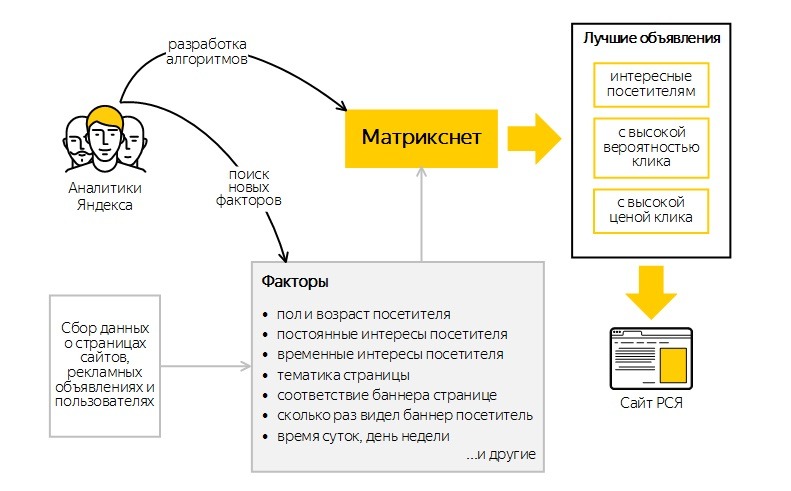 Двигаясь по действиям в обратном направлении, приходим к выводу, что любая из промежуточных пар должна появиться в процессе, таким образом, пара (р, q) также появляется.
Двигаясь по действиям в обратном направлении, приходим к выводу, что любая из промежуточных пар должна появиться в процессе, таким образом, пара (р, q) также появляется.
Вычисление функции Эйлера — хорошо изученная задача. Это известно, что это мультипликативная функция, поэтому n=p1k1·p2k2· … ·pnkn , количество взаимно простых целых чисел равно (p1k1-p1k1-1)·(p2k2-p2k2-1)· … (pnkn-pnkn-1) Факторизация n может быть выполнена в На) время.
E. Backup
Solve this problem at Yandex.Contest
Statement| Time limit | 5 seconds |
| Memory limit | 512Mb |
| Input | standard input or input. txt txt |
| Вывод | стандартный вывод или output.txt |
Чтобы пользовательские данные были в безопасности и не были потеряны при аварии, Аркадий постоянно придумывает и тестирует новые способы организации резервного копирования. На этот раз он перечислил все компьютеры, которыми он владеет, от 1 до n и для каждого компьютера с индексом от 1 до п-1 идентифицированный резервный компьютер Пи Он следовал правилу, согласно которому индекс резервного компьютера всегда должен быть больше индекса самого компьютера, т.е. пи > я . Из-за этого правила нет резервной копии для компьютера n.
Во время текущего эксперимента Аркадий выбрал некоторую конфигурацию значений Пи , и теперь планирует выключать компьютеры в определенном порядке, по одному компьютеру в секунду. Эксперимент заканчивается, когда компьютер с индексом n выключается. Изначально каждый компьютер имеет блок данных размера 1. Когда компьютер x выключается, его блок данных размера 1 копируется на компьютер. пикс. . В случае, если на компьютере x были какие-то другие блоки (которые были получены в качестве резервной копии с других компьютеров) и они не копируются и считаются потерянными. Более того, если компьютер пикс. уже выключен, блок данных с компьютера x никуда не копируется и также считается утерянным.
пикс. . В случае, если на компьютере x были какие-то другие блоки (которые были получены в качестве резервной копии с других компьютеров) и они не копируются и считаются потерянными. Более того, если компьютер пикс. уже выключен, блок данных с компьютера x никуда не копируется и также считается утерянным.
Акради хочет, чтобы его эксперимент длился как можно дольше. Однако он должен следовать еще одному правилу: если в течение какой-то секунды количество блоков данных, собранных на какой-то машине, равно k, то эта машина должна быть выключена в течение следующей секунды для обеспечения аппаратной безопасности. Обратите внимание, что последняя секунда (когда компьютер n выключен) не учитывается.
Формат ввода
Первая строка ввода содержит одно целое число т(1≤т≤20) — количество тестов.
Затем следуйте t описаниям отдельных тестов. Каждое описание начинается с двух целых чисел n и k(1≤n≤100 000, 2≤k≤10). — количество компьютеров, участвующих в этом эксперименте, и максимально возможная загрузка одного компьютера. Следующая строка содержит
п-1 целые числа p1, p2, … pn-1(i+1≤pi≤n) .
Следующая строка содержит
п-1 целые числа p1, p2, … pn-1(i+1≤pi≤n) .
Формат вывода
Для каждого из t тестов выведите одно целое число, равное максимально возможному количеству секунд, прежде чем Аркадию придется выключить машину номер n.
Образец
РешениеРешение
В этой задаче нам дано корневое дерево. За один шаг удаляется один узел. Если узел удаляется, а его непосредственный предок все еще присутствует, значение в этом предке увеличивается на 1 (изначально все значения равны 1). Если значение некоторого узла равно k, его следует удалить на следующем шаге. Цель состоит в том, чтобы максимизировать количество шагов при удалении корня.
Обратите внимание, что если корень имеет только к-1 потомок, мы можем удалить все дерево, прежде чем коснуться узла n. В противном случае потомки должны быть разделены на три множества: полностью удаленные поддеревья, поддеревья с оставшимся корнем и одно поддерево, у которого в конце удаляется корень, вызывающий узел n. также подлежат удалению. Запустите поиск в глубину, чтобы вычислить следующее значение динамического программирования:
также подлежат удалению. Запустите поиск в глубину, чтобы вычислить следующее значение динамического программирования:
средний) это количество узлов, которые мы можем удалить в поддереве v, если нам разрешено удалить v в любой точке. Можно показать, что средний) равно общему количеству узлов в поддереве.
б(в) это количество узлов, которые мы можем удалить в поддереве v, если нам не разрешено касаться узла v. Если их меньше к-1 потомки, б(в) равно а(в)-1 . В противном случае мы должны выбрать к-2 потомок использовать значение а(у) , а для других мы используем б(у) . Этот к-2 потомки выбираются по максимальному значению а(и)-б(и) .
резюме) равно количеству узлов, которые мы можем удалить, если нам разрешено удалить узел v, но это нужно сделать в самом конце. Значение
с (н)
это окончательный ответ. Мы должны выбрать некоторые
к-2
потомки использовать а(у) , один для использования с(и) а для других берем б(у) . Попробуйте каждого потомка как кандидата на с(и) и для другого использования жадный алгоритм, чтобы выбрать лучший
а(и)-б(и) . Предварительно вычислить отсортированный массив всех потомков и вычислить сумму к-2 лучший. Если потомок x будет использоваться с
с(х)
среди них
к-2
использовать к-1
(должно быть как минимум к-1
потомков, иначе уничтожаем все поддерево).
Предварительно вычислить отсортированный массив всех потомков и вычислить сумму к-2 лучший. Если потомок x будет использоваться с
с(х)
среди них
к-2
использовать к-1
(должно быть как минимум к-1
потомков, иначе уничтожаем все поддерево).
Общая сложность О(n log n)
F. Lying Processors
Solve this problem at Yandex.Contest
Statement| Time limit | 3 seconds |
| Memory limit | 512Mb |
| Input | standard input or input .txt |
| Вывод | стандартный вывод или output.txt |
Для тестирования последних достижений в области алгоритмов машинного обучения Евгений использует
н·м процессоры, расположенные в элементарных ячейках п×м доска. Таким образом, процессоры занимают n рядов, по m штук в каждом. Два процессора называются соседними, если они расположены в соседних ячейках одной строки или на одинаковых позициях в соседних строках.
В результате неудачного эксперимента с новым алгоритмом некоторые процессоры научились врать Евгению. Однако, благодаря базовой версии используемого алгоритма, все обработчики, которые научились лгать, делают это каждый раз, когда что-то сообщают Евгению, так что результат их работы по-прежнему легко интерпретировать.
Сейчас Евгений работает над тем, чтобы определить, какие из процессоров всегда лгут, но для начала он хочет понять возможный размер проблемы. Для этого он спросил у каждого из процессоров, правда ли, что среди его соседей есть процессоры, которые работают правильно, и процессоры, которые всегда возвращают ложь? К его удивлению, каждый из процессоров ответил положительно. Теперь Евгений задается вопросом, какое минимально возможное количество лежащих процессоров на плате может привести к таким ответам?
Формат ввода
Единственная строка входных данных содержит два целых числа n и m(1≤n≤7, 1≤m≤100) — количество рядов на плате и количество процессоров в каждом из рядов соответственно.
Формат вывода
Выведите одно целое число — минимально возможное количество лжецов среди процессоров на доске, при котором каждый из процессоров сообщил, что среди его соседей есть как правильные, так и лживые процессоры.
Образец 1
Образец 2
Примечания
Одно из возможных решений в первом примере (лжецы отмечены единицами): 1):
100
001
Решение
Мы будем использовать тот факт, что п≤7 и вычислить профиль динамического программирования. Если мы уже заполнили первые i столбцов таблицы и для первого все верно я-1 столбцы, нам нужно знать только состояние последних столбцов, чтобы иметь возможность продолжить.
Пусть дп(я, м1, м2) , где i варьируется от 1 до m, м1 и
м2 битовые маски в диапазоне от 0 до 2н-1
означает минимальное количество процессоров, необходимое для заполнения первых i столбцов, чтобы сделать первый я-1
столбцы правильные, а последние два столбца должны быть заполнены как м1 и
м2 соответственно. Количество различных состояний равно О(м·22n) . Наконец, чтобы вычислить релаксации, мы пробуем все возможные маски.
м3
для нового государства дп(я+1, м2, м3) .
Количество различных состояний равно О(м·22n) . Наконец, чтобы вычислить релаксации, мы пробуем все возможные маски.
м3
для нового государства дп(я+1, м2, м3) .
Применяя битовые операции и некоторые предварительные вычисления получаем О(м·23n) Продолжительность. Мы можем значительно ускорить его, предварительно вычислив все допустимые значения. м3 за пару (м1, м2) .
Упражнение: придумай О(нм22н) решение.
Онлайн-курсы
Курс «Введение в машинное обучение»
Эта программа охватывает полный цикл анализа данных, от сбора данных до выбора оптимального решения и оценки качества. Вы научитесь использовать современные инструменты аналитики и адаптировать их под конкретные задачи. Каждый курс включает в себя теорию и практические задания разного уровня сложности. На финальном этапе у вас будет возможность разработать собственные проекты для решения любой текущей бизнес-задачи. В результате получится рабочая модель, которую можно использовать на работе или на собеседованиях.
Специализация «Машинное обучение и анализ данных»
Данная программа охватывает полный цикл анализа данных, от сбора данных до выбора оптимального решения и оценки качества. Вы научитесь использовать современные инструменты аналитики и адаптировать их под конкретные задачи. Каждый курс включает в себя теорию и практические задания разного уровня сложности. На финальном этапе у вас будет возможность разработать собственные проекты для решения любой текущей бизнес-задачи. В результате получится рабочая модель, которую можно использовать на работе или на собеседованиях.
Специализация «Большие данные для инженеров»
Эта программа предназначена в первую очередь для тех, кто хочет работать с большими объемами данных. Он охватывает хранение данных и создание отказоустойчивых и эффективных систем обработки. Эта специализация также полезна для интеллектуального анализа данных. Вы попрактикуетесь в использовании современных платформ и инструментов, выполните четыре проекта и поймете, как решать наиболее распространенные проблемы, связанные с большими данными. После прохождения программы вы будете знать, как обрабатывать данные разными способами, использовать методы машинного обучения для больших данных и внедрять эти методы в продукты.
После прохождения программы вы будете знать, как обрабатывать данные разными способами, использовать методы машинного обучения для больших данных и внедрять эти методы в продукты.
Специализация Advanced Machine Learning
Программа фокусируется на глубоком обучении, обучении с подкреплением, автоматической обработке текста, компьютерном зрении и байесовских методах. Вы получите практические навыки решения проблем от победителей конкурса машинного обучения Kaggle и специалистов по данным, работающих в CERN. После прохождения семи курсов вы сможете применять современные методы машинного обучения в своих проектах, понимать, как обрабатывать реальные данные и более эффективно использовать существующие инструменты.
Искусство разработки в современном C++
Эта программа состоит из пяти курсов, каждый из которых длится пять недель. Преподаватели делятся своим многолетним коллективным опытом создания крупных проектов на C++. Они не просто охватывают то, что написано в учебнике, но и учат решать проблемы, с которыми большинство разработчиков сталкиваются на практике.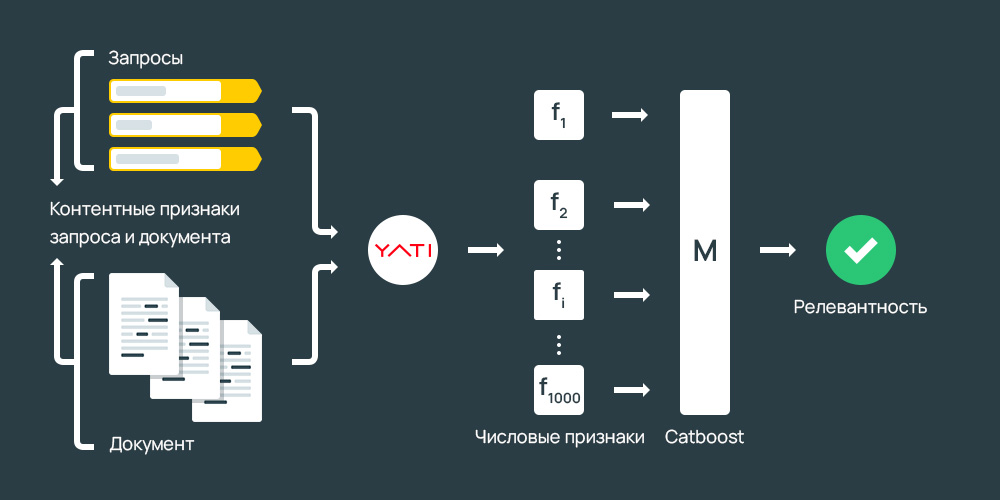

 Авторитетные ресурсы получили значимый плюс в ранжировании, внедрение фильтрации «прогонов» для накрутки ссылочных факторов.
Авторитетные ресурсы получили значимый плюс в ранжировании, внедрение фильтрации «прогонов» для накрутки ссылочных факторов. 1 (новая региональная формула для ряда городов, кроме Москвы, Санкт-Петербурга и Екатеринбурга), Арзамас 1.2 (новый классификатор геозависимости запросов), Арзамас+16 (независимые формулы для 16 регионов России), Арзамас 1.5 (новая общая формула для геонезависимых запросов), Арзамас 1.5 SP1 (улучшенная региональная формула для геозависимых запросов).
1 (новая региональная формула для ряда городов, кроме Москвы, Санкт-Петербурга и Екатеринбурга), Арзамас 1.2 (новый классификатор геозависимости запросов), Арзамас+16 (независимые формулы для 16 регионов России), Арзамас 1.5 (новая общая формула для геонезависимых запросов), Арзамас 1.5 SP1 (улучшенная региональная формула для геозависимых запросов). 1) — обновление формулы для геонезависимых запросов.
1) — обновление формулы для геонезависимых запросов.

 Судя по данным апометра выдачи Яндекса — публичный запуск мог произойти 30 сентября, когда наблюдался существенный излом для динамики показателей: возраст, доля главных страниц, размер документов. Официальный анонс состоялся 25 ноября на конференции YaC 2020.
Судя по данным апометра выдачи Яндекса — публичный запуск мог произойти 30 сентября, когда наблюдался существенный излом для динамики показателей: возраст, доля главных страниц, размер документов. Официальный анонс состоялся 25 ноября на конференции YaC 2020.